Normal Distribution and Confidence Intervals

A confidence interval (CI) gives an “interval estimate” of an unknown population parameter, such as the mean. It gives us the probability that the parameter lies within the stated interval (range). The precision or accuracy of the estimate depends on the width of the interval.

For us to define a \(100(1 – α)%\) confidence interval for \(θ\), we must specify two random variables \(θ_1(X)\) and \(θ_2(X)\) such that \(P(θ_1(X) < θ < θ_2(X)) = 1 – α\).

The most common value for \(α\) is 0.05, which leads us to a 95% confidence interval. As such, \(P(θ_1(X) < θ < θ_2>(X)) = 0.95\) specifies \(θ_1(X)\) and \(θ_2(X)\) such that there is a 95% chance of finding the true value of \(θ\) in the interval. Alternatively, we could say that 5% of the realizations of such intervals would not contain the true value of \(θ\).

The Importance of a Confidence Interval

It is not always possible to know the exact values of the population mean or the population standard deviation. This is because most populations are too large to allow data collection from every subject. In fact, the collection of data from every subject in a large population is not only economically unviable but also very time-consuming. This makes confidence intervals very important.

Confidence intervals can also be used to predict the value of a given parameter. We usually assume that the underlying random variable has a normal distribution. In this regard, the central limit theorem (the assertion that most distributions tend to adopt a normal distribution when n is large) is a very important tool.

The following statements are true for any random variable that assumes a normal distribution:

1. 50% CI: Approximately 50% of all observations fall in the range \(μ ± \left(\frac{2}{3}\right)σ\).
2. 68% CI: Approximately 68.3% of all the observations fall in the range \(μ ± σ\).
3. 95% CI: Approximately 95.5% of all observations fall in the interval \(μ ± 2σ\).
4. 99% CI: Approximately 99.7% of all the observations fall in the interval \(μ ± 3σ\).

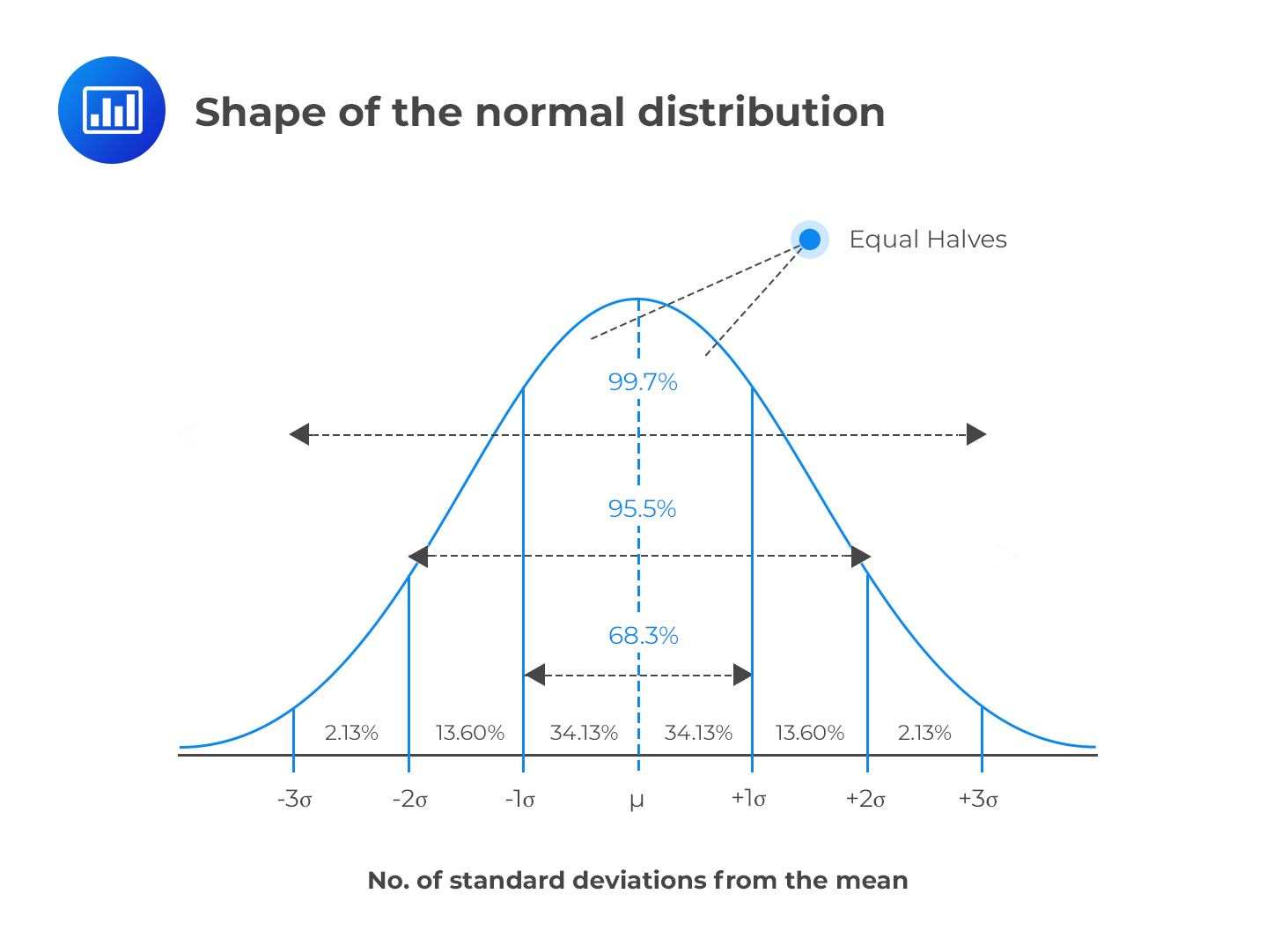
Note to candidates: The words “interval” and “range” have been used interchangeably in this context.

Example: Confidence Interval

A financial analyst encounters a client whose portfolio return has a mean yearly return of 24% and a standard deviation of 5%. Assuming a normal distribution, the 50% confidence interval for the expected return is closest to:

Solution

$$ \begin{align*}
\text{Confidence interval at 50%} & = \left\{ 0.24 – \cfrac {2}{3} \times 0.05, 0.24 + \cfrac {2}{3} \times 0.05 \right\} \\
& = \left\{ 0.207, 0.273 \right\} \\
\end{align*} $$

Question

A financial analyst encounters a client whose portfolio return has a mean yearly return of 24% and a standard deviation of 5%. Assuming a normal distribution, a 99% confidence interval for the expected return is closest to:

1. {0.08, 0.49}.
2. {0.09, 0.39}.
3. {0.09, 0.9}.

Solution

The correct answer is B.

For a 99% CI, approximately 99% of all the observations fall in the interval \(μ ± 3σ\).

Therefore,

$$ \begin{align*} \text{Confidence interval at 99%} & = \left\{ 0.24 – 3 \times 0.05, 0.24 + 3 \times 0.05 \right\} \\
& = \left\{ 0.09, 0.39 \right\} \\
\end{align*} $$

B is incorrect. The calculation assumes a 95% CI:

$$\text{Confidence interval at 95%}=0.24–2×0.05,0.24+2×0.05=\{0.14,0.34\}$$

C is incorrect. The calculation assumes a 68% CI:

$$\text{Confidence interval at 68%}=0.24–0.05,0.24+0.05=\{0.19,0.29\}$$