Principles of Portfolio Construction

Once the IPS containing the investment objectives and investment constraints has been determined along with the risk budget and the classification of asset classes, a portfolio needs to be constructed with the aim of meeting those objectives. The expected returns, standard deviations, and correlations between asset classes can be used to generate an optimal portfolio on a top-down basis. Alternative frameworks for portfolio construction, such as the core-satellite approach, can also be considered.

Optimal Portfolio

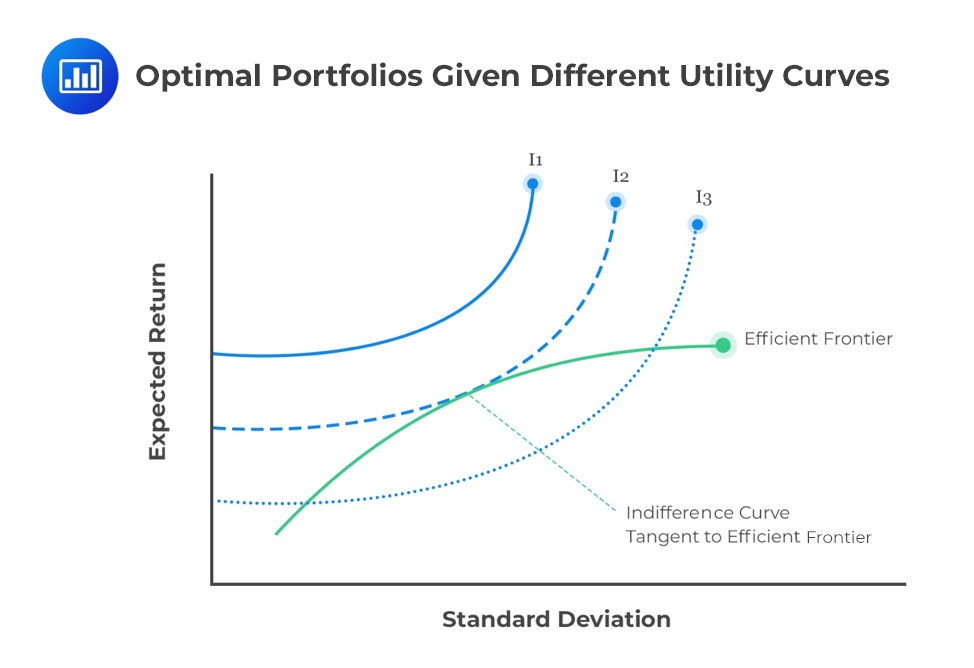
Rational investors will seek to maximize the risk-return tradeoff on their investment portfolio. Their risk-return objectives can be described as a utility function in which utility increases with higher expected returns and lower risk. The portfolio represents a particular asset allocation. The asset allocation that provides the highest expected utility is the one that is optimal for the investor, given their risk aversion.

Capital market expectations specified as the expected returns, standard deviations, and correlations between assets translate into an efficient frontier of portfolios. A multi-asset portfolio’s expected return is given as follows:

• \( E\left( { R }_{ p } \right) =\sum _{ i=1 }^{ n }{ { w }_{ i }E\left( { R }_{ i } \right) } \hspace{0.5em} \text{where} \hspace{0.5em} { w }_{ i }= \text{weight of the asset class} \hspace{0.5em} i \hspace{0.5em} \text{in the portfolio} \)

The portfolio risk is given as follows:

• \( { \sigma }_{ p }=\sqrt { \sum _{ i=1 }^{ n }{ { w }_{ p,i } } \sum _{ j=1 }^{ n }{ { w }_{ p,j } } Cov\left( { R }_{ i },{ R }_{ j } \right) } \hspace{0.5em} \text{where} \hspace{0.5em} Cov\left( { R }_{ i },{ R }_{ j } \right) ={ \rho }_{ i,j }{ \sigma }_{ i }{ \sigma }_{ j } \)

Potential portfolios can be plotted to form an efficient frontier that represents the portfolio with minimal risk for each level of return. When return expectations for an asset class increase while volatility and correlation remain unchanged, the efficient frontier will move upward as each portfolio is able to generate higher returns for the same level of risk. The point at which the efficient frontier intersects the indifference curve with the highest utility represents the optimal portfolio for the investor.

The Actual Portfolio

The SAA is the first step toward determining the investor portfolio. Oftentimes, risk budgeting is the second step. This is the process of deciding the overall risk budget of the portfolio and dividing that risk over the sources of investment return. Apart from the exposure to systematic risk factors as specified by the SAA, the portfolio returns also depend on tactical asset allocation (TAA) and security selection.

TAA is the decision to deliberately deviate from the SAA or policy weights with the objective of adding value based on near-term return forecasts for the asset classes. Likewise, security selection is the attempt to generate higher returns than the portfolio benchmark by selecting securities with a higher expected return. Deviating from policy weights or overweighting particular securities creates additional return uncertainty, and the IPS should set limits for these activities.

Contrary to SAA, security selection is not rewarded with a long-run payoff to risk. It is a zero-sum game in which all investors compete against one another to identify a small number of mispriced securities. In total, the gross returns from all active investors tend to average out to the market return (the reward for taking on systematic risk), which implies that the active investor will match the market return. However, because of trading costs and active management fees, the average active manager will underperform the market net of costs. This does not mean there are no skillful active managers who consistently beat their benchmarks. Indeed, it does imply that all passive managers will beat the index. However, on average, this is the case.

As the portfolio changes due to the returns from various asset classes, the portfolio weights will gradually deviate from the policy weights. This process is referred to as drift, and the portfolio should be rebalanced back to policy weights. The rules that guide this process are referred to as the rebalancing policy.

Additional Portfolio Principles

Not all portfolios are constructed using a top-down framework. A top-down process requires a multitude of specialist asset managers to work for the same client within the same asset class. Each of these managers will manage risk relative to the client’s benchmark. However, because these benchmarks may be similar or overlapping, the aggregate may result in an underutilization of the risk budget. Another drawback is the potential for overtrading, which tends to create capital gains and may be tax-inefficient.

A core-satellite methodology was developed to circumvent these issues, rather than a top-down approach. A large chunk of the portfolio is invested on a passive or low active basis (the core), while a smaller portion is managed more aggressively (the satellite). The aim of the satellite portion is to generate a high active return. The return objective is not necessarily benchmark-cognisant. The core has a low turnover to capture the long-term systematic risk premium in a tax-optimal manner. A drawback of this approach is the difficulty of assigning the portfolio assets to portfolio managers who have various expected returns, risks, and correlations between those returns.

Question

Which statement best describes tactical asset allocation (TAA)?

A. TAA formulates the portfolio policy weights which provide exposure to systematic risk factors.

B. TAA allocates greater portions of the portfolio to those securities within the benchmark with higher expected returns.

C. TAA deliberately deviates from the SAA to generate additional returns on the basis of short-term asset class forecasts.

Solution

The correct answer is C.

Tactical asset allocation will tilt the portfolio to those asset classes expected to outperform in the short term.

On the other hand, strategic asset allocation is the policy portfolio designed to provide exposure to systematic risk factors generating portfolio returns that meet investment objectives.