ESG Considerations in Portfolio Planni ...
Environmental, social, and governance factors are collectively referred to by the acronym “ESG”.... Read More
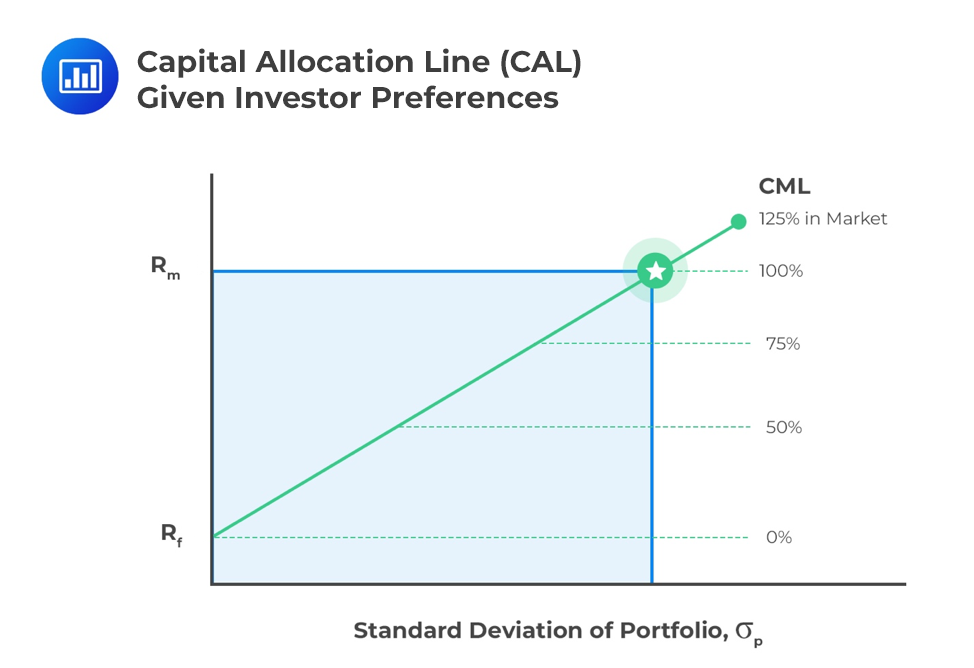
By combining a portfolio of risky assets with a risk-free asset, we can improve the return-risk characteristics of the portfolio and realize a better trade-off. This combination is called the capital allocation line (CAL). The proportion of allocation to risky assets versus allocation to risk-free assets will be dependent on the risk preferences of the investor.
Combined Portfolios
We calculate the expected return of a mixed portfolio by adding up the expected returns of its components. To assess the portfolio’s risk, we need the allocation to each component, the standard deviation of each, and the correlation between them. When the assets aren’t perfectly correlated, the portfolio’s variance will be lower than that of its individual assets.
Each investor will have their own risky portfolio, dependent on the assumptions they make on the likely performance of the underlying assets. Since every investor makes their own unique assumptions about the underlying assets, there is no one optimal risk portfolio. We need to make a simplifying assumption that investor expectations are homogenous in order to derive what would be the optimal market portfolio.
Question
If two underlying assets are negatively correlated, combining them to form a portfolio will make the portfolio risk:
A. Increase.
B. Decrease.
C. Remain constant.
Solution
The correct answer is B.
When uncorrelated assets are combined to form a portfolio, a lack of correlation will reduce the overall portfolio volatility.
Sergio Torrico
2021-07-23
Excelente para el FRM 2
Escribo esta revisión en español para los hispanohablantes, soy de Bolivia, y utilicé
AnalystPrep para dudas y consultas sobre mi preparación para el FRM nivel 2 (lo tomé una sola vez y aprobé muy bien), siempre tuve un soporte claro, directo y rápido, el material sale rápido cuando hay cambios en el temario de GARP, y los ejercicios y exámenes son muy útiles para practicar.
diana
2021-07-17
So helpful. I have been using the videos to prepare for the CFA Level II exam. The videos signpost the reading contents, explain the concepts and provide additional context for specific concepts.
The fun light-hearted analogies are also a welcome break to some very dry content.
I usually watch the videos before going into more in-depth reading and they are a good way to avoid being overwhelmed by the sheer volume of content when you look at the readings.
Kriti Dhawan
2021-07-16
A great curriculum provider. James sir explains the concept so well that rather than memorising it, you tend to intuitively understand and absorb them.
Thank you ! Grateful I saw this at the right time for my CFA prep.
nikhil kumar
2021-06-28
Very well explained and gives a great insight about topics in a very short time. Glad to have found Professor Forjan's lectures.
Marwan
2021-06-22
Great support throughout the course by the team, did not feel neglected
Benjamin anonymous
2021-05-10
I loved using AnalystPrep for FRM.
QBank is huge, videos are great.
Would recommend to a friend
Daniel Glyn
2021-03-24
I have finished my FRM1 thanks to AnalystPrep. And now using AnalystPrep for my FRM2 preparation. Professor Forjan is brilliant. He gives such good explanations and analogies. And more than anything makes learning fun. A big thank you to Analystprep and Professor Forjan. 5 stars all the way!
michael walshe
2021-03-18
Professor James' videos are excellent for understanding the underlying theories behind financial engineering / financial analysis. The AnalystPrep videos were better than any of the others that I searched through on YouTube for providing a clear explanation of some concepts, such as Portfolio theory, CAPM, and Arbitrage Pricing theory. Watching these cleared up many of the unclarities I had in my head. Highly recommended.