Capital Allocation Line (CAL) and Capi ...
We form a capital allocation line when we combine a risky asset portfolio... Read More
Given as asset systematic risk, the expected return can be computed using the capital asset pricing model. The CAPM result is usually used as a first estimate of return. In addition, it is used in capital budgeting and the determination of economic feasibility. Besides providing security expected returns, CAPM can be used for estimating the cost of capital and setting insurance premiums.
The Security Market Line (SML) is the graphical representation of the CAPM with beta reflecting systematic risk on the x-axis and expected return on the y-axis. The SML intersects the y-axis at the risk-free rate, and the slope of the line is the market risk premium, Rm – Rf.
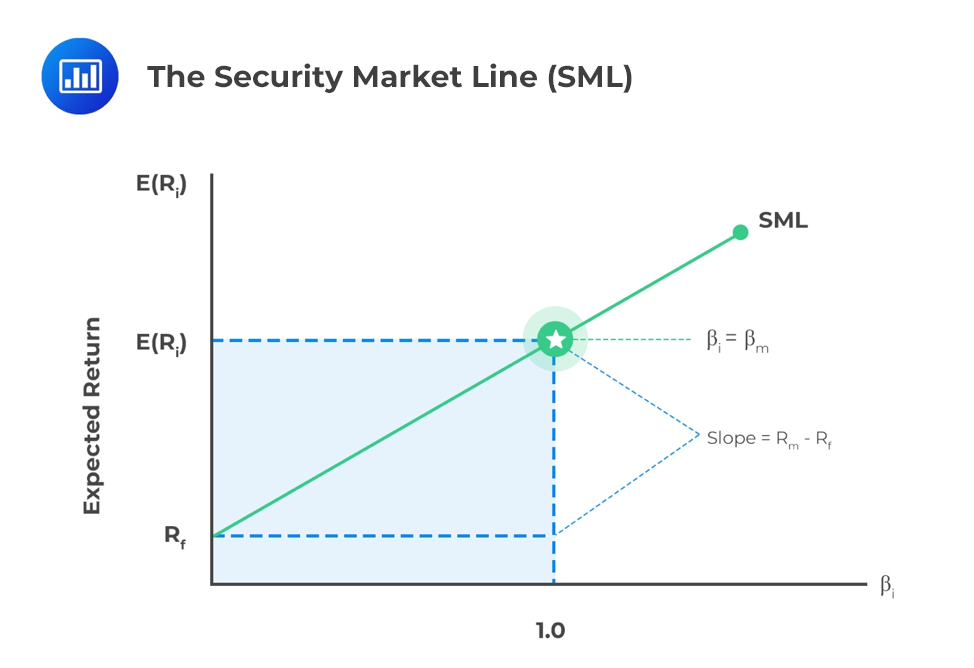
The SML is formulated as follows:
$$E(R_i) = R_f + \beta_i [E(R_m) – R_f]$$
Where \(\beta_i= \frac{\rho_{ i,m} \sigma_i } {\sigma_m}\)
With data for the risk-free rate, the market expected return, the beta of a security (or its correlation with the market), and the standard deviations of the security and the market, we can calculate the expected return using CAPM.
Question
Assume the risk-free rate is 2%, a security has a correlation of 0.8 with the market index and a standard deviation of 16%, while the standard deviation of the market is 12%. If the market expected return is 8%, what is the security’s expected return?
A. 10.56%.
B. 5.60%.
C. 8.42%.
Solution
The correct answer is C.
\(E(R_i) = R_f + \beta_i [E(R_m) – R_f]\)
Where \(\beta_i= \frac{\rho_{ i,m} \sigma_i } {\sigma_m}\)
Step 1: Find the Beta
\betai = (0.8 × 0.16) / 0.12 = 1.07
Step 2: Find the expected return
E(Ri) = 2% + 1.07 × (8% – 2%) = 8.42%
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.