Measuring and Modifying Risks

A conversation on risk would be incomplete without a mention of the ability to measure the risk. Organizations need to evaluate the cost-benefit implications of modifying their risk profiles even as they remain within the governing body risk tolerance levels.

Risk Metrics

The most basic quantitative measure or metric associated with risk is probability. Probability is a measure of the relative frequency of a particular outcome. It is incorporated into other measures of risk to provide meaningful information. Commonly used risk metrics are as follows:

Standard Deviation

Standard deviation is a measure of volatility and provides a range of potential outcomes. It has limitations as a measure for financial markets since it presumes a normal distribution of returns. This is inappropriate when we look at empirical data from the last few decades.

Like many of the financial crises before it, the 2007/2008 financial crisis brought to the fore the divergence between the normal distribution and asset return distributions. Due to the wide applicability of the normal distribution and the occurrence of normality in a broad range of phenomena, analysts have tried to fit asset returns to the normal distribution. And while this approach has had some success, it has proved unreliable and grossly inaccurate, particularly in light of the continuous and recurrent nature of financial crises.

Beta

Beta is a measure of the sensitivity of a security’s returns to the overall market portfolio. It provides an indication of systematic risk and is particularly appropriate for equity portfolios.

The Greeks

Commonly referred to as the “Greeks”, these metrics are appropriate for measuring the risk associated with derivative positions.

Delta

Delta, Δ, is a measure of the degree to which an option is exposed to changes in the price of the underlying asset. It is the ratio of the change in the price of the call option to the change in the price of the underlying asset.

For example, if we have a delta value of 0.5, it means that when the price of the underlying asset moves by a point, the price of the corresponding call option will change by half a point. If delta = 0.5, a $1 increase in the price of the underlying asset price triggers a $0.5 increase in the price of the call option.

Theta

Theta, θ, tells us how sensitive an option is to a decrease in time to expiration. It gives us the change in price of an option prompted by a one-day decrease in its time to expiration.

Options lose value as expiration approaches. Theta estimates the value lost per day if all other factors are held constant. Time value erosion is nonlinear, and this has implications on theta. As a matter of fact, the theta of in-the-money, at-the-money, and slightly out-of-the-money options generally increases as expiration nears. On the other hand, the theta of far out-of-the-money options generally decreases as expiration nears.

Gamma

Gamma, Γ, measures the rate of change in an option’s Delta per $1 change in the price of the underlying stock. It tells us how much the option’s delta should change as the price of the underlying stock or index increases or decreases. Options with the highest gamma are the most responsive to changes in the price of the underlying stock.

Vega

Vega measures the rate of change in an option’s price per 1% change in the implied volatility of the underlying stock. And while Vega is not a real Greek letter, it tells us how much an option’s price moves in response to a change in volatility of the underlying stock.

As an example, a Vega of 6 indicates that for a 1% increase in volatility, the option’s price will increase by 0.06. For a given exercise price, risk-free rate, and maturity, the Vega of a call equals the Vega of a put.

Rho

Rho measures the expected change in an option’s price per 1% change in interest rates. It tells us how much the price of an option should fall or rise in response to an increase or decrease in the risk-free rate of interest.

As interest rates increase, the value of call options will generally increase. On the other hand, as interest rates increase, the value of put options will usually decrease. Although rho is not a dominant factor in the price of an option, it takes center stage when interest rates are expected to change significantly.

Long-term options are far more sensitive to changes in interest rates than short-term options are. Furthermore, in-the-money calls and puts are more sensitive to interest rate changes compared to out-of-the-money calls and puts.

Duration

Duration is a measure of sensitivity to interest rates used for fixed-income instruments. We will see how to compute duration in the Fixed Income chapter.

Value at Risk (VaR)

VaR can be defined as the minimum amount of loss that can be incurred with a given confidence level(under normal business conditions). It can also be viewed as the worst possible loss under normal conditions over a specified period. Suppose an analyst calculates the monthly VaR as $100 million at 95% confidence level: what does this imply?

This simply means that under normal conditions, in 95% of the months, we expect the fund to make a profit or loss of no more than $100 million. Put differently, the probability of losing $100 million or more in any given month is 5%.

Limitations of VaR

• It does not describe the worst possible loss. Indeed, as seen from the example above, we would expect the $100 million loss mark to be breached 5 times out of a hundred for a 95% confidence level.
• VaR does not describe the losses in the left tail. It indicates the probability of a value occurring but stops short of describing the distribution of losses in the left tail.
• Two arbitrary parameters are used in its calculation – the confidence level and the holding period. The confidence level indicates the probability of obtaining a value greater than or equal to VaR. The holding period is the time span within which we expect the loss to be incurred, say, a week, month, day, or year. VaR increases at an increasing rate as the confidence level increases. VaR also increases with increases in the holding period.
• VaR estimates are subject to both model risk and implementation risk. Model risk arises from incorrect assumptions while implementation risk is the risk of errors from the implementation process.

Conditional Value at Risk (CVaR)

The expected shortfall (ES), also known as the conditional VaR (CVAR), is the average of losses defined by the probability. In other words, it is the expected loss given that the portfolio return already lies below the pre-specified worst-case quantile return (e.g. 5th  percentile).

Consider this: the 5% VaR for a fund is -25%. Therefore, 5% of the time, the fund earns a return that’s less than -25%. The expected shortfall gives as the expected value of all returns falling at or below the 5 percentile return. As such, ES is a larger loss than VaR. However, unlike the VaR, ES satisfies the subadditivity property.

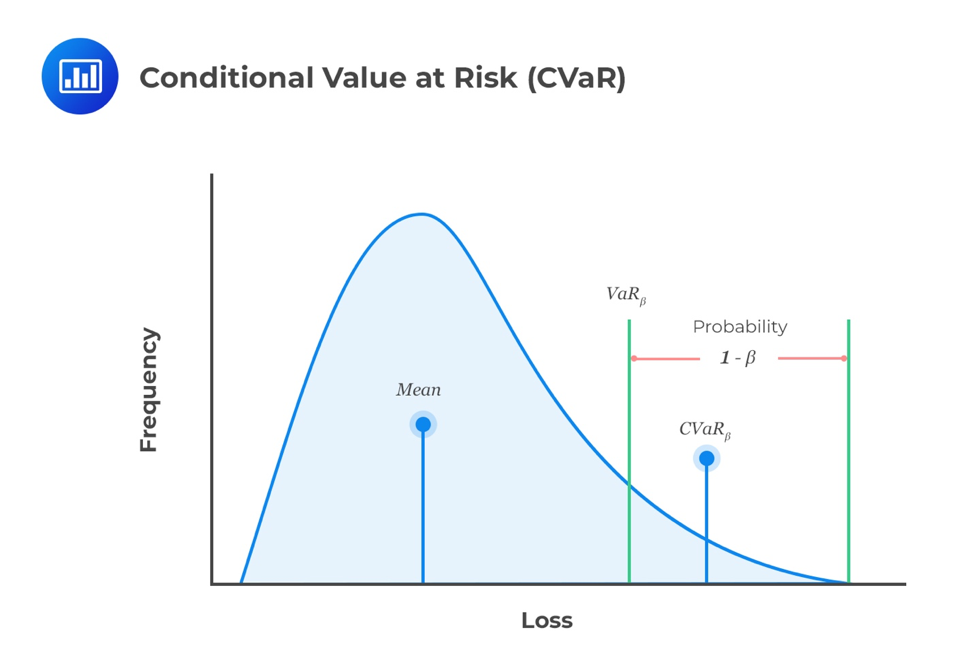
The ES is considered a better risk measure than VaR because, unlike VaR, ES gives an estimate of the magnitude of a loss for unfavorable events.

Scenario Analysis and Stress Testing

In order to complement VaR measures, scenario analysis, and stress testing are undertaken to try and understand the expected loss under different market stress conditions. One of the approaches that have been used to incorporate stress tests in VaR models involves trying to assess whether the stress test loss is part of the loss distribution developed in the VaR estimation. This way, a hypothetical/historical stress scenario can be associated with a given probability.

Credit Risk

Credit risk, which pertains to fixed-income securities, relies on a combination of credit ratings provided by credit rating agencies as well as measures of liquidity, solvency, profitability, and leverage. Credit Default Swaps (CDS) also provide information on the potential risk of default.

Operational Risk

The operational risk stems from internal functions or processes, systems, infrastructural flaws, human factors, and outside events. Operational risks are particularly hard to quantify but can be costly should they occur.

Modifying Risks

Risk modification is not necessarily about risk reduction. It may be about the deflection of risk towards the desired risk target or exposure. There are four main categories of risk modification:

Risk Prevention and Avoidance

It is difficult to completely avoid risk. The decision to avoid a specific risk altogether will be made at a board level. It is here where it will be determined that some business activities are not worth pursuing based on the risk-return tradeoff.

Risk prevention and avoidance are part of the decision on how much risk to accept and it encompasses a trade-off between the cost and the benefit.

Risk Acceptance

In many cases, it makes sense to be exposed to a particular risk. Even then, an individual or organization should do so in an efficient way. Individuals or companies may, for instance, choose to self-insure. This may mean simply bearing the risk or setting aside some provision to cover losses should they occur.

Another form of efficiently accepting risk is through the use of diversification.

Risk Transfer

Risk transfer is the process of passing risk from one party to another and may take the form of an insurance policy. The insurer charges a premium in return for insuring a specific event. The insurer pools risks by selling a large number of diversified insurance contracts with uncorrelated risks.

Risk Shifting

Risk shifting refers to changing the distribution of risk outcomes rather than passing the risk to another party. Risk shifting is often carried out through hedging by using financial market derivatives. Derivatives are either forward commitments or contingent claims.

Forward commitments are agreements that create a future-based transaction obligation between two parties at an agreed price or rate. These include forward contracts, futures contracts, and swaps.

Contingent claims arise in scenarios where both parties are mutually obligated to each other. Options grant the rights but not the obligation to transact. Consequently, the buyer of the option pays a premium at the start of the contract.

Selecting a Modification Method

Choosing the risk mitigation method to use is a critical part of the risk management process. No single option may have an advantage and a cost-benefit tradeoff that may be required. Low-cost precautions against risks with few benefits should always be the first step.

Organizations with strong cash flow may choose to self-insure as it tends to be the cheapest and most flexible option. Such an arrangement must, however, form part of the governance decision-making and risk tolerance process.

Risk transfer through the use of insurance is widely used but may not always be cost-effective. For financial risks, risk shifting through the use of derivatives is common.

Finally, the cost of the modification method must be balanced against the potential benefits while producing an overall risk profile that is consistent with the risk tolerance and objectives of the organization.

Question

Which risk metrics are often used within a fixed income portfolio?

A. Beta, delta, and standard deviation

B. Credit rating, CDS, and duration

C. VaR, vega, and loss given default

Solution

The correct answer is B.

The metrics commonly used to measure risk in fixed income portfolios are credit ratings, CDS pricing, duration as well as solvency, liquidity, profitability, and leverage.