Risk-Neutrality in Derivative Pricing

Remember that the value of an option is not affected by the real-world probabilities of the underlying price increments or decrements but rather by the expected volatilities (\(R^u\) and \(R^d\) ), which are required to price an option.

We can compute the value of a call option today by discounting its expected value at expiration at the current risk-free rate, as summarized in the equation below:

$$c_0=\frac{\pi c_1^u+(1-\pi)c_1^d}{(1+{r)}^T}$$

Similarly, the value of the put option is given by:

$$p_0=\frac{p_1^u+(1-\pi)p_1^d}{(1+{r)}^T}$$

The risk-neutral probability (denoted by \(\pi\)) is defined as the computed probability used in binomial option pricing that equates the discounted weighted sum of the expected values of the underlying to the option’s current price. It is calculated using the risk-free rate and the assumed up-and-down gross returns of the underlying, as follows:

$$\pi=\frac{(1+r)-R^d}{R^u-R^d}$$

Risk-neutral pricing is the process of determining the risk-neutral probability (which is used to calculate the present value of future cash flows) using only the expected volatilities, i.e., (\(R^u\) and \(R^d)\), and the risk-free rate.

Example: Risk-neutral Probability

A company is considering selling a one-year call option on a non-dividend paying stock whose current price is $80. The exercise price of the call option is $85, and the risk-free interest is 4%.

If the stock price is expected to go up or down by 30%, what is the selling price of the option? (Using risk-neutral pricing).

Solution

Consider the following diagram:

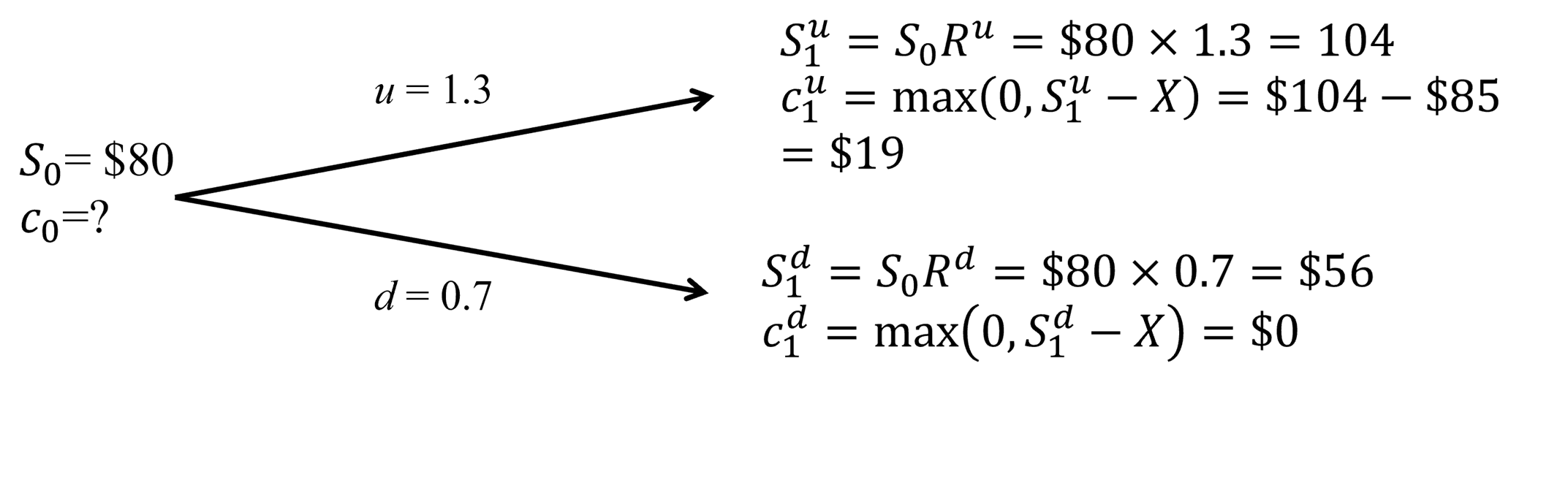
Risk neutral probability of an upward move is given by:

$$\pi=\frac{(1+r)-R^d}{R^u-R^d}=\frac{1.04-0.7}{1.3-0.7}=0.56667$$

Intuitively, the risk-neutral probability of a downward move is given by:

$$1-\pi=1-0.56667=0.43333$$

We need:

$$c_0=\frac{\left[c_1^u+\left(1-\pi\right)c_1^d\right]}{1+r}=\frac{0.56667\times19+0.43333\times0}{1.04}=$10.35$$

Question

A European call option that expires in one year has an exercise price of GBP 70. The spot price of the underlying asset is GBP 70.  Suppose that the underlying price is expected to increase or decrease by 20% within the next year, assuming a risk-free interest rate of 5%. The no-arbitrage price of a put option on the underlying asset (with similar exercise price and time to maturity) using the binomial model is closest to:

A. GBP 10.00.

B. GBP 14.00.

C. GBP 24.04.

Solution

Step 1: Determine the call option’s value at maturity.

$$\begin{align}S_1^u&=\frac{120}{100}\times70=84\\ S_1^d&=\frac{80}{100}\times70=56\\ c_1^u&=\max\ \left(0,\ S_1^u-X\right)=\max\ \left(0,\ 84-70\right)=14 \\c_1^d&=\max\ \left(0,\ S_1^d-X\right)=\max\ \left(0,\ 56-70\right)=0\end{align}$$

Step 2: Determining h (the edge ratio).

$$h=\frac{c_1^u-c_1^d}{S_1^u-S_1^d}=\frac{14-0}{84-56}=0.5$$

Step 3: Determine the portfolio value if the price of the underlying increases or decreases.

$$\begin{align}V_1^u&=\ {hS}_1^u-c_1^u=\left(0.5\times84\right)-14=28 \\V_1^d&={hS}_1^d-C_1^d=\left(0.5\times56\right)-0=28\end{align}$$

Step 4: Determining V₀.

$$V_0=\frac{V_1}{(1+{r)}^t}=\frac{28}{(1+{0.05)}^1}=26.67$$

Note: \(V_1=V_1^d=V_1^u\).

Step 5: Determining \(p_0\) and \(c_0\).

We need,

$$c_0=\frac{\left[c_1^u+\left(1-\pi\right)c_1^d\right]}{1+r}$$

where

$$\begin{align}\pi &=\frac{(1+r)-R^d}{R^u-R^d}\\ &=\frac{(1.05)-0.8}{1.2-0.8}\\ &=0.625\end{align}$$

So,

$$\begin{align}c_0&=\frac{\left[c_1^u+\left(1-\pi\right)c_1^d\right]}{1+r}\\&=\frac{\left[14+\left(1-0.625\right)0\right]}{1.05}\\&=13.33\end{align}$$

To find \(p_0\) we need to use put-call parity:

$$\begin{align}p_0&=\ c_0-S_0+X(1+{r)}^{-T}\\&=13.33-70+70(1+{0.05)}^{-1}=10.00\end{align}$$