Compare the organizational forms of bu ...
Generally, there are three major organizations in market economies, each with specific reasons,... Read More
The target capital structure of a company refers to the capital the company is striving to obtain. In other words, target capital structure describes the mix of debt, preferred stock, and common equity expected to optimize a company’s stock price. As a company raises new capital, it will focus on maintaining this target or optimal capital structure. The value-reducing impact of the present value of expected bankruptcy costs offsets the tax shield’s value-enhancing effect from debt. The trade-off can be illustrated by incorporating the potential cost of financial bankruptcy into the value of a levered firm:
$$ V_L=V_U+tD-PV\text{(Costs of financial distress)} $$
The above equation is called the static trade-off theory of capital structure.
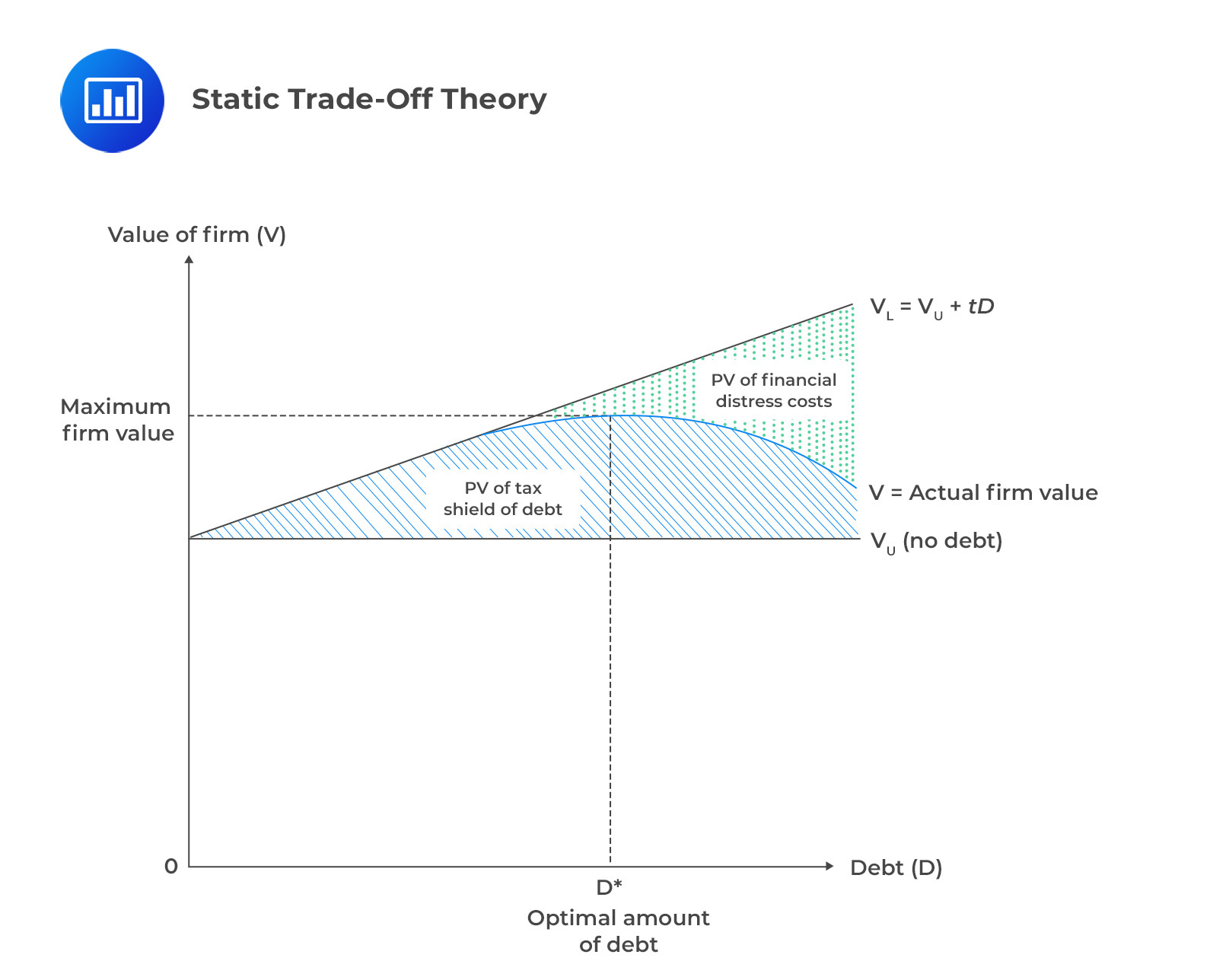
At low levels, the firm value will be higher because the tax benefit of debt will outweigh potential financial distress costs. As debt levels increase, the financial distress costs also increase and equal the tax benefit of debt. If debt levels increase further, the firm’s value will decrease as the financial distress costs exceed the tax benefit of debt. The optimal capital structure is the level at which the debt level maximizes the firm’s value and the associated equity level.
It’s important to note that earlier discussions on WACC and the weights of debt and equity were based on the market value of equity. However, when determining the target capital structure, the weights of equity and debt are calculated using their book values.
When determining target capital structure, we use book values instead of market values because:
To determine the weights to be used in the computation of the WACC of a company, a manager should ideally use the proportion of each source of capital that will be used.
For example, if a company has two sources of capital: debt and common equity:
\(w_d\), the proportion of debt:
$$ w_d =\frac{ \text{Market value of debt}}{ \left(\text{Market value of debt} \\+
\text{Market value of equity} \\+ \text{Market value of preferred stock} \right) }$$
\(w_d\), the proportion of debt:
$$ w_e =\frac{\text{Market value of equity}}{ \left(\text{Market value of debt}\\+\text{Market value of equity}\\+\text{Market value of preferred stock} \right)} $$
However, if the target capital structure is known and the company attempts to raise capital consistently with this target, then the target capital structure should be used.
An external analyst will most likely not know the target capital structure of a company and will, therefore, have to estimate it using one of the following methods:
An example will help to explain this concept further.
Example: Calculating the Capital Structure
An analyst wishes to determine the proportion of debt and equity that Company ABC would use to estimate these proportions using (i) the current capital structure of Company ABC and (ii) the average of Company ABC’s competitors’ capital structure.
The following information is given:
Company ABC’s competitors and their capital structures are:
$$ \begin{array}{c|c|c}
\text{Competitor} & \text{Market Value of Debt} & \text{Market Value of Equity} \\ \hline
X & \$20 \text{ million} & \$40 \text{ million} \\ \hline
Y & \$32 \text{ million} & \$55 \text{ million}
\end{array} $$
Solution to (i):
\(w_d\), the proportion of company ABC’s debt:
$$ w_d=\frac{\$25 \text{ million}}{\$25 \text{ million}+\$35 \text{ million}}=0.41667 $$
\(w_e\), the proportion of company ABC’s debt:
$$ w_e=\frac{\$35 \text{ million}}{\$25 \text{ million}+\$35 \text{ million}}=0.5833 $$
Solution to (ii)
\(w_d\), the arithmetic average of company ABC’s competitors’ debt:
$$ \begin{align*} w_d & =\frac{
\left(
\frac{\$20 \text{ million}}{\$20 \text{ million}+\$40 \text{ million}}\right)+\left(\frac{\$32 \text{ million}}{\$32 \text{ million}+\$55 \text{ million}}\right)}{2} \\ & =\frac{0.3333+0.36782}{2}=0.35057 \end{align*} $$
\(w_e\), the arithmetic average of company ABC’s competitors’ debt:
$$ \begin{align*} w_e & =\frac{\left(\frac{\$40 \text{ million}}{\$20 \text{ million}+\$40 \text{ million}}\right)+(\frac{\$55 \text{ million}}{\$32 \text{ million}+\$55 \text{ million}})}{2} \\ & =\frac{0.66667+0.63218}{2}=0.64943 \end{align*} $$
Although the arithmetic average is calculated in the above example, it is possible to compute the weighted average, giving greater weight to larger companies.
Managers have more information about a company’s performance and prospects—including future investment opportunities—than outsiders, resulting in asymmetric information— and unequal distribution of information.
When conflicts of interest are more likely, debt and equity capital providers demand higher returns from companies with greater information asymmetry. This is because they may suspect that new securities are overpriced. In other words, companies tend to issue equity when their shares are overvalued or new debt when their creditworthiness is about to decline.
According to the pecking order theory (Myers & Majluf, 1984), managers prioritize financing options based on the potential for revealing information. They lean first towards options that disclose the least information, like using internal funds. Conversely, they are more hesitant about public equity offerings, as these can make investors wary; if a company’s future looks bright, why would current owners dilute their ownership? Thus, when external funds are needed, managers tend to favor private debt over public ones and are most reluctant to issue equity.
Agency costs are incremental costs incurred due to the competing interests of shareholders, debtholders, and management. Items such as subsidized dinners, a corporate jet fleet, and chauffeured limousines are examples of “perquisite consumption” that executives might lawfully authorize for themselves at a cost to shareholders.
The costs arising from this conflict of interest have been called the agency costs of equity. Specific actions are taken to mitigate this risk. Such actions include requiring audited financial statements, holding an annual meeting, and using non-compete employment contracts and insurance to guarantee performance.
The free cash flow hypothesis (Jensen’s, 1986) predicts that a reduction in agency costs of equity results from an increase in the use of debt. The more financially leveraged a company is, the less room management has to take on more debt or spend money foolishly.
Question
Assume that the current market value of company XYZ’s debt and common equity are $55 million and $45 million, respectively, representing the company’s target capital structure. What are company XYZ’s target capital structure weights?
- 55% debt; 45% equity.
- 45% debt; 55% equity.
- 50% debt; 50% equity.
Solution:
The correct answer is A.
$$ w_d =\frac{\$55 \text{ million}}{\$55 \text{ million}+\$45 \text{ million}}=0.55 \\
w_e =\frac{\$45 \text{ million}}{\$55 \text{ million}+\$45 \text{ million}}=0.45
$$
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.