Defining Derivative and the Basic Feat ...
What is a Derivative? A derivative is a financial instrument that derives (obtains)... Read More
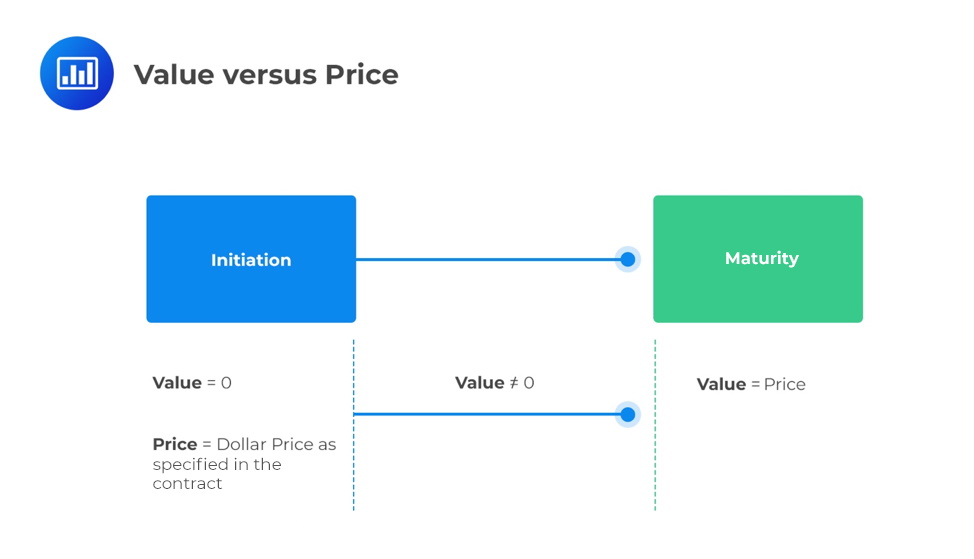
The price of a forward commitment is agreed upon at the contract’s initiation and remains fixed until the contract’s maturity. Moreover, the price is also used in determining the basis on which the underlying will be traded in the future against the spot price at maturity.
The value of a forward commitment changes over the life of the forward contract as the spot price and other factors change. For instance, consider a forward contract on an underlying that does not generate cash flows.
Define the following:
\(S_0=\) Spot price of the underlying at the initiation.
\(S_t=\) Spot price of the underlying at time t, during the contract’s life.
\(r=\) Risk-free rate of return.
\(F_0(T)=\) Forward price (satisfies the no-arbitrage conditions).
\(V_0(T)=\) Value of the forward contract at the initiation.
\(V_t(T)=\) Value of the forward contract during the life of the contract.
\(V_T(T)=\) Value of the forward contract at expiration.
Assume that there are no costs or benefits associated with the underlying. At the initiation of the forward contract, no money is exchanged, and the forward contract’s value is zero:
$$V_0(T)=0$$
The forward price that parties have agreed upon at initiation satisfies no arbitrage opportunities. As such, the forward price at initiation is the spot price of the underlying compounded at the risk-free rate over the contract’s life:
$$F_0(T)=S_0(1+R)^T$$
After its initiation, the value of the forward contract changes due to the change in the underlying’s spot price, among other factors.
As such, the mark-to-market value of the forward contract at any time, \(V_t(T)\), captures the spot price at time \(t\) and the present value of the forward price. More specifically, the value of a forward contract during the contract’s life is the spot price at time \(t\) of the underlying asset minus the present value of the forward price (long position).
And the short forward position value is calculated as follows:
$$V_T(T)=S_t-F_0(T)(1+r)^{-(T-t)}-S_t$$
Remember that this is a zero-sum game. The value of the contract to the short position is the negative value of the long position, and thus the sum of both is always zero.
Forward contract settlement depends on the difference between the forward price, \(F_0(T)\), and the spot price of the underlying at expiration, \(S_T\). Therefore, the value of the forward contract for the long position will be:
$$V_T(T)=S_T-F_0(T)$$
And the value of the forward contract for the short position will be:
$$-V_T(T)=F_0(T)-S_T$$
Assuming there are no costs or benefits associated with the underlying, study the following table.
$$\small{\begin{array}{c|c|c}\textbf{Outcome}&\textbf{Value of the Long Position}&\textbf{Value of the Short Position}\\ \hline S_t>F_0(T)(1+r)^{-(T-t)}&\text{Mark-to-market gain}&\text{Mark-to-market loss}\\ \hline S_t<F_0(T)(1+r)^{-(T-t)}&\text{Mark-to-market loss}&\text{Mark-to-market gain}\\ \hline S_t=F_0(T)(1+r)^{-(T-t)}&{\text{No mark-to-market gain/loss}}&{\text{No mark-to-market gain/loss}}\end{array}}$$
Ali Muhamud currently owns 6,000 shares at Unilever Limited, whose spot price is $134 per share. Muhamud agrees to enter a forward contract to sell 2,000 shares to a financial intermediary at $178 per share in nine months. The spot price at maturity is $197.
The contract’s value at maturity from the financial intermediary’s perspective is closest to:
Muhamud is the seller (shot position), so the financial intermediary has a long forward position. Since we’re at maturity, there is no need to take any present value. The value of the contract for the financial intermediary will simply be:
$$\begin{align*}V_T(T)&=S_T-F_0(T)\\&=\$197-\$178\\&=\$19\end{align*}$$
For a forward contract whose underlying is associated with the cost of carry, the forward price is adjusted as follows:
$$F_0(T)=[S_0-PV_0(I)+PV_0(C)](1+r)^{T}$$
Where:
\(PV_0(I)=\) Present value of income or benefits at time \(t=0\).
\(PV_0(C)=\) Present value of costs at time \(t=0\).
The forward price above satisfies the no-arbitrage condition at time \(t=0\). Moreover, the forward contract, whose underlying has associated benefits and costs, is neither a liability nor an asset to the buyer or seller. As such, the value of the contract at initiation is zero:
$$V_0(T)=0$$
During the forward contract’s life with the cost of carry, the mark-to-market (MTM) value is determined as the difference between the current spot price adjusted for the cost of carry and the present value of the forward price.
This is expressed as:
$$V_t(t)=(S_t-PV_t(I)+PV_t(C))-F_0(T)(1+r)^{-(T-T)}$$
Where:
\(PV_t(I)=\) Present value of income or benefits at any time \(t\).
\(PV_t(C)=\) Present value of costs at any time \(t\).
Since the forward price includes the cost of carry, the value of the underlying asset at maturity is calculated as the difference between the spot price at maturity, \(S_T\), and the forward price agreed upon at inception, \(F_0(T)\).
$$V_0(T)=S_T-F_0(T)$$
Nico Haas has entered a forward contract with a seller of an asset whose spot price is $62, and the net cost of carry is $5. The risk-free rate is 5% and the life of the contract is nine months. Suppose the spot price maturity remained at $62, the contract’s value at maturity is closest to:
First, let’s find the forward price:
$$\begin{align*}F_0(T)&=S_0(1-r)^{T}+PV_t(C)-PV_t(I)(1-r)^{T}\\&=(S_0+\text{Cost of carry})(1+r)^{T}\\&=(67)(1+0.05)^{\frac{9}{12}}\\&=$69.50\end{align*}$$
Therefore, the value of the contract is:
$$\begin{align*}V_0(T)&=S_T-F_0(T)\\&=\$62-\$69.50\\&=-\$7.50\end{align*}$$
The spot price, (\(S_{0,f/d}\)), and the forward price, (\(F_{0,f/d}(T)\)), are expressed in terms of price currency (foreign, f) per single unit of base currency (domestic currency, d).
The difference between the spot price and forward price depicts the difference between the risk-free foreign rate \((r_f)\) and the risk-free domestic rate \((r_d)\) as expressed below:
$$F_{0,f/d}(T)=S_{0,f/d}e^{(r_f-r_d)T}$$
At initiation, the currency with higher risk-free rates is said to trade at a forward discount, while a currency with a low risk-free rate for the forward period trades a forward premium.
At any time, \(t\) before maturity, the mark-to-market (MTM) value of the forex exchange forward is the spot price, \(S_{t,f/d}\), minus the PV of the forward price, \(F_{0,f/d} (T)\), discounted by the difference in the risk-free rates \(r_f-r_d\) over the remainder of the contract using continuous compounding, \(e^{-(r_f-r_d)(T-t)}\):
$$V_t(T)=S_{t,f/d}-F_{0,f/d} (T)e^{-(r_f-r_d)(T-t)}$$
The fluctuation between the foreign and domestic risk-free rates indicates changes in the available opportunity costs between the two currencies.
Question
Suppose Ceriotti Cosmas has 20,000 shares of VIVO, and he agrees to enter a 3-month forward contract with Lumis to sell his shares at CAD 239 per share. The risk-free rate is 3.5%, and a spot rate at \(t=0\) is CAD 225 per share. If VIVO’s spot price falls to CAD 215 per share in one month, the forward contract’s mark-to-market (MTM) value in VIVO’s perspective in one-month is closest to:
- 21.27
- 22.63
- 32.36
Solution
The correct answer is B From VIVO’s perspective: $$V_T(T)=F_0(T)(1+r)^{-(T-t)}-S_t$$Where, \(F_0(T)=CAD 239\), \(r=0.035\), \(T=0.25\), \(0.0833\), \(S_t= CAD 215\) $$\begin{align*}V_t(T)&=\text{CAD 239}(1.035)^{-(0.1670)}-215\\&=\text{CAD 22.63 MTM gain}\end{align*}$$
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.