Properties of Continuous Uniform Distribution

The continuous uniform distribution is such that the random variable \(X\) takes values between \(a\) (lower limit) and \(b\) (upper limit). In the field of statistics, \(a\) and \(b\) are known as the parameters of continuous uniform distribution. We cannot have an outcome of either less than \(a\) or greater than \(b\).

The probability density function for this type of distribution is:

$$ { f }_{ x }\left( x \right) =\frac { 1 }{ b -a } \quad \quad a< x < b $$

\(X \sim U (a,b)\) is the most commonly used shorthand notation read as “the random variable \(x\). It has a continuous uniform distribution with parameters \(α\) and \(β\).”

The total probability is spread uniformly between the two limits. Intervals of the same length have the same probability.

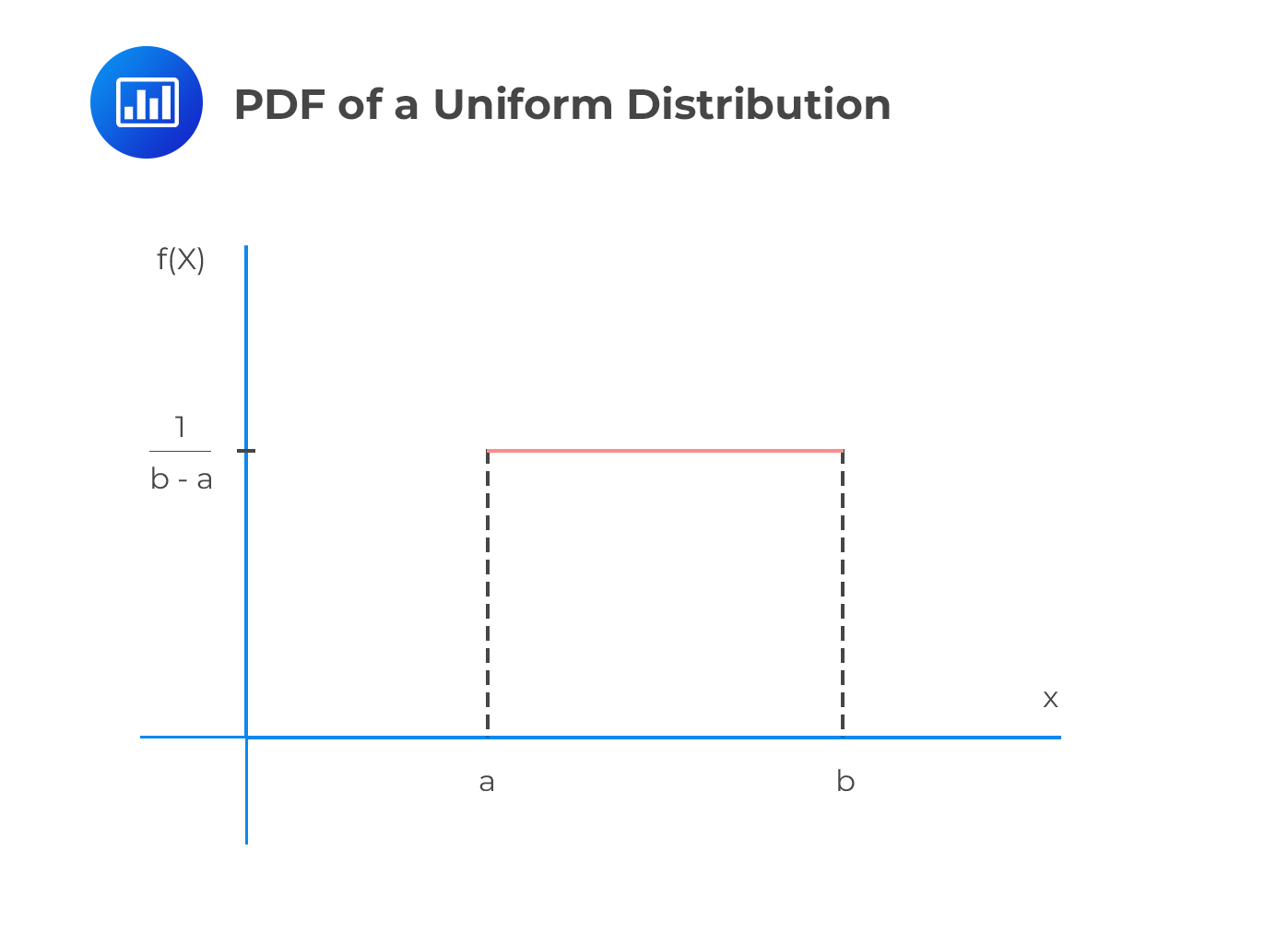
In other words, for all \(a \le x_1 < x_2 \le b\), we have

$$P(X < a) = P(X > b = 0)$$

And the probability that the random variable will have a value between \(x_1\) and \(x_2\) is given as follows:

$$P(x_1 \le X \le x_2) =\cfrac {(x_2 – x_1)}{(b – a)}$$

The mean and variance of continuous uniform distribution is given below:

$$ \text{Mean} =\cfrac {(a + b)}{2} $$

$$ \text{Variance} =\cfrac {(b – a)^2}{12} $$

Example: Probability Density Function

You have been given that \(Y \sim U(100,300)\).

Calculate \(P(Y > 174)\) and \(P(100 < Y < 226\).

Solution

The probability density function is given by:

$$ f_x(x) =\cfrac {1}{(300 – 100)} =\cfrac {1}{200} $$

Therefore, each “unit interval” has a probability of \(\frac {1}{200}\).

This means that \(P(Y > 174) =\cfrac {(300 – 174)}{200} = \cfrac {126}{200} = 0.63\).

Similarly, \(P(100 < Y < 226) = 0.63\) because the interval has the same length as above (126) hence the same probability.

Cumulative Distribution Function of a Continuous Uniform Distribution

Remember that a cumulative distribution function, \(F(x)\), gives the probability that the random variable \(X\) is less than or equal to \(x\), for every \(x\) value. It is usually expressed as:

$$F(x)=P(X\leq x)$$

The cumulative distribution function of the continuous uniform distribution increases linearly from \(α\) to \(β\).

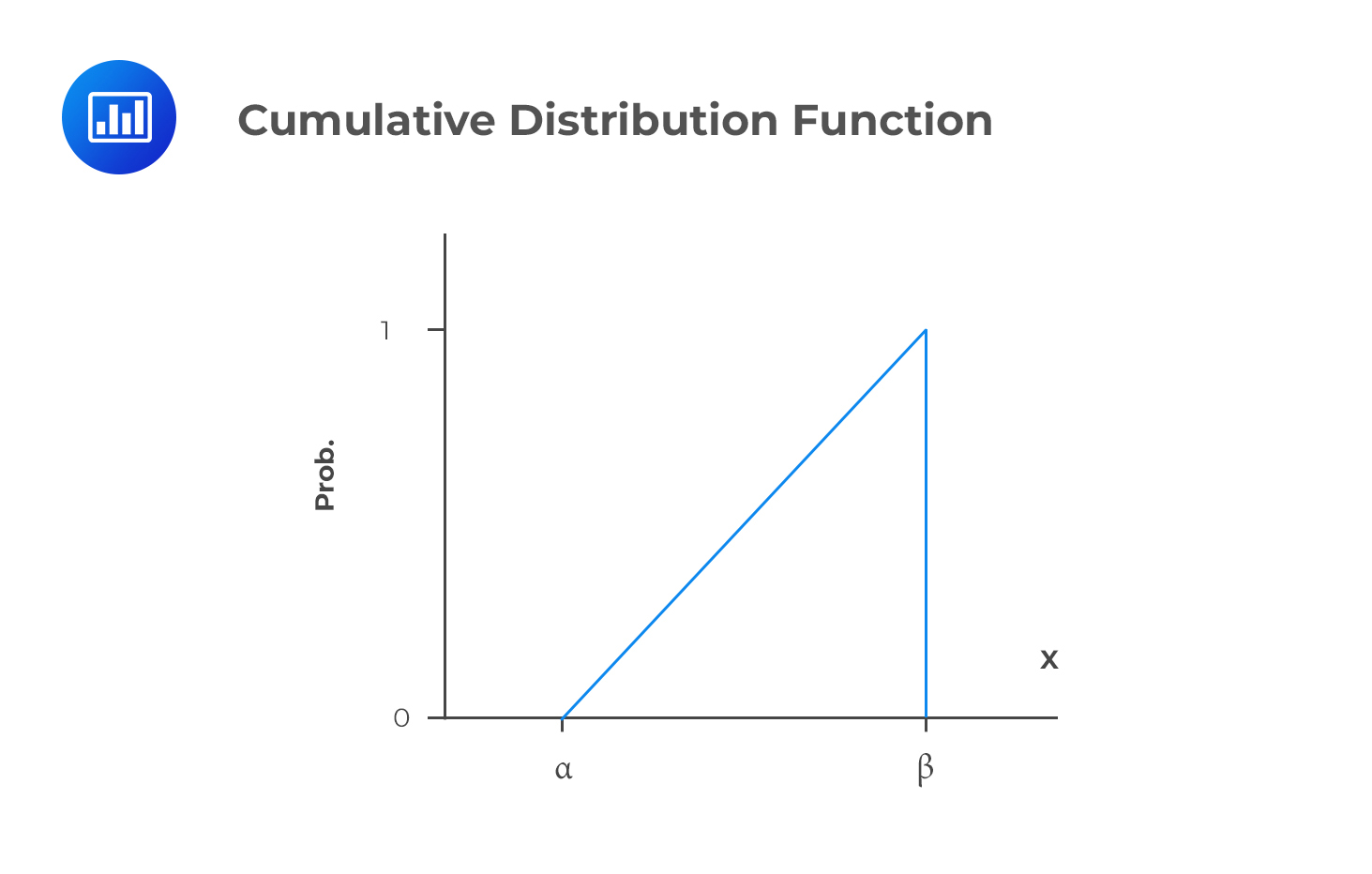
The CDF is linear over the variable’s range, and it is given by:

$$
F(x)=P(X\leq x)=\frac{x-a}{b-a}
$$

Question

A random variable \(X\) is uniformly distributed between 32 and 42. What is the probability that \(X\) will be between 32 and 40?

1. 8%.
2. 10%.
3. 80%.

Solution

The correct answer is C.

First, you should determine the pdf:

$$ \begin{align*} f_x(x) & =\cfrac {1}{(42 – 32)} \\ &=\cfrac {1}{10} \\ \end{align*} $$

Therefore,

$$ P(32 < Y < 40) =\cfrac {(40 – 32)}{10} = 0.8 \text{ or } 80\% $$