Demystifying Forward Rate Agreements (Calculations for CFA® and FRM® Exams)

A forward rate agreement (FRA) is a cash-settled over-the-counter (OTC) contract between two counterparties, where the buyer is borrowing (and the seller is lending) a notional sum at a fixed interest rate (the FRA rate) and for a specified period starting at an agreed date in the future.

The purpose of FRA is to lock in borrowing or a lending rate for some time in the future. Typically, it involves two parties exchanging a fixed interest rate for a floating rate.

An FRA involves Two Counterparties:

• The borrower: The long pays a fixed rate and receives floating rates. Think of “buying money.” If LIBOR rises, the long will gain.
• The lender: The short pays a floating rate and receives a fixed rate. Think of “selling money.” If LIBOR falls, the short will gain.

The FRA buyer enters into the contract to protect itself from a future increase in interest rates; the seller of the FRA wants to protect itself from a future decline in interest rates.

FRM Part 1 and Part 2 Complete Online Course

Naming Convention (FRM Exam)

FRAs are denoted in the form of “X × Y,” where X and Y are months. So, a 1 × 4 FRA is called “1 by 4”.

Implying that:

A 1 × 4 FRA expires in 30 days (one month), and the theoretical loan is for a time period of the difference between 1 and 4 (three months = 90 days). That is, a three-month Libor determines the FRA’s payoff, but the FRA expires in one month.

Example 1: Understanding FRAs 

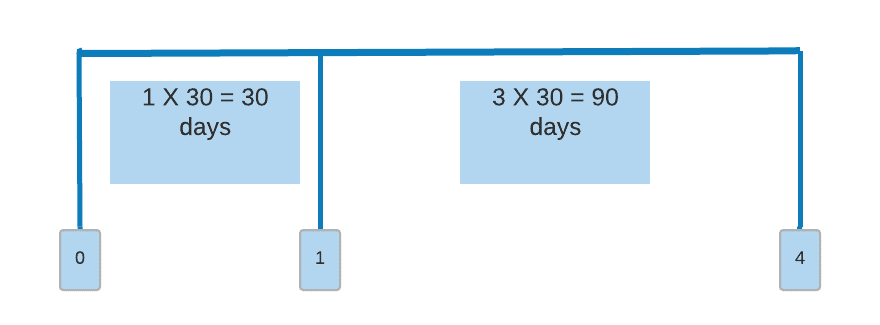
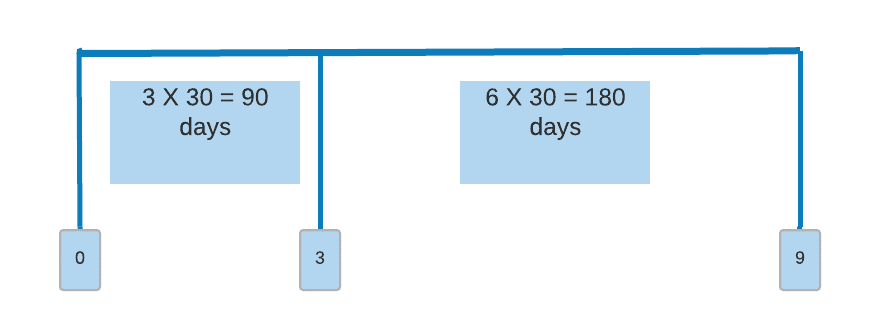
A 3 × 9 FRA refers to:

1. A 90-day LIBOR loan starting 270 days from now.
2. 270-day LIBOR loan starting 90 days from now.
3. 180-day LIBOR loan starting 90 days from now.
4. 270-day LIBOR loan starting 180 days from now.

Solution

The correct answer is C.

3-by-9 means a 180-day LIBOR loan starting 90 days from now.

FRA vs. Forwards

The forward rate specified in the FRA is compared with the current LIBOR rate, where:

• • If the current LIBOR is greater than the FRA rate, the long can effectively borrow at a below-market rate. The long receives a payment based on the difference between the two rates.
  • However, if the current LIBOR was lower than the FRA rate, then long makes a payment to the short. The payment ends up compensating for any change in interest rates since the contract date

Illustration

Example 2: FRA Valuation

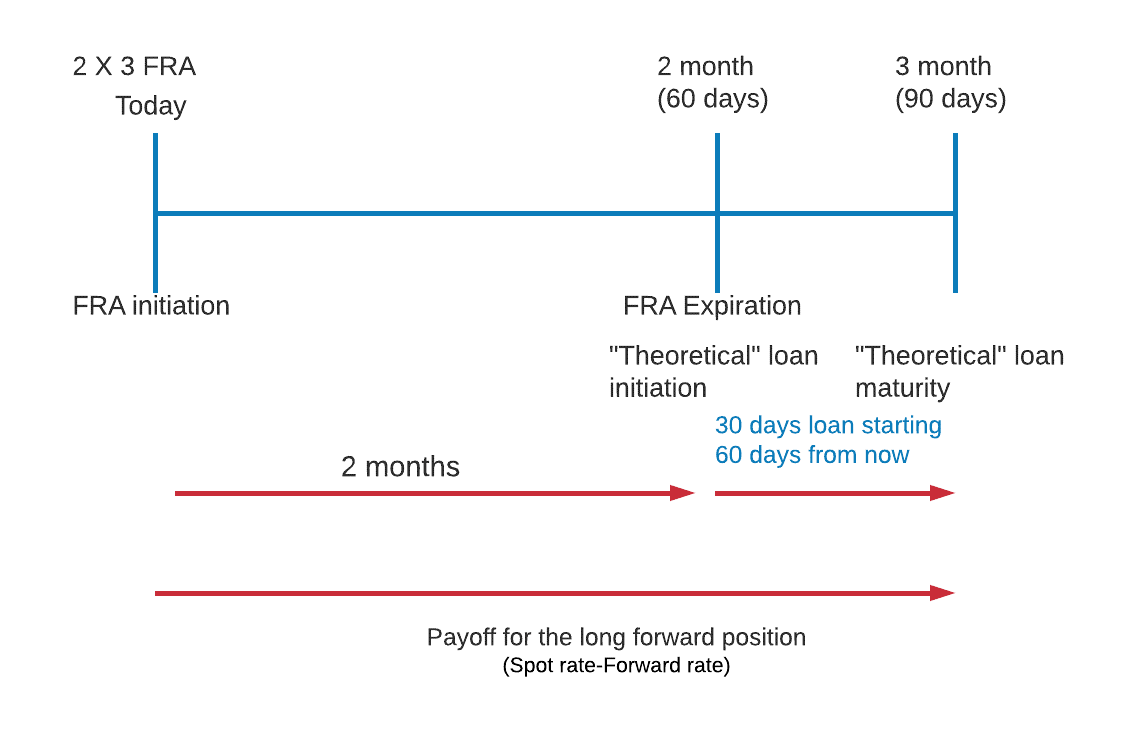
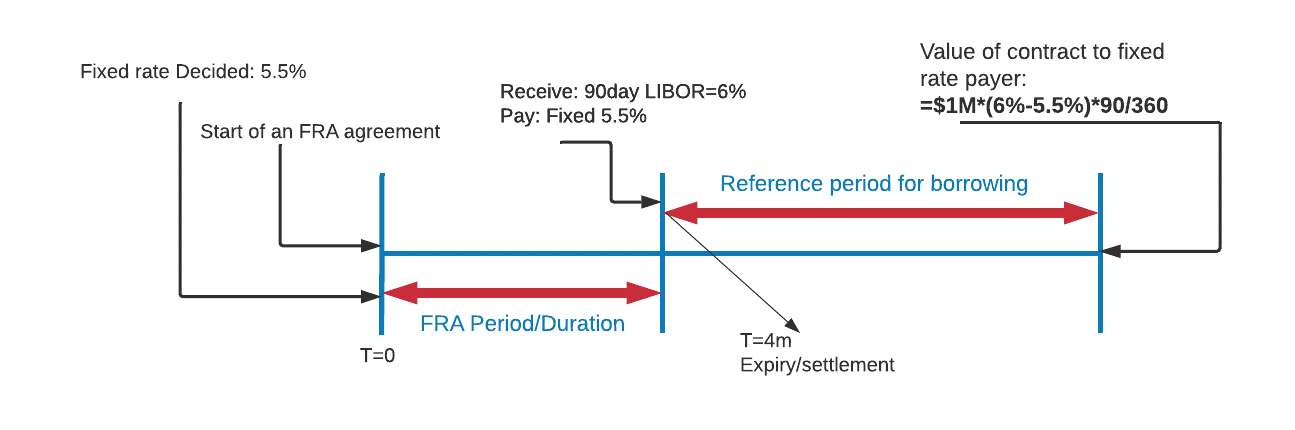
Suppose we have a 1 x 4 FRA with a notional principal of $1 million. At contract expiration, the 90-day LIBOR at settlement is 6% and the contract rate is 5.5%.

The value of the FRA at maturity is closest to:

Solution

$$ \begin{aligned} &\begin{array}{c} \text{Payment} \\ \text{to the Long} \end{array} = \text{Notional principal} \times \frac{(\text{Rate at settlement} – \text{FRA rate}) \times \frac{\text{Days}}{360}}{1 + \text{Rate at settlement} \times \frac{\text{Days}}{360}} \end{aligned} $$

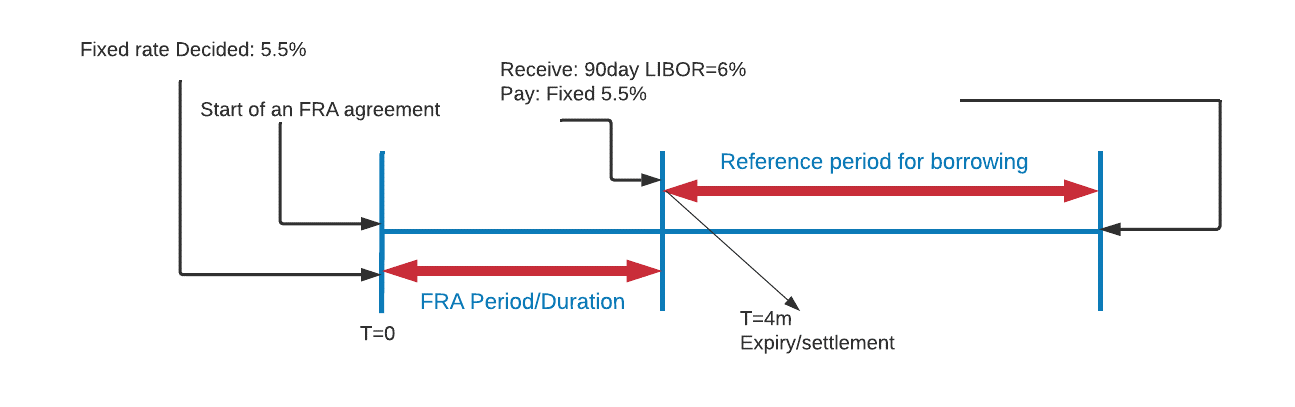
Since the settlement rate is higher (6%) than the contract rate (5.5%), the buyer will be receiving money from the seller. The payment to the long at settlement are as follow:

Interest saving:

$$=(6\%-5.5\%)\times\frac{90}{360}\times1\text{m}=1,250$$

Discounted back 90 days @ 6%:

$$=\frac{1,250}{[1+\frac{90}{360}\times6\%]}={1,231.53}$$

$$ \begin{array}{l|c|c} \textbf{Feature} & \textbf{Forward Rate Agreement (FRA)} & \textbf{Forward Contract} \\ \hline \text{Purpose} & \text{Interest Rate Hedging} & \text{Price Hedging} \\ \hline \text{Settlement} & \text{Cash-Settled} & \text{Physical Delivery} \\ \hline \text{Common Use} & \text{Loans & Borrowing Costs} & \text{Commodities, FX} \\ \hline \text{Tested In} & \text{CFA & FRM Exams} & \text{CFA & FRM Exams} \\ \end{array} $$  

View Full CFA Course