Private Clients versus Institutional C ...
Private clients typically refer to individuals and families looking to invest their wealth.... Read More
As discussed, mean-variance analysis can help investors and advisors begin to zero in on an asset allocation while considering asset correlations, total return, and total risk. Effectively use of MVO will result in a specific set of output for current asset allocations, e.g.:
One of the main criticisms of this result is that it is a single-period output. In real-world applications, investors want to know how their portfolios will behave over time, given various allocations, interest rates, tax rates, etc. In other words, building, properly managing, and utilizing wealth is an ongoing, life-long process—Monte Carlo simulation steps in at this point to bridge the gap.
Monte Carlo Simulation is essentially a random-number generator. The user will define realistic limits on variables such as expected asset class returns, volatility, and correlation. The generator will go through thousands of iterations, creating a random yet realistic set of outcomes for a portfolio over the specified time horizon.
This randomly generated path allows the analyst to view realistic outcomes of a plan, as pictured below, to decide whether the chosen asset allocation results in acceptable portfolio outcomes as predicted by MCS.
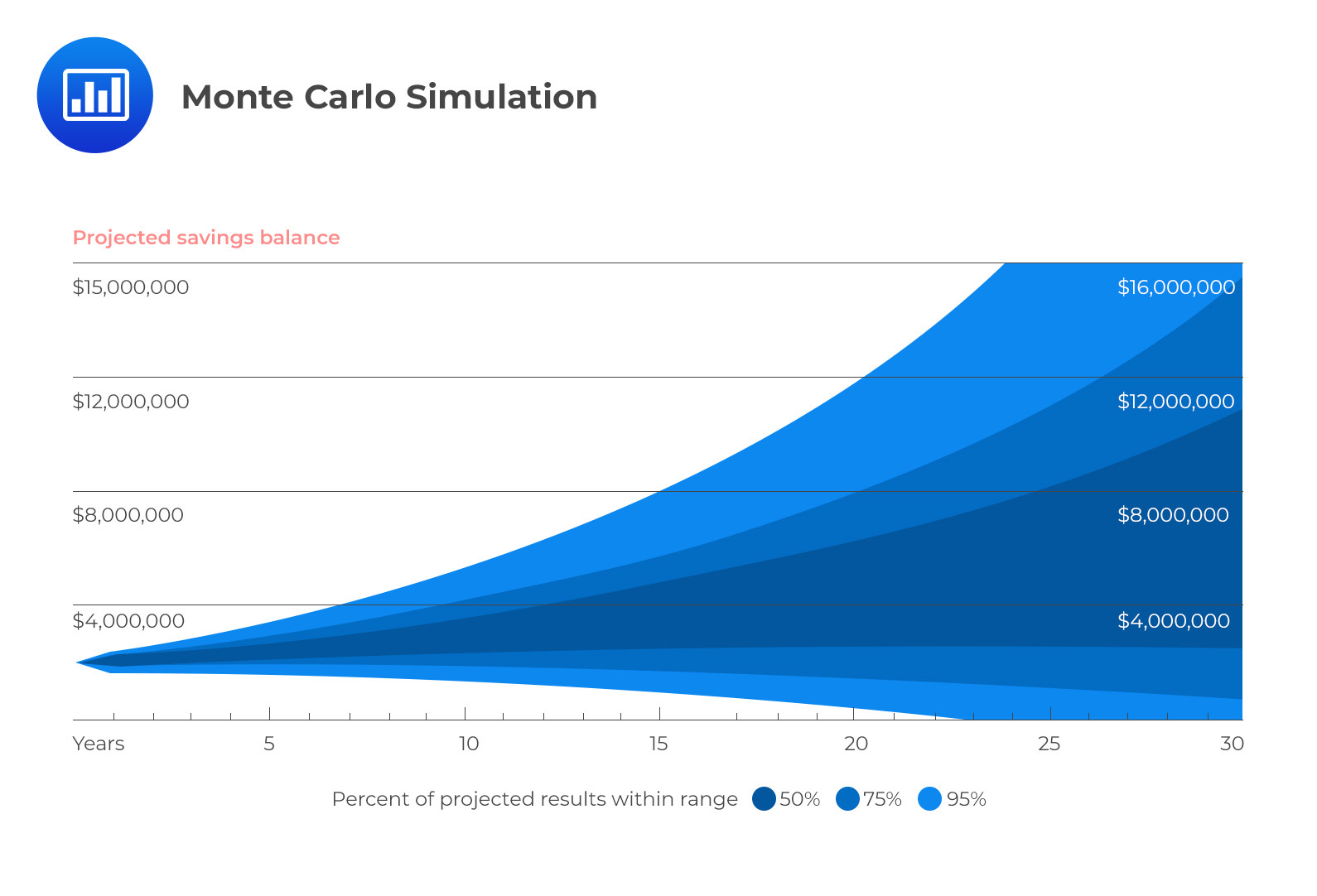 Monte Carlo simulations enable investment advisers to deal with practical issues that are difficult or impossible to analyze analytically. It may be appropriate for a taxable investor to rebalance their assets into a strategic asset allocation. It is easy to calculate the tax impact during a single period. MVO assumes that rebalancing is irrelevant in single-period settings.
Monte Carlo simulations enable investment advisers to deal with practical issues that are difficult or impossible to analyze analytically. It may be appropriate for a taxable investor to rebalance their assets into a strategic asset allocation. It is easy to calculate the tax impact during a single period. MVO assumes that rebalancing is irrelevant in single-period settings.
In most multi-period investment problems, however, capital gains and losses will be realized when the portfolio is rebalanced. Tax payments (and transaction costs) will vary depending on a specific rebalancing rule. Mathematically formulating the multi-period problem would be difficult. A Monte Carlo simulation would more efficiently incorporate the interaction between rebalancing and taxes.
Choosing among asset allocations can be determined by an investor’s wealth at the end of their time horizon. Risk and return interact to determine future wealth. An asset allocation needs to be evaluated using Monte Carlo simulation based on whether or not cash flows are coming into or going out of the portfolio. When an asset allocation does not generate cash flows, the sequence of returns is irrelevant; ending wealth is path-independent (unaffected by the trajectory of returns). Simulated returns are also independent and identically distributed if cash flows are simulated. The analysis could find terminal wealth expected and percentiles. Typically, terminal wealth depends on the sequence of returns (the interaction between cash flows and returns) since investors save/deposit money and spend money from their portfolios.
Question
Monte Carlo Simulation can most likely remedy which of the following shortcomings of mean-variance analysis?
- Sources of risk may not be diversified.
- Allocations are not ideal for valuing liabilities.
- Single-period framework.
Solution
The correct answer is C:
MVO is a single-period framework that does not consider trading/rebalancing costs and taxes. In other words, MVO is a recommendation for an asset allocation, a single snapshot in time. Investors are commonly more worried about how the portfolio will likely behave over its lifetime and what kind of outcomes are realistic for similar portfolios. This is where the Monte-Carlo simulation shines.
A is incorrect. Diversification of risk is a fundamental concept in portfolio theory and is addressed by mean-variance analysis. Mean-variance analysis seeks to construct portfolios with the highest expected return for a given level of risk, where risk is measured by the variance (or standard deviation) of the portfolio’s returns. Diversification is achieved by combining assets to reduce the overall portfolio risk.
B is incorrect. Mean-variance analysis is used to construct efficient portfolios, not value liabilities. Valuing liabilities involves estimating the present value of future cash flows, which is a separate issue from constructing an efficient portfolio.
Asset Allocation: Learning Module 4: Principles of Asset Allocation; Los 4(e) Discuss the use of Monte Carlo simulation and scenario analysis to evaluate the robustness of an asset allocation
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.