Standard VI(C) – Referral Fees
Members and Candidates must disclose any remuneration, consideration, or advantages received from or... Read More
Until this point in the curriculum, the strategies we discussed involved combinations of options and stock positions. However, the following strategies can be created using just two option positions. While spreads and straddles are often standalone strategies without the need for the underlying stock, a collar strategy protects gains on a long stock position. Nevertheless, it can also be used as a bearish play where a put is purchased and a call sold to help finance the put purchase. It’s equally noteworthy that the truth of a position can be determined by analyzing the Greeks. For example, a position’s bullish or bearish nature can be determined by examining the delta value, with a positive delta indicating a bullish position and a negative delta indicating a bearish position. Additionally, a position with negative theta will experience a loss over time if there is no underlying movement, as it reflects the effect of time decay.
A bull spread strategy involves buying a call option with a lower strike price while simultaneously selling a call option with a higher strike price. This position is called a bull spread because it aims to profit from upward price movements in the underlying asset. The bull call spread formula is simply the difference in value between two call options, with the sold call option indicated by a negative sign to represent its inverse relationship to price.
Formula:
Value at expiration
$$ \text{Value of bull call spread } (V_T) = \text{Max}(0,(S_T –K_1)) – \text{Max}(0,(S_T– K_2)) $$
Where:
\(K_1\) =Strike price of the purchased call.
\(K_2\)= Strike price of the written call.
To calculate the total profit from a bull call spread, we need to consider the value of the spread at expiration. It’s important to note that establishing a bull call spread involves an initial cash outlay. The price of the lower strike call bought should be higher than the strike price of the short call above it. If the spread’s value at expiration exceeds the initial investment, the position is profitable.
$$ \text{Breakeven} = \text{Strike price of long call} +\text{Net outlay of cash} $$
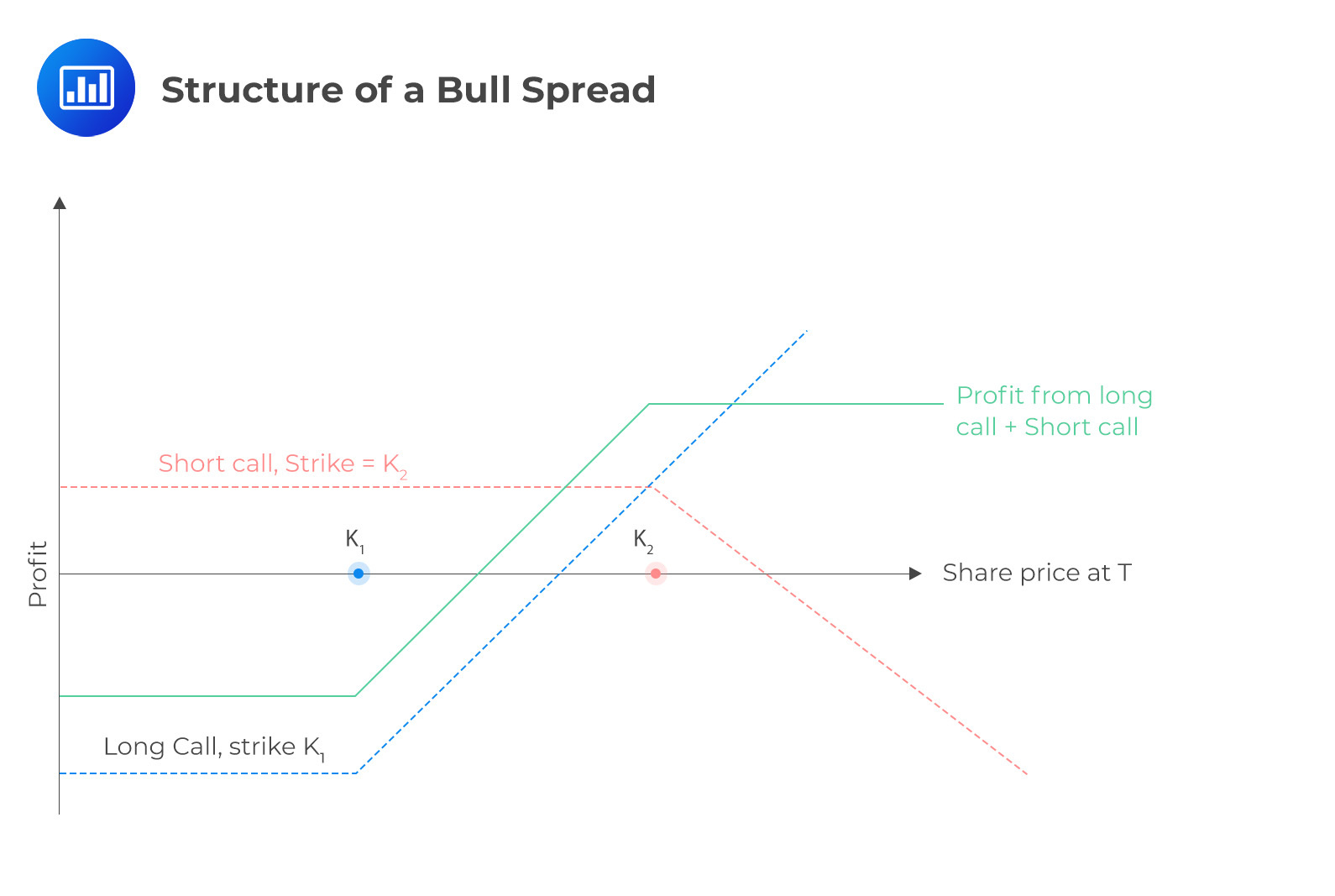
$$ \begin{array}{c|c|c|c} {\text{Stock price} \\ \text{range}} & {\text{Payoff from} \\ \text{long call option} } & {\text{Payoff from} \\ \text{short call option}} & \textbf{Total payoff} \\ \hline S_T \le K_1 & 0 & 0 & 0 \\ \hline K_1 \lt S_T \lt K_2 & S_T-K_1 & 0 & S_T-K_1 \\ \hline S_T\ge K_2 & S_T-K_1 & -(S_T-K_2) & K_2-K_1 \end{array} $$
In Summary:
Profit
$$ \text{Profit}=V_T-c_1+c_2 $$
Maximum profit
Difference between the strikes and the net premium paid.
$$ \text{Maximum profit}= K_2-K_1-c_1+c_2 $$
Maximum loss
Net premium paid.
$$ \text{Maximum loss}= c_1-c_2 $$
Breakeven
Sum of the lower strike and the net premium paid.
$$ \text{Breakeven}= K_1+ c_1-c_2. $$
Like a bull spread, a bear spread derives its name from its ability to generate profits when the underlying stock price decreases. Like a bull spread, a bear spread can be constructed using call or put options. In the following example, we will use put options to illustrate the formation of a bear spread, as candidates generally understand this approach more readily.
The structure of a bear spread is given as illustrated below:
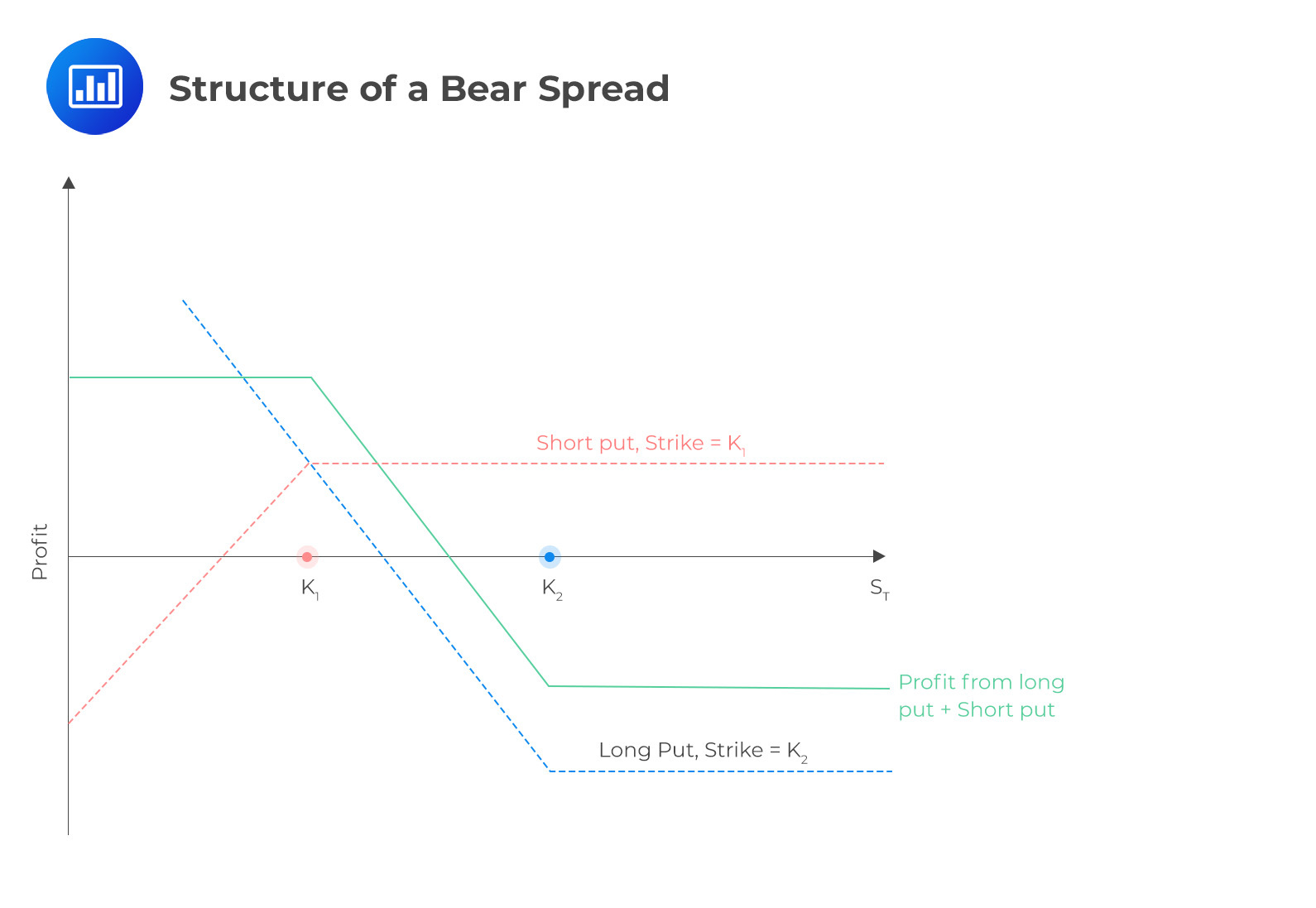
$$ \begin{array}{c|c|c|c} {\text{Stock price} \\ \text{range}} & {\text{Payoff from long} \\ \text{put option}} & {\text{Payoff from short} \\ \text{put option}} & \text{Total payoff} \\ \hline S_T\le K_1 & K_2-S_T & -(K_1-S_T) & K_2-K_1 \\ \hline K_1\lt S_T \lt K_2 & K_2-S_T & 0 & K_2-S_T \\ \hline S_T\ge K_2 & 0 & 0 & 0 \end{array} $$
$$ \text{Value of bear put spread } (v_T ) =\text{Max}(0,(K_2 – S_T)) – \text{Max}(0,(K_1 – S_T)) $$
Where:
\(K_1\) = Strike price of the sold put.
\(K_2\) = Strike price of the long put.
Remember to adjust the formula for the value at the expiration of the spread by subtracting the net premium paid to calculate the profit. In a bear put spread, a net outlay of funds needs to be considered, as the cost of purchasing the higher strike put is typically higher than the amount gained from selling the lower strike put.
Profit
It is calculated by subtracting the initial cost from the payoff.
$$ \text{Total profit} = \text{Profit from long put} + \text{profit from short put.} $$
The initial value of the bear put spread \(= p_2-p_1\).
$$ \text{Profit} = V_T-p_2+p_2 $$
Maximum profit
Maximum profit occurs when both puts are in the money at the expiry date, I.e., \(S_T\le K_1\). The short put is exercised, and the investor will buy an asset at \(K_1\) and the asset is then sold at \(K_2\) when long put is exercised.
$$ \text{Maximum Profit}=K_2 –K_1 –p_2 +p_1 $$
Maximum loss
It occurs when both puts are out of money at the expiry date, I.e.,\(S_T \gt K_2\)
$$ \text{Maximum loss} = p_2-p_1 $$
Breakeven
$$ \text{Breakeven} = \text{Strike price of long put} – \text{A net outlay of cash} $$
$$ \text{Breakeven} = K_2- p_2+p_1 $$
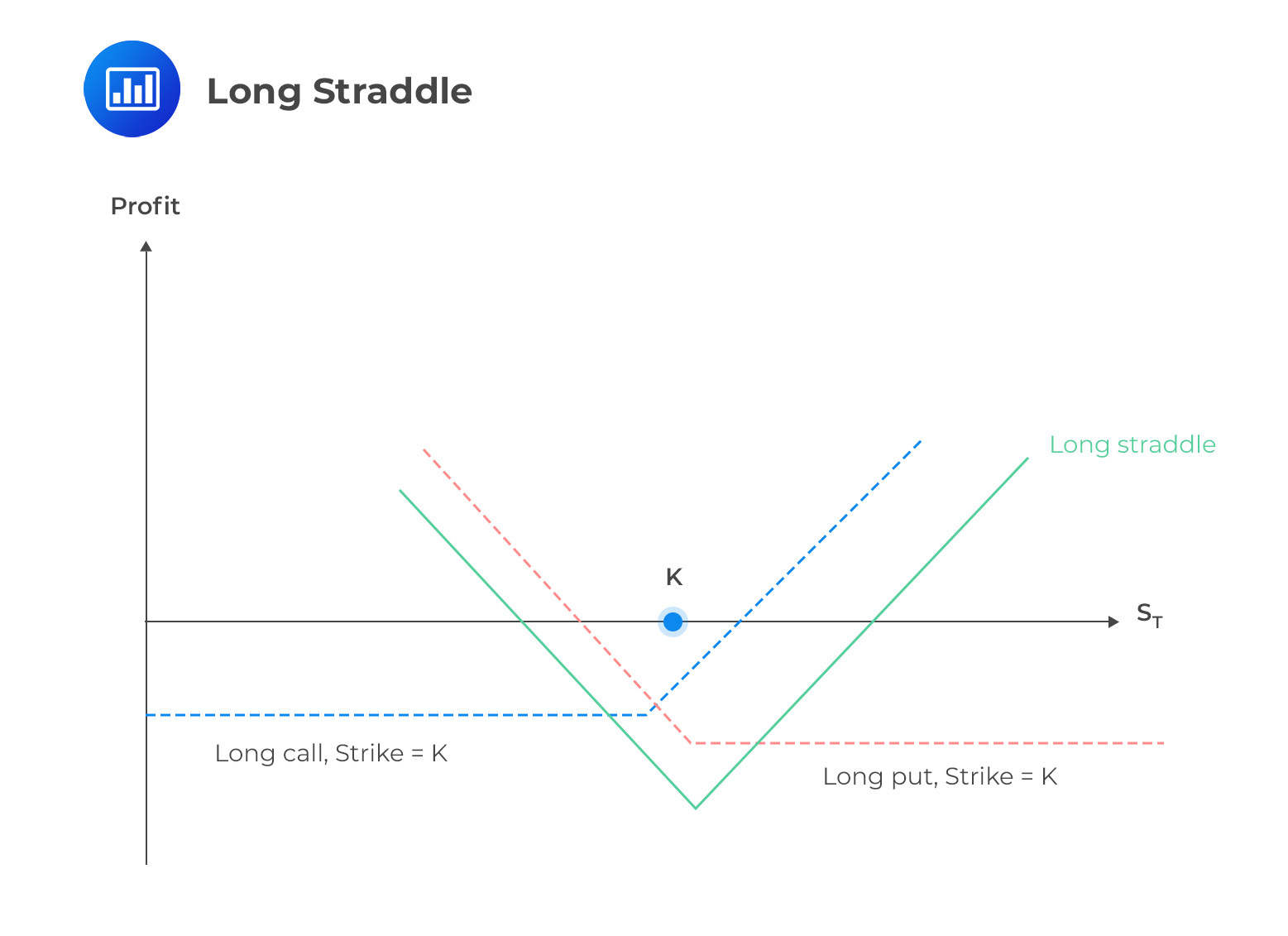
The strategies we have discussed so far have primarily focused on predicting the direction of the underlying stock’s price movement. However, the straddle introduces a different approach that can be profitable regardless of whether the stock moves up or down. Straddles involve buying both a put and a call option with the same strike price and expiration date. By widening the strike prices, a straddle can transform into a strangle. At the same time, different expiration dates can result in various calendar spreads, which we will discuss later. For a straddle to be profitable, the underlying stock must experience a significant enough movement to offset the premium paid to establish the position. This strategy tends to work best in times of high or increasing volatility.
$$ \text{Value of straddle} = \text{Value of call} + \text{Value of put} $$
In this case, the investor buys both the put and the call options with the expectation that either or both will increase in value. Both options can rise in volatility, but usually, the stock undergoes a breakout in one direction. This leads to a rapid rise in the value of one option while the other option declines toward zero.
$$ \text{Breakeven of straddle} = \text{Strike} \pm \text{premium paid} $$
The \(\pm\) indicates two breakeven points. They result from a significant move in either the underlying price’s direction or a large volatility increase. This can cause both positions to increase in value simultaneously.
An investor is interested in a tech giant, AMSN, and expects a significant price movement in one month following the company’s new product launch. The investor looks at the options prices for the stock and finds the following:
AMSN Shares trading at: 3,172.69
$$ \begin{array}{c|c|c} \textbf{Calls} & \textbf{Strike} & \textbf{Put} \\ \hline 96.30 & 3,160 & 82.35 \\ \hline 93.80 & 3,165 & 84.90 \\ \hline 91.35 & 3,170 & 87.30 \\ \hline 88.95 & 3,175 & 89.85 \\ \hline 86.40 & 3,180 & 92.35 \end{array} $$
The investor purchases a straddle at the 3,175 strike, closest to the current stock price. The straddle is bought at a combined cost of $178.80, considering the prices of both the call and the put options. Although options are typically traded in round lots of 100 shares, we’ll disregard that convention for simplicity. For the investor to start making a profit, the price of ASMN shares must move more than $178.80 per share in either direction by the options’ expiration date.
$$ \text{Breakeven upside} = \$3,175 + \$178.80 = \$3,353.80 $$
$$ \text{Breakeven downside} = \$3,175 – \$178.80 = \$2,996.20 $$
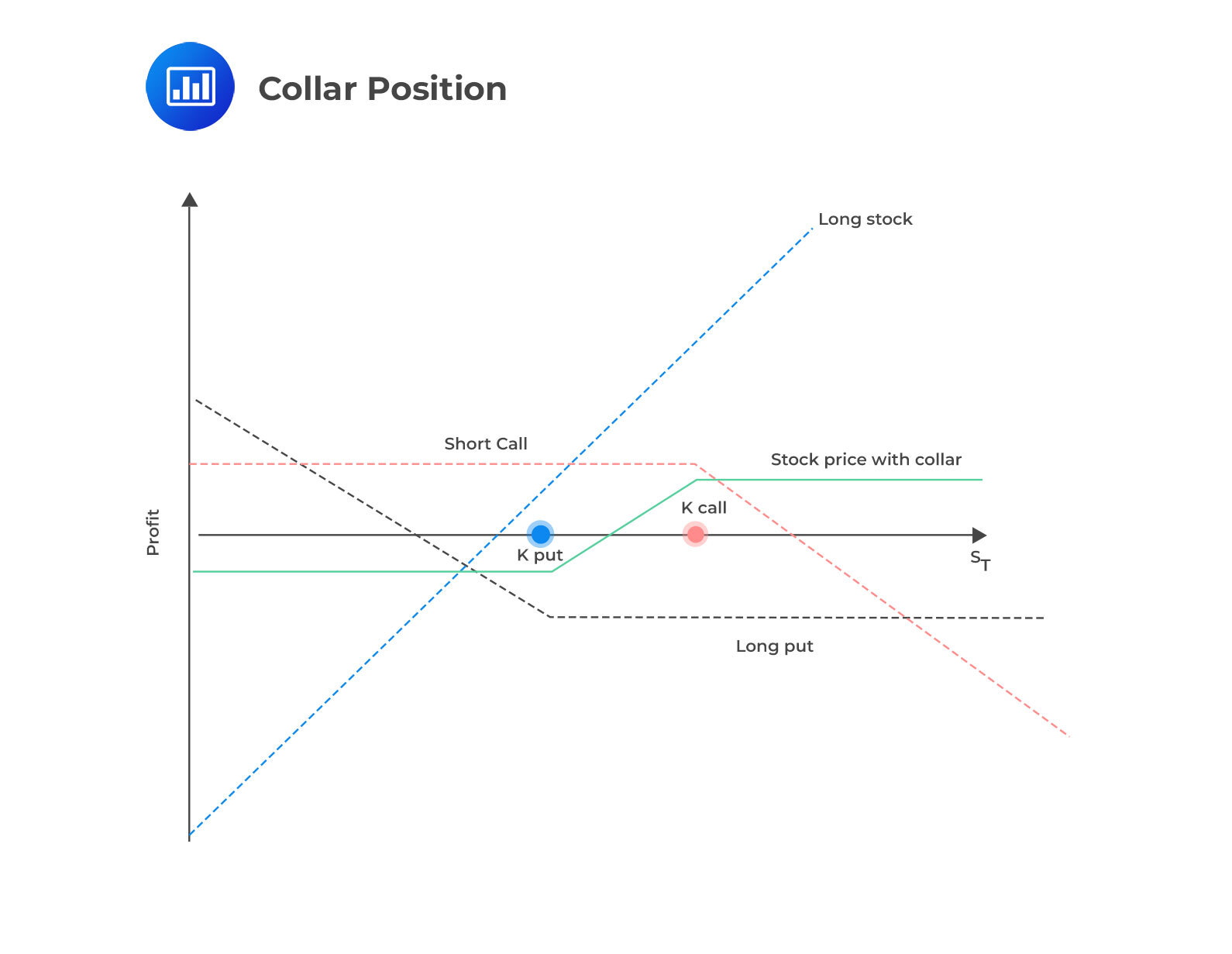
A collar strategy builds upon the concept of a married put. It involves purchasing a protective put while partially financing the cost by selling an out-of-the-money call option. Collars can be set up in various ways, but a common approach is the zero-cost collar, where the premium received from selling the call offsets the cost of buying the put.
Alternatively, a collar can be viewed as combining a covered call with a protective put. The benefit of using a collar is that it limits the potential outcomes of the strategy. The stock’s upside is capped at the short call’s strike price, while the long put protects the downside. This helps reduce volatility and lock in gains for the investor.
Formulas
The value of the collar position is equal to the sum of all its parts:
$$ \text{Value of Collar}(V_T)= S_T+ \text{Max}(0,(K_\text{Put} – S_T )- \text{Max}(0,(S_T – K_\text{Call} ) $$
Where;
$$ K_\text{call} \gt K_\text{put} $$
To calculate the net profit of a collar position, consider the value of the collar and the stock. Remember to account for any premiums involved. In a zero-cost collar, there is no premium impact on profit. If a premium payment is required (put cost exceeds call offset), subtract it from the profit. If the collar generates income, add it to the profit calculation.
Question
An investor anticipates upcoming volatility in the Swiss Equity Markets (“SMI”) due to an upcoming vote on leaving the local union. To take advantage of this situation, the investor purchases two options on the SMI ETF with the same strike price and expiration. This strategy is most likely known as?
- Straddle.
- Bear put spread.
- Collaring.
Solution
The correct answer is A.
A straddle is a strategy where an investor purchases both a call and a put option at the same strike price and with the same expiration. It is employed when there is uncertainty about the direction of price movement but an expectation that a significant event will occur.
B is incorrect. Bear put spread involves buying and selling a put at a lower strike. No call is involved.
C is incorrect. A collar is similar to a straddle in that it involves the purchase of a put option. However, instead of buying a call option, a further out-of-the-money call option is sold to create a collar position.
Derivatives and Risk Management: Learning Module 1: Options Strategies; Los 1(f) Discuss the investment objective(s), structure, payoffs, risk(s), value at expiration, profit, maximum profit, maximum loss, and the breakeven underlying price at expiration of the following option strategies: bull spread, bear spread, straddle, and collar
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.