Protective Put position

Introduction to and Objectives of the Protective Put

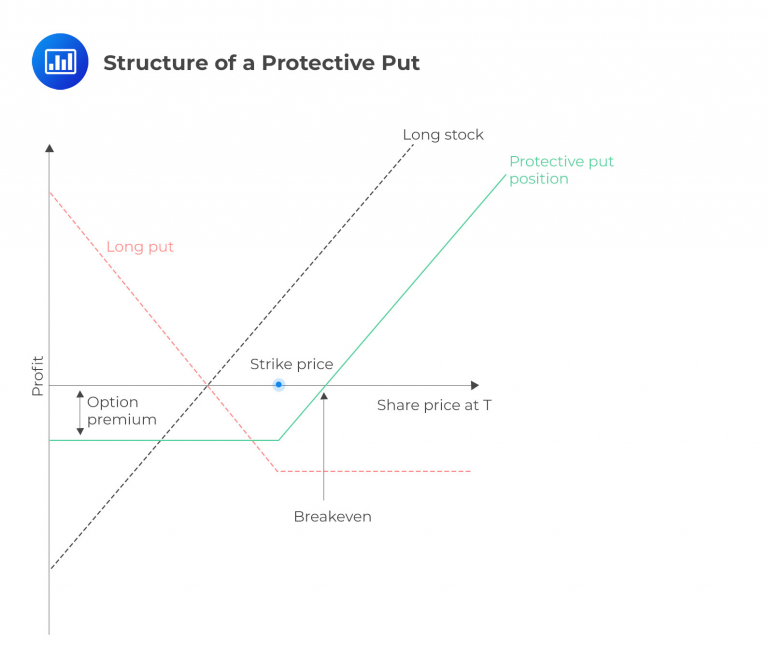
A protective put strategy combines a long stock position with a put option, representing the first half of put-call parity. This combination is sometimes referred to as a married put. The name “protective put” stems from the downside protection the put option provides to the long stock position.

Investors who utilize a protective put strategy are characterized as being cautiously bullish. They believe in the stock’s upside potential and are willing to hold it in their portfolio. However, they may also anticipate short-term volatility or seek to secure previous profits on the shares by employing a put option. A protective put strategy suits investors who maintain a bullish outlook but still exercise caution. 

Structure of a Protective Put

A protective put strategy involves purchasing stock along with a put option at the same time. This combination provides downside protection for the stock position. The figure below illustrates the structure of a protective put strategy.

Let’s consider the BBC example once again. The investor bought BBC stock at $90, which has since risen to $98. The investor is satisfied with this gain and wants to continue holding the shares. However, there is concern about potential volatility due to an upcoming presidential election. To mitigate this risk, the investor purchases a put option with a strike price of $100 and a three-month expiration. The cost of the put option is $2.50. 

The Payoff of Protective Put

In this example of the BBC protective put scenario, let’s analyze the potential payoffs based on the stock price at expiration. The total value of the position at expiration, including the value of the put option, can be calculated as follows:

$$ \text{Price of stock} + \text{value of put} = \text{Total position value} $$

$$ \text{Value of a Put} = \text{Max} (0, \text{Strike} – \text{Stock}) $$

$$ \begin{array}{c|c|c|c} \textbf{Stock price} & \textbf{Value of Put} & \textbf{Value of} & \textbf{Total Value of} \\ \textbf{@ Expiry} & & \textbf{Stock} & \textbf{Position} \\ \hline \$85 & \text{Max}(0, 100-85) = \$15 & \$85 & \$85 + $15 = \$100 \\ \hline \$90 & \text{Max}(0, 100-90) = $10 & \$90 & \$90 + $10 = \$100 \\ \hline \$95 & \text{Max}(0, 100-95) = $5 & \$95 & \$95 + $5 = \$100 \\ \hline \$100 & \text{Max}(0, 100-100) = 0 & $100 & \$100 + 0 = \$100 \\ \hline \$105 & \text{Max}(0, 100-105) = 0 & $105 & \$105 + 0 = \$105 \\ \hline \$110 & \text{Max}(0, 100-110) = 0 & $110 & \$110 + 0 = \$110 \\ \hline \$115 & \text{Max}(0, 100-115) = 0 & $115 & \$115 + 0 = \$115 \end{array} $$

As we can see, the protective put position puts a lower limit on the value of the position itself, hence the term protective put. In no instance can the position’s value be worth less than a combined $100. But consider again that the investor paid a $2.50 premium. Subtracting $2.50 from the value of the position at expiration in a second step is more intuitive for many candidates and allows for the following payoff diagram:

$$ \begin{array}{c|c|c} \textbf{Stock price} & \textbf{Total Value of} & \textbf{Position Value -} \\ \textbf{@ Expiry} & \textbf{Position} & \textbf{Premium} \\ \hline \$85 & \$85 + \$15 = \$100 & \$97.50 \\ \hline \$90 & \$90 + \$10 = \$100 & $97.50 \\ \hline \$95 & \$95 + \$5 = \$100 & \$97.50 \\ \hline \$100 & \$100 + 0 = \$100 & \$97.50 \\ \hline \$105 & \$105 + 0 = \$105 & \$102.50 \\ \hline \$110 & \$110 + 0 = \$110 & \$107.50 \\ \hline \$115 & \$115 + 0 = \$115 & \$112.50 \end{array} $$

The table shows that investors who implement a protective put strategy encounter a minor obstacle in the form of the put premium. However, once the premium is accounted for, they can establish a minimum value for their position while retaining the full potential for upside gains beyond that point.

Risk of Protective Put

Despite its benefits, the protective put strategy has its trade-offs. While it offers an enhanced risk profile compared to holding straight stock, there is a cost associated with purchasing the premium. However, the appeal of the protective put lies in its ability to provide insurance against bear markets. 

Breakeven of Protective Put

Investors may arrive at the breakeven of a protective put with the following formula:

$$ \text{Breakeven at expiration} = (\text{Price paid for stock} + \text{premium paid}) $$

In the example given above, let’s consider an investor who initially purchased BBC stock for $90.00 and subsequently acquired a protective put for $2.50. This raises the effective price of the stock to $92.50, which can be interpreted as the breakeven price for the position.

In summary:

Value at expiration

Total position value = Price of stock + value of put

$$ \text{Total position value } (V_T )= S_T+\text{Max}(0,(K – S_T) $$

Profit

Profit = Value at expiration-initial stock price-put premium

$$ \text{Profit} =V_T-S_0-p_0 $$

Maximum profit

The potential gain of a protective put is unlimited.

$$ \text{Maximum profit} =S_T- S_0 –p_0=\infty $$

Maximum loss

It occurs when the underlying asset is sold at the strike price.

$$ \text{Maximum Loss}=S_0+p_0-K $$

Breakeven of Protective Put

$$ \text{Breakeven at expiration} = \text{Price paid for stock} + \text{premium paid} = S_0+p_0 $$

Question

Which of the following terms from put-call parity most likely represents a protective put position:

1. Stock + Put
2. Call + PV(Strike)
3. Put + PV(Strike)

Solution

The correct answer is A.

It represents a marriage or a protective put strategy.

B is incorrect. This is a fiduciary call. While the payoff is similar to a protective put, they are ultimately two different positions.

C is incorrect. It does not represent one-half of put-call parity.

Reading 17: Options Strategies

Los 17 (c) Discuss the investment objective(s), structure, payoff, risk(s), value at expiration, profit, maximum profit, maximum loss, and the breakeven underlying price at expiration of a protective put position