Credit Default Swap Strategies

A Credit Default Swap (“CDS”) is a tool that allows investors to isolate and manage credit risk apart from other fixed-income risk exposures. As a reminder, credit risk involves the chance of a borrower not repaying funds due.

CDS Mechanics

Contract Diagram at Initiation

Contract Diagram Post-Initiation

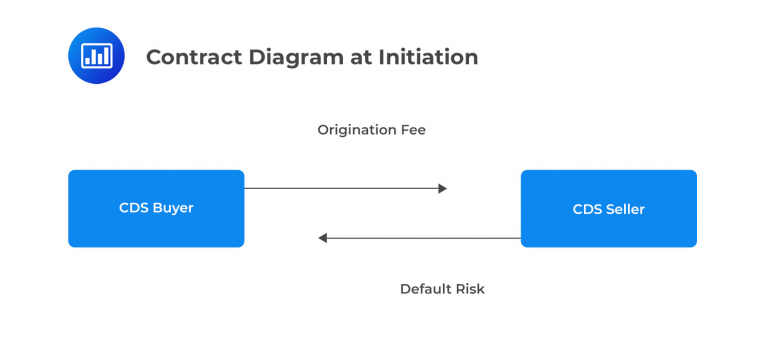
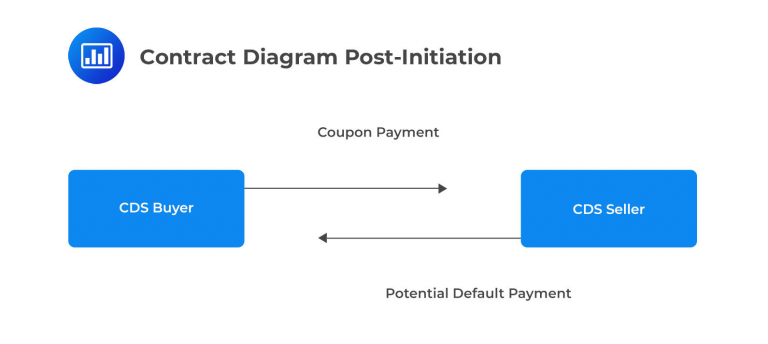
The CDS buyer is essentially buying insurance against potential default losses. In exchange for this insurance, the CDS seller charges an origination fee. This fee is determined using the formula provided below.

CDS Formula

$$ \begin{align*} \text{Price of CDS Insurance} & = ((\text{Fixed Coupon} – \text{CDS Spread}) \\ & \times \text{Effective Spread Duration of CDS}) \end{align*} $$

Where:

CDS Spread = 1% for investment grade issuers and 5% for high-yield issuers were established post-2008 by the International Swaps and Derivatives Association.

The hazard rate is the Probability of the defined ‘credit event’ or the default on payments.

Contract Effective Spread Duration

$$ \frac { \Delta(\text{CDS Price})}{ \Delta(\text{CDS Spread}) }\approx – (\Delta(\text{CDS Spread}) \times \text{EffSpreadDurCDS}) $$

Credit-Based Derivatives Variations

\(\rightarrow\) Single-Name CDS premium paid to the seller in exchange for payment if default occurs.

\(\rightarrow\) Index-based CDS premium paid to the seller in exchange for partial payment if a credit event occurs for the index member.

\(\rightarrow\) Payer Option on CDS Index premium paid to the seller for the right to buy protection (“pay” coupons) on the CDS index contract at a future date.

\(\rightarrow\) Receiver Option on CDS Index premium paid to the seller for the right to sell protection (“receive” coupons) on CDS index contract at a future date.

The CDS Curve is a plot of CDS spreads across the maturity spectrum. This graphic is used to determine pricing for default insurance across time.

Question

An investor wishes to purchase credit protection under a ten-year CDs contract. The covered firm is considered to have a low risk of default. Calculate the upfront premium.

$$ \begin{array}{l|r} \textbf{Market spread} & 0.25\% \\ \hline \textbf{Effective spread duration} & 6.22 \\ \hline \textbf{Investment-grade coupon} & 1.00\% \\ \hline \textbf{High-yield coupon} & 5.00\% \end{array} $$

1. 4.665%.
2. -29.545%.
3. 29.545%.

Solution

The correct answer is A.

Formula \(\rightarrow\)

$$ \begin{align*} \text{Price of CDS} = & ((\text{Fixed Coupon} – \text{CDS Spread}) \\ \times & \text{Effective Spread Duration of CDS}) \\ & ((1.00\% – 0.25\%) \times 6.22)) = 4.665\% \end{align*} $$

B and C are incorrect. Both solutions, B and C, use the high-yield coupon and/or confound the premium as a net payment vs. a net receipt.

$$ ((5.00\% – 0.25\%) \times 6.22)) = 29.545\% $$

Reading 22: Fixed Income Active Management: Credit Strategies

Los 22 (g) Discuss the use of credit default swap strategies in active fixed-income portfolio management