The expected return on a fixed-income portfolio is given by:
\(E(R) \approx\) Coupon income
+/− Rolldown return
+/− E(\(\Delta\) Price due to investor’s view of benchmark yields)
+/− E(\(\Delta\) Price due to investor’s view of yield spreads)
+/− E(\(\Delta\) Price due to investor’s view of currency value changes)
E(R) represents the expected return on the portfolio. The variables represent different components of the return. ‘Coupon income’ refers to the periodic interest payments received from the bond. ‘Rolldown return’ refers to the gain or loss due to the passage of time. The terms with ‘E’ represent the expected changes in price due to the investor’s views on different factors: benchmark yields, yield spreads, and currency value changes.
Yield Curve Dynamics
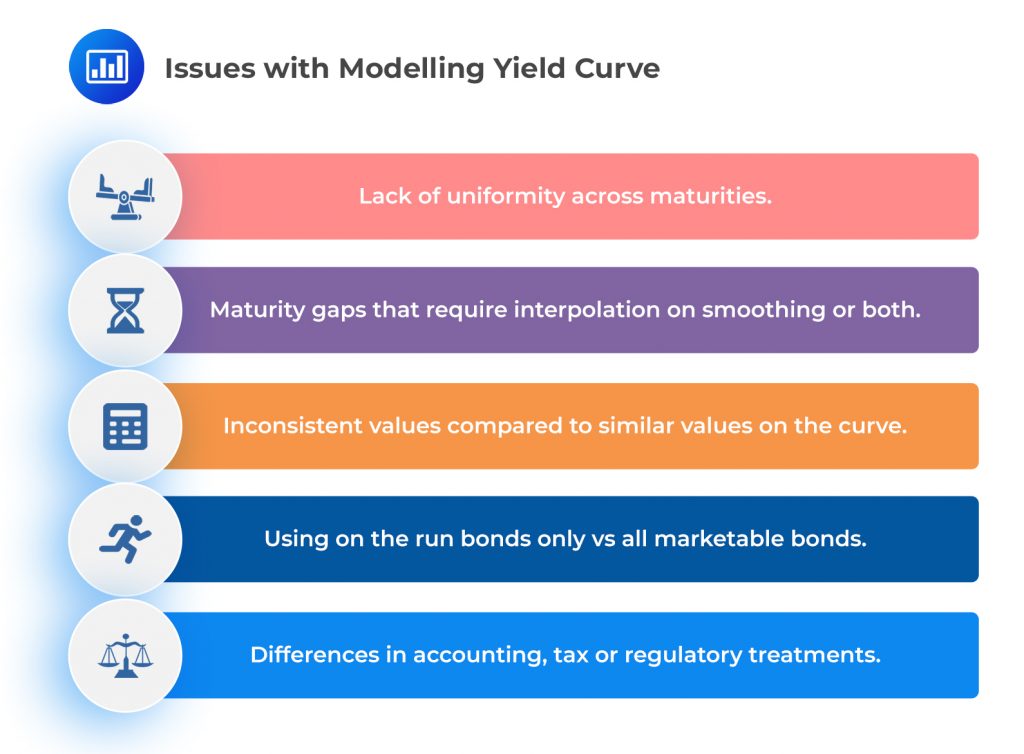
Yield Curve Dynamics focuses on graphical representation of yields-to-maturity for various maturities of a specific issuer or group of issuers. It is important to note that yield curve models are based on certain assumptions that may vary depending on the investor or the intended use of the curve.
For instance, consider the yield curves of the most recently issued, or on-the-run, securities. These may differ significantly from those that include off-the-run securities, which are typically less liquid and hence have a lower price (higher yield-to-maturity). This difference can cause the yield curve to skew higher.
It’s also crucial to understand that reported yield curves often do not consist of traded securities and must be derived from available bond yields-to-maturity using a model. This is particularly true for constant maturity yields, which estimate what a hypothetical yield-to-maturity would be if a bond were available with a specific maturity. Different models and assumptions can produce different yield curves.
The difference between models becomes more pronounced as yields-to-maturity are converted to spot and forward rates. A tradeoff exists between yield-to-maturity and liquidity, which active management strategies must assess when selecting bonds for the portfolio.
Primary yield curve risk factors are often categorized by three types: a change in (1) level (a parallel “shift” in the yield curve); (2) slope (a flattening or steepening “twist” of the yield curve); and (3) shape or curvature (or “butterfly movement”). These factors are of utmost importance in realizing excess portfolio returns under an active yield curve strategy.
Yield Curve Factors
Between 2007 and 2020, the 10-year US Treasury yields-to-maturity experienced significant fluctuations, hitting record lows in 2020 due to the COVID-19 pandemic. This era was characterized by slower economic growth and an accommodative monetary policy, including quantitative easing by global central banks. This led to government yields falling to zero and even below. In 2020, negative yields were a common feature on many Japanese, German, and Swiss government bonds.
Yield Level Change
A change in yield level, also known as a parallel shift, occurs when all yields-to-maturity represented on the curve change by the same number of basis points. Portfolio managers often use a first-order duration statistic to estimate the impact of an expected yield curve change on portfolio value. However, this method assumes that yield curve changes occur only in parallel shifts, which is not reliable when the yield curve’s slope and curvature also change. For larger yield curve changes, second-order effects should be included to better measure changes in portfolio value.
Yield Curve Slope
The slope of the yield curve is typically defined as the difference in basis points between the yield-to-maturity on a long-maturity bond and the yield-to-maturity on a shorter-maturity bond. As the spread between these two yields increases or widens, the yield curve is said to steepen. Conversely, a decrease or narrowing in the spread is referred to as a flattening of the yield curve. In most cases, the spread is positive and the yield curve is upward-sloping. If the spread turns negative, the yield curve is described as “inverted.”
Yield Curve Shape or Curvature
The shape or curvature of the yield curve is the relationship between yields-to-maturity at the short end of the curve, at a midpoint along the curve (often referred to as the “belly” of the curve), and at the long end of the curve. A common measure of yield curve curvature is the butterfly spread, which indicates a difference between medium-term yields and a linear interpolation between short-term and long-term yields-to-maturity. A positive butterfly spread indicates a “humped” or concave shape to the midpoint of the curve, while a “saucer” or convex shape indicates the spread is negative.
$$ \begin{align*} \text{Butterfly Spread} & = – (\text{Short-term yield}) + (2 \times \text{Medium-term yield}) \\ & – \text{Long-term yield} \end{align*} $$
The short-term yield, medium-term yield, and long-term yield represent the yields-to-maturity at the short end, midpoint, and long end of the yield curve, respectively. The butterfly spread takes on larger positive values when the yield curve has more curvature.
Duration and Convexity
Active managers of fixed-income portfolios aim to leverage expected changes in the level, slope, and curvature of the benchmark yield curve to maximize returns. They focus on the anticipated change in portfolio value due to yield-to-maturity changes. This term combines the effects of duration and convexity, two key factors that establish the price/yield relationship for fixed-income bonds.
Duration, a negative, linear first-order factor, attempts to capture a linear relationship between bond prices and yield-to-maturity. Convexity, a usually positive, non-linear second-order factor, describes a bond’s price behavior for larger movements in yield-to-maturity. This additional term is a positive amount on a traditional (option-free) fixed-rate bond for either a yield increase or decrease, causing the yield/price relationship to deviate from a linear relationship.
Active managers focus on the incremental effect on these summary statistics for a portfolio by adding or selling bonds in the portfolio or by buying and selling fixed-income derivatives. They often approximate changes in a bond portfolio’s present value (PV) by substituting market value (MV)-weighted averages for modified duration and convexity into Equation 3.
Duration management—accounting for changes in yield curve level—will usually be a more important consideration for portfolio performance than convexity management. This is consistent with the relative importance of the yield curve level, slope, and curvature. Convexity management is more closely associated with yield curve slope and shape changes.
Positive convexity is a valuable feature in bonds. If a bond has higher positive convexity than an otherwise identical bond, then the bond price increases more if interest rates decrease (and decreases less if interest rates increase) than the duration estimate would suggest.
The expected price of a bond with positive convexity for a given rate change will be higher than the price change of an identical-duration, lower-convexity bond. This price behavior is valuable to investors; therefore, a bond with higher convexity might be expected to have a lower yield-to-maturity than a similar-duration bond with less convexity.
Convexity Effect
Convexity effect can be seen by comparing two bond portfolios: The first portfolio concentrated in a single intermediate maturity is often referred to as a bullet portfolio. The second portfolio, with similar duration but combining short- and long-term maturities, is a barbell portfolio. Although the bullet and barbell have the same duration, the barbell’s higher convexity results in a larger gain as yields-to-maturity fall and a smaller loss when yields-to-maturity rise.
$$ \%\Delta PV_{Full} \approx −(\text{ModDur} \times \Delta \text{Yield}) + \left[\frac{1}{2} \times \text{Convexity} \times (\Delta \text{Yield})^2 \right]$$
$$\text{AvgModDur} = \sum_{j=1}^{J} \text{ModDur}_j \times \left(\frac{MV_j}{MV}\right) .$$
$$\text{AvgConvexity} = \sum_{j=1}^{J} \text{Convexity}_j \times \left(\frac{MV_j}{MV}\right) .$$
Practice Questions
Question 1: In the context of fixed-income portfolio returns, the expected return, denoted as E(R), is a sum of several components. These components are crucial in determining the overall performance of the portfolio. If an investor is actively managing their portfolio, they need to have a clear understanding of these components and how they interact with each other. Which of the following is NOT a component of the expected return on a fixed-income portfolio as per the curriculum?
- Coupon income
- Changes in price due to the investor’s view of benchmark yields
- Changes in stock market indices
Answer: Choice C is correct.
Changes in stock market indices are NOT a component of the expected return on a fixed-income portfolio. Fixed-income portfolios are composed of debt securities such as bonds, which pay a fixed or variable interest rate to the investor. The performance of these portfolios is primarily influenced by factors such as the coupon income, changes in the bond’s price due to changes in interest rates, and the investor’s view of benchmark yields. The stock market indices, on the other hand, track the performance of a specific basket of stocks and are not directly related to the performance of a fixed-income portfolio. While changes in stock market indices might indirectly affect the fixed-income market through changes in the overall economic environment, they are not a direct component of the expected return on a fixed-income portfolio.
Choice A is incorrect. Coupon income is indeed a component of the expected return on a fixed-income portfolio. It represents the periodic interest payments that the investor receives from the issuer of the bond. This is a crucial component of the total return from a fixed-income investment.
Choice B is incorrect. Changes in price due to the investor’s view of benchmark yields is also a component of the expected return on a fixed-income portfolio. If an investor believes that benchmark yields will decrease, they may expect the price of their bonds to increase, contributing to a higher total return. Conversely, if they expect yields to increase, they may anticipate a decrease in the price of their bonds, which would lower the total return.
Question 2: The curriculum delves deeper into the active management of certain components of the expected return on a fixed-income portfolio. Active management is dependent on the investor’s ability to identify actionable trades with specific securities. Which of the following sections of the curriculum does NOT focus on the active management of the components of the expected return?
- Section 2 and 3, focusing on coupon income, rolldown return, and changes in price due to the investor’s view of benchmark yields
- Section 4, incorporating changes in currency value
- Section 5, focusing on changes in stock market indices
Answer: Choice C is correct.
Section 5, focusing on changes in stock market indices, does not focus on the active management of the components of the expected return on a fixed-income portfolio. Active management in a fixed-income portfolio involves making investment decisions based on the analysis of various factors such as interest rates, credit risk, and currency risk. These factors directly impact the components of the expected return on a fixed-income portfolio, which include coupon income, price change due to changes in interest rates, and reinvestment income. Changes in stock market indices, on the other hand, are more relevant to equity portfolios rather than fixed-income portfolios. While changes in stock market indices may indirectly affect fixed-income securities, they are not a direct component of the expected return on a fixed-income portfolio. Therefore, a section focusing on changes in stock market indices would not be directly related to the active management of the components of the expected return on a fixed-income portfolio.
Choice A is incorrect. Section 2 and 3, focusing on coupon income, rolldown return, and changes in price due to the investor’s view of benchmark yields, are directly related to the active management of the components of the expected return on a fixed-income portfolio. These sections focus on the analysis and management of key components of the expected return, including coupon income and price changes due to changes in interest rates.
Choice B is incorrect. Section 4, incorporating changes in currency value, is also related to the active management of the components of the expected return on a fixed-income portfolio. Changes in currency value can significantly impact the return on a fixed-income portfolio, especially for portfolios that include foreign currency-denominated bonds. Therefore, active management of currency risk is a key aspect of managing the expected return on a fixed-income portfolio.
Glossary
- Coupon income: The periodic interest payments received from the bond.
- Rolldown return: The gain or loss due to the passage of time.
- Benchmark yields: The standard against which the performance of a security, mutual fund or investment manager can be measured.
- Yield spreads: The difference between yields on differing debt instruments, calculated by deducting the yield of one instrument from another.
- Currency value changes: The fluctuation in the value of one currency relative to another currency.
- Duration: A measure of the sensitivity of the price of a bond to a change in interest rates.
- Convexity: A measure of the curvature in the relationship between bond prices and bond yields.
- Yield-to-Maturity (YTM): The total return anticipated on a bond if it is held until it matures.
- Market Value (MV): The current price at which an asset can be bought or sold.
- Constant maturity yields: Hypothetical yield-to-maturity estimates for bonds with a specific maturity.
Portfolio Management Pathway Volume 2: Learning Module 5: Yield Curve Strategies;
LOS 5(a): Describe the factors affecting fixed-income portfolio returns due to a change in benchmark yields