Pricing and Valuation Concepts

A forward commitment is a derivative contract that allows one to buy or sell an underlying security at a predetermined price at a future date.

The price of a forward or a futures contract is the prespecified price that the buyer (long position holder) should pay the seller (short position holder) to purchase the underlying asset at the expiration/settlement date. On the other hand, the value of a forward or futures contract is the current monetary value determined after contract inception.

Arbitrage Free Pricing and Valuation of Forward Commitments

Forward commitments pricing and valuation concepts are based on the no-arbitrage approach, meaning that prices adjust to not follow arbitrage profits. An arbitrageur is therefore bound to follow two fundamental rules:

• Do not use your own money – the arbitrageur borrows money to purchase the underlying and invests proceeds from short-selling transactions at the risk-free rate.
• Do not take any price risk – the arbitrageur eliminates any market price risk related to the underlying and the derivatives used

Example: No-arbitrage Approach

An investor goes short a September E-Mini S&P 500 futures contract on 30 October 2020 for $3,225. The initial value of this contract is $0. On the following trading day (02 November 2020), the E-Mini futures contract price increases to $3,324. The short investor’s position now has a negative value of $99.

The no-arbitrage principle argues that it is impossible to generate money today without the risk or future liability. In other words, there is no way an investor can combine a forward contract position and another asset to generate riskless profits. The following can be deduced from the no-arbitrage principle:

• Two portfolios with identical future cash flows, regardless of future events, should have the same price (Law of one price)
• The portfolio should yield a risk-free rate of return, if it generates certain payoffs 

Forward Pricing

Pricing a forward contract is the process of determining the no-arbitrage price that will make the value of the contract zero to both parties at the contract’s initiation.

The forward price is the price that would not permit profitable riskless arbitrage in frictionless markets. In other words, it is the spot price compounded at the risk-free rate over the life of the contract.

$$F_{0}(T)=S_{0}\times(1+r_{f})^{T}$$

or

$$S_{0}=\frac{F_{0}(T)}{(1+r_{f})^{T}}$$

Where: 

\(F_{0}(T)\)= Future price

\(S_{0}\)= Spot price at the start of the contract of the underlying asset

\(r_{f}\)= risk-free rate of interest

\(\text{T}\)= term of the forward contract

Example: Calculating the Forward Price

Given an asset priced at $130 and a risk-free annual rate of 4%. The one-year forward price is closest to:

$$F_{0}(T)=S_{0}\times(1+r_{f})^{T}$$

$$F_{0}(1)=130\times(1+4\%)^{1}=$135.20$$

Forward Arbitrage

An arbitrage opportunity exists when:

$$F_{0}(T)≠FV(S_{0})$$

Where:

\(F_{0}(T)\) is the forward price 

\(FV(S_{0})=S_{0}(1+r_{f})^{T}\)

If  \(F_{0}(T)>FV(S_{0})\), the arbitrageur shorts the forward contract and longs the underlying instrument. This means that the forward price is driven down, and the underlying price is driven up until \(F_{0}(T)=FV(S_{0})\) and a riskless gain today no longer exists.

If , \(F_{0}(T)<FV(S_{0})\), the arbitrage trader buys the forward contract and shorts the underlying. Arbitrageurs drive the forward prices to equal the future value of the underlying, effecting the law of one price.

a) Carry Arbitrage

Carry arbitrage occurs when the forward contract is overpriced.

I.e. 

$$F_{0}(T)>S_{0}\times(1+r_{f})^{T}$$

Thus, the arbitrageur is long (carries) the underlying asset and shorts the forward contract.

Example: Carry Arbitrage

An asset is priced at $130, and the risk-free annual rate is 4%. If the forward price, F₀(T), is $140, then there is an opportunity for carry arbitrage.

The one-year forward price is:

$$F_{0}(T)=S_{0}\times(1+r_{f})^{T}$$

$$F_{0}(1)=130\times(1.04)^{1}=$135.20$$

The arbitrageur can make a riskless profit as follows:

Cash flows at contract initiation 

• Short the forward contract on the underlying at $140
• Borrow +$130 at the risk-free rate
• Purchase the underlying with the loan –$130
• Borrow the arbitrage profit:

$$+PV\bigg[F_{0}(T)-S_{0}(1+r_{f})^{T}\bigg]=+PV[$140-$135.20]=+\frac{$4.8}{1.04}=+$4.615$$

Initial Cash Flow \(=-$130+$130+$4.62=+$4.62\)

Cash flows at time T 

• Deliver the underlying to the short party for \(+$140\)
• Repay the loan amount of \((130+4.62)\times(1.04)=-$140\)
• Cash Flow at time \(T=-$140+$140=$0\)

b) Reverse Carry Arbitrage 

In a reverse carry arbitrage, the holder is short the underlying asset and long the forward contract. This is because the forward contract is underpriced.

$$F_{0}(T)<FV(S_{0})$$

Example: Reverse Carry Arbitrage

Consider an asset priced at $130. The risk-free annual rate is 4%. If the forward price, \(F_{0}(T)\), is $115, then there is an opportunity for reverse carry arbitrage.

$$\text{Forward price} (F_{0}(T))=S_{0}\times(1+r_{f})^{T}$$

$$F_{0}(1)=130\times(1.04)^1=$135.20$$

At contract initiation

• Long the forward contract on the underlying at $130
• Short-sell the underlying at $130
• Lend the funds for the underlying purchase: –$130
• Borrow the arbitrage profit:

$$+PV[FV(S_{0})-F_{0}(T)]=+PV[$135.20-$130]=\frac{+5.20}{(1.04)}=+$5$$

• Cash Flow at time 0: \(+$130-$130+$5.00=+$5.00\)

Cash Flow at time T

• Collect loan: \(($130)(1.04)=+$135.20\)
• Repay:\(-$5.00(1.04)=-$5.20\)
• The long party delivers –$130 on the underlying
• Cover the short asset position
• Cash Flow (at time T): \(+$135.20–$5.20–$130=$0\)

Valuing a Forward Contract

Consider a forward contract whose underlying has no cashflows:

At the contract initiation, (Time  = 0), the value to the long position in a forward contract is:

$$V_{0}=S_{0}-\frac{F_{0}(T)}{(1+r_{f})^{T}}$$

The forward value at time t to the long position in the forward contract entered at time 0 is the discounted value of the difference between the forward prices. I.e.

$$V_{t}(T)=\frac{[F_{t}(T)-F_{0}(T)]}{(1+i)^{T-t}}$$

Note that the forward contract has no value at a time (0) to both the long and short positions.

Example: Calculating the value of a Forward Contract whose underlying has no cashflows

An investor purchases a long one-year forward contract at $130. Three months later, the contract’s price increases to $132.

Given that the risk-free rate is 4%, the value of the long forward position is closest to:

$$V_{t}(T)=[F_{t}(T)-F_{0}(T)](1+i)^{-T-t}$$

$$Vt(T)=\frac{$132-$130}{(1.04)^{\frac{9}{12}}}=$1.9420$$

Equity Forward Contracts

Pricing of Equity Forwards

A stock or an equity index may have expected periodic payments (dividends) during the life of the contract. The forward pricing formula can be adjusted to account for such payments. Generally, these periodic payments include carry benefits such as dividends,  interest, or coupon payments and carry costs such as interest rate (opportunity cost) and storage related to the underlying instrument.

Carry costs increase the burden of carrying the underlying instrument with time and thus are added to the forward pricing equation. On the other hand, benefits lower the burden of carrying the underlying instrument with time. Therefore, they are subtracted in the forward pricing equation.

Equity Forward Contracts with Discrete Cashflows

The no-arbitrage forward price of a dividend-paying stock is given by:

$$F_{0}(T)=[S_{0}-(\gamma-\theta)](1+r_{f})^{T}$$

Where:

\(F_{0}(T)\):  The forward price

\(S_{0}\): The initial price of the underlying asset 

\(T\): The time to expiry

\(r_{f}\): The risk-free rate of interest

\(\theta\): Present value of costs to hold the spot asset. These may include storage and/or insurance

\(\gamma\): Present value of benefits of holding the spot asset include dividends, interest 

Thus, the forward price of an asset with benefits and/or costs is the spot price compounded at the risk-free rate over the life of the contract minus the future value of those benefits and costs.

Example 1: Calculating the price of an equity forward contract when the Underlying has Discrete Cashflows

Consider a stock whose current price is $50. The stock is expected to pay a dividend of $1 in 30 days and 90 days from today. The price of a 70-day forward contract when the interest rate is 4% is closest to:

$$F_{0}(T)=[S_{0}-(\gamma-\theta)](1+r_{f})^{T}$$

$$\theta=\frac{1}{1(.04)^{\frac{30}{365}}}=0.9968$$

$$F_{0}(T)=[$50-($0.9968-0)](1.04)^{\frac{70}{365}}=$49.37$$

Example 2: Calculating the price of an equity forward contract when the Underlying has Discrete Cashflows

Suppose that the spot price of the underlying asset at time 0, \(S_{0}=$100\). The asset pays a $2 dividend in 6 months, and the risk-free rate is 8%. The one-year forward price is closest to:

$$F_{0}(T)=[S_{0}-(\gamma-\theta)](1+r_{f})^{T}$$

Solution

Note that  and  are the present values of the carry benefits (dividends) and carry costs (coupon payments)

$$\gamma=2(1.08)^{-\frac{6}{12}}=$1.9245$$

$$\theta=0$$

$$F_{0}(T)=[100-(1.9245-0)](1+0.08)^1=$105.92$$

Equity Forward Contracts with Continuous Cashflows

Stock indexes with many stocks, such as the S&P 500, assume that dividends are continuously compounded. The dividends are the benefits of carry. The forward price at time 0 is thus expressed as:

$$F_{0}(T)=S_{0}e^{(r_{c}+\theta-\gamma)\times{T}}$$

Where: 

\(S_{0}=\) price of the underlying 

\(r_{c}=\) Continuously compounded risk-free rate of interest

\(\theta=\) Present value of costs of carry

\(\gamma=\) Present value of carry benefits

Example: Calculating the Price of an Equity Forward Contract whose underlying has continuous cash flows

The Dow Jones index (DJ30) is trading at a spot price of $30,125.

The index pays a continuous dividend of 3%. If the continuously compounded risk-free rate is 2%, the six-month forward price is closest to:

Formula:

$$F_{0}(T)=S_{0}e^{(r_{c}+\theta-\gamma)\times{T}}$$

$$F_{0}(T)=30,125\times e^{(0.02+0-0.03)\times0.5}$$

$$F_{0}(T)=$29, 974.75$$

Equity Forward Contract Valuation when the Underlying has Discrete Payments

An equity forward value is determined as the difference between the spot price of the underlying asset and the present value of the remaining expected dividend payments and the forward price. This is expressed mathematically as:

$$V_{t}(T)=S_{t}-(\gamma-\theta)(1+r)^{t}-F_{0}(T)(1+r)^{-T-t}$$

Where: 

\(V_{t}(T)\)= the forward contract value at time t

\(S_{t}\)= Spot price at time t

\(F_{0}(T)=\) Forward price agreed upon at contract initiation

\(t=\) Some point in time after the contract is initiated and before it expires

\((T-t)=\) Remaining time to expiration

\(\gamma=\) Carry benefits (e.g., dividends)

\(\theta=\) Carry costs 

Example: Determining the value of an Equity Forward

The current price of a stock is $50. The stock is expected to pay a dividend of $1 in 30 days and 90 days from today. Assume that after 40 days, the stock price is $40, and the risk-free rate 4%. The value of the stock forward contract to the long position is closest to:

We first calculate the forward price of the contract:

$$F_{0}(T)=[S_{0}-(\gamma-\theta)](1+r_{f})^{T}$$

$$\gamma=1(1.04)^{-\frac{30}{365}}=0.9968$$

$$F_{0}(T)=[$50-($0.9968-0)](1.04)^{\frac{70}{365}}=$49.37$$

Note that the dividend received after 90 days is not included in this calculation as the forward contract will have expired by then.

The value of the forward contract is then calculated using the formula:

$$V_{t}(T)=S_{t}-(\gamma-\theta)(1+r)^{t}-F_{0}(T)(1-r)^{-(T-t)}$$

$$V_{t}(t)=40-\frac{49.37}{(1.04)^{\frac{30}{365}}}=-$9.21$$

The forward contract value on the stock to the long position is (-)$9.21. This means that the value of the forward contract on the stock to the short position is (+)$9.21.

Forward and Future Contracts on Fixed Income Bonds

Forward Contracts on Fixed Income Bonds

The pricing and valuation of a coupon paying bonds is similar to that of dividend-paying stocks. However, the cash flows, in this case, are coupons and not dividends.

Price of a forward on a fixed-income security

$$F_{0}(T)=(S_{0}-PVC_{0})\times(1+r_{f})^{T}$$

Where: 

\(F_{0}(T)\) is the forward price

\(S_{0}\) is the spot price

\(PVC_{0}\) is the present value of coupon payments

\(r_{f}\) is the risk-free rate of interest

\(T\) is the term of the contract

Example: Calculating the Price of a fixed-income security forward

Consider the following information relating to a forward contract on a fixed coupon bond:

$$\small{\begin{array}{|l|c|}\hline\text{Forward contract duration (days)} & 200 \\ \hline\text{Par value} & \$100 \\ \hline\text{Coupon rate} & 4.0\% \\ \hline\text{Payment Frequency} & \text{semi-annual} \\ \hline \text{Spot price} & \$110.00\\ \hline\text{Risk-free rate} & 8.0\% \\ \hline\text{Time until next coupon payment} & 160 \\ \hline\text{Coupon payment} & \$2.00 \\ \hline\text{The present value of coupons (PVC)} & \$1.93\\ \hline\textbf{Forward Price} & \textbf{\$112.72}\\ \hline\end{array}}$$

The calculations are as follows: 

$$\text{Coupon payment}=4\%\times0.5\times100=$2$$

$$\text{Present value of coupon payment}=\frac{2}{(1.08)^{\frac{160}{365}}}=$1.93$$

$$\text{Forward price}=(110-1.93)\times(1.08)^{\frac{200}{365}}=$112.72$$

Value of a fixed income security Forward Contract

The value of a fixed income forward contract at any given time, t, before expiration is given as:

$$V_{t}(Long)=(S_{t}-PVC_{t})-\frac{F_{0}(T)}{(1+r_{f})^{T-t}}$$

Alternatively, if given the current forward price \(F_{t}(T)\) on the same underlying and identical maturity:

$$V_{t}(Long)=PV_{(t,T)}[F_{t}(T)-F_{0}(T)]$$

Example: Calculating the value of  a fixed-income security forward

Consider a $100 par, 4% semi-annual coupon bond with a spot price of $100 that matures in 200 days. The bond has just made a coupon payment until the next coupon payment is 160 days. After 120 days, the value of the bond is $127.

Given that the risk-free rate of interest is 8%, the value of the forward contract on the bond to the long position is closest to:

Solution

$$\text{Coupon payment}=4\%\times0.5\times100=$2$$

$$\text{Present value of coupon payment}=\frac{2}{(1.08)^{\frac{160}{365}}}=$1.93$$

$$F_{0}(T)=(110-1.93)\times(1.08)^{\frac{200}{365}}=$112.72$$

$$V_{t}(Long)=(S_{t}-PVC_{t})-\frac{F_{0}(T)}{(1+r_{f})^{T-t}}$$

After 120 days, only one coupon payment is due in 40 days (160-120) before the contract maturity in 80 days (200-120).

$$PVC_{t}=\frac{2}{(1.08)^{\frac{40}{365}}}=$1.9832$$

$$V_{120}(Long)=$127-1.9832-\frac{$112.72}{(1.08)^{\frac{80}{365}}}=$14.18$$

Future Contracts on Fixed Income Bonds

The bond price is usually quoted as a clean price in some countries. This means that the bonds’ prices are quoted without the interest that has accrued since the last coupon date. The quoted price is sometimes known as the clean price.

$$\text{Clean price}=\text{Full price}-\text{Accrued interest (AI)}$$

Where:

$$\text{AI}=\frac{\text{Days since last coupon payment}}{\text{Days between coupon payments}}\times\text{Coupon amount}$$

Bond futures have more than one bond that can be delivered by the seller (short). When multiple bonds can be delivered for a particular maturity of a futures contract, a cheapest-to-deliver bond normally emerges after adjusting for the conversion factor.

Thus, we can define bond futures as financial derivatives that give the seller (short) an option to select the bond to deliver, which satisfies the contract’s delivery terms.

Each bond is given a conversion factor (CF), which is used to determine the final delivery price.

The buyer pays the futures price multiplied by the conversion factor at expiration.

The futures price, \(F_{0}(T)\), of a fixed income forward or futures contract is the quoted futures price, \(QF_{0}(T)\), times the conversion factor, \(CF(T)\).

$$F_{0}(T)=QF_{0}(T)CF(T)$$

Price of a Bond Futures Contract

According to the carry arbitrage model, futures price must equal the future value of the underlying adjusted for any carry costs or benefits to eliminate arbitrage opportunities at equilibrium.

Thus,

$$F_{0}(T)=FV_{0,T}(S_{0})-AI_{T}-FVCI_{0,T}$$

Where:

\(AI_{T}=\) Accrued interest at maturity of the futures contract

The conversion factor adjusted future value of the underlying adjusted for carry benefits and costs is given as follows:

$$QF0(T)=\bigg[\frac{1}{CF(T)}\bigg]\times(FV_{0,T}[B_{0}(T+Y)+AI_{0}]-AI_{T}-FVCI_{0,T})$$

Example: Calculating Equilibrium Bond Futures Price

The following information relates to a six months Euro bond futures contract with a value of €50,000. The underlying is a 5% bond quoted at €110 with an accrued interest of €1.00. Suppose that there are no coupon payments due until after the futures contract expires.

Futures Contract

$$\small{\begin{array}{|l|c|}\hline\text{Euro bond Contract Value} & €50,000 \\ \hline\text{Conversion factor} & 0.65 \\ \hline\text{Time to contract expiration} & 0.5 \\ \hline\text{Accrued interest over the life of futures contract} & 0 \\ \hline\text{Risk-free rate} & 4.00\%\\ \hline\end{array}}$$

Underlying Bond

$$\begin{array}{|l|c|}\hline\text{Quoted Bond price} & €110 \\ \hline\text{Accrued interest since last coupon payment} & € 1.00 \\ \hline\text{Accrued interest at futures contract expiration} & € 3.00\\ \hline\end{array}$$

The equilibrium bond futures price based on the carry arbitrage model is closest to:

$$QF0(T)=\bigg[\frac{1}{CF(T)}\bigg]\times(FV_{0,T}[B_{0}(T+Y)+AI_{0}]-AI_{T}-FVCI_{0,T})$$

Where: 

\(T=(6/12)\)

\(CF(T)=0.65\)

\(B_{0}(T+Y)= €110\)

\(FVCI_{0,T}=0\)

\(AI_{0}=€1.00\)

\(AI_{T}=€3.00\)

\(r=4\%\)

Thus, 

$$QF_{0}(T)=\bigg[\frac{1}{0.65}\bigg]\times[(110+1)\times(1.04)^{0.5}-3-0]=€169.54$$

Value of a Bond’s Future Contract

The value of a bond future is the change in price since the previous day’s settlement. This is because bond futures are marked to market. The futures value is captured at the end of the day during the bond settlement, at which time the value of the contract is zero.

Interest Rate Forward and Futures Contracts

The London Interbank Offered Rate (LIBOR) is a widely used interest rate used as the underlying derivative contracts. It represents the rate at which London banks can borrow from each other, and it is quoted as an annualized rate based on a 360-day year. The Eurodollar deposit is used for deposits in large banks outside the united states, denominated in U.S. dollars.

Forward Rate Agreements (FRAs)

FRAs are forward contracts with an interest rate, such as LIBOR as the underlying. These contracts allow the counterparties to make a known interest payment at a future date and receive an unknown interest payment in return.

An FRA has two counterparties: the short (fixed receiver) and the long (floating receiver).

The short (lender) receives an interest payment based on the fixed rate and makes an interest payment based on the floating rate. On the other hand, the long (borrower) receives an interest payment based on the floating rate and makes an interest payment based on the fixed rate—the floating receiver gains when LIBOR rises.

FRAs are cash-settled, implying that money is not lent or borrowed.

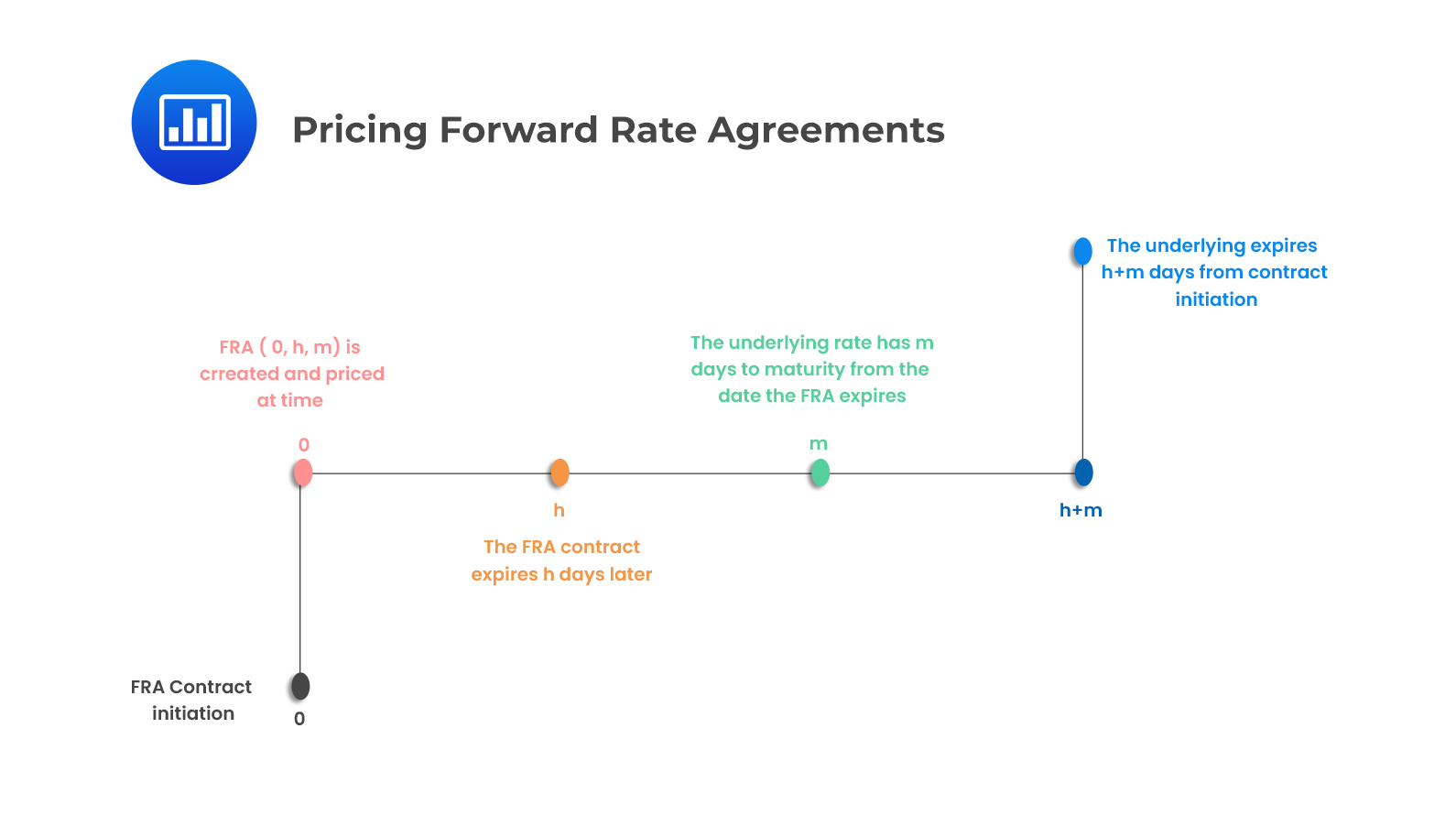
FRAs are identified using “\(\text{X}\times\text{Y}\)” convention, where X shows the point where the FRA expires and the underlying loan starts. On the other hand, Y shows the point where the underlying loan ends.

For example, a \(6\times9\) FRA:

• Is a forward contract that expires in 6 months
• The underlying loan is settled in 9 months
• The notional loan period is three months
• The payoff of the FRA is determined by a three-month Libor when the FRA expires in 6 months.

An \(\text{X}\times\text{Y}\) FRA can also be denoted by FRA (0, h, m), which is interpreted as the fixed forward rate set at time 0 that expires at time h where the underlying Libor deposit has m days to maturity at the expiration of the FRA.

Thus, a \(6\times9\) FRA can be expressed as FRA (0,180,90)

FRA Settlement

Settlement of derivative contracts can be done in the following ways:

Advanced set: The reference interest rate is set when the money is deposited at the FRA expiration date, h, which is the time the underlying loan starts.

Advanced settled: The settlement is made at time h

Settled in arrears: Interest is paid at time \(h+m\) when the underlying loan matures.

FRAs are usually settled based on an advanced set, advanced settled. On the other hand, swaps and interest rate options are normally based on an advanced set, settled in arrears.

Pricing Forward Rate Agreements

The appropriate FRA (0,h,m) rate must be determined when pricing an FRA. This is the rate that makes the FRA’s value equal to zero at the start of the contract.

The FRA fixed rate is determined using the formula:

$$FRA(0,h,m)=\bigg(\frac{1+L_{0}(h+m)t_{h+m}}{[1+L_{0}(h)t_{h}]}-1\bigg)/t_{m}$$

The above formula is read as the compound value of $1 invested at the longer-term Libor for h + m days divided by the compound value of $1 invested at the shorter-term Libor for h days, minus one and then annualized.

In simple terms, the price of an FRA is determined using the following steps:

i. Create a timeline

ii. De-annualize the fixed rate: \(\frac{1+L_{0}(h+m)t_{h+m}}{[1+L_{0}(h)t_{h}]}-1\)

iii. Annualize the fixed rate: \(\bigg[\frac{1+L_{0}(h+m)t_{h+m}}{[1+L_{0}(h)t_{h}]}-1\bigg]\times\frac{360}{m}\)

Notice that the annualization has been done by multiplying by \(\frac{360}{m}\)

Example: Calculating the Price of an FRA

The \(1×6\) fixed FRA rate given a current 30-day LIBOR of 2% and 180- day LIBOR of 3.5% assuming a 30/360-day count convention is closest to:

$$FRA(0,h,m)=\bigg(\frac{1+L_{0}(h+m)t_{h+m}}{[1+L_{0}(h)t_{h}]}-1\bigg)/t_{m}$$

$$FRA(0,30,150)=\bigg(\frac{1+L_{0}(180)t_{180}}{[1+L_{0}(30)t_{30}]}-1\bigg)/t_{150}$$

$$\bigg(\frac{1+0.035\times\frac{180}{360}}{1+0.02\times\frac{30}{360}}-1\bigg)/\frac{150}{360}=3.79\%$$

Valuing Forward Rate Agreements

An existing FRA is valued by entering into an offsetting position at the new rate set on an FRA that expires at the same time as the original FRA. Thus,

• We are long the old FRA and thus will receive the rate \(L_{h}(m)\) at \(h\).
• We then go short a new FRA and agree to pay \(L_{h}(m)\) at \(h\) in order to value the FRA.

The value of an FRA is the present value of the difference between the new FRA rate and the old FRA rate:

$$V_{g}(0,h,m)=\frac{[FRA(g,h-g,m)-FRA(0,h,m)]t_{m}}{[1+D_{g}(h+m-g)t_{h+m-g}]}$$

To simplify the above equation, use the following steps to value ab FRA. 

• Calculate the new FRA rate at time g
• Compute the payoff at (h+m)

$$Payoff=(FRA_{g}-FRA_{0})\times\frac{m}{360}\times\text{Notional Amount}$$

• Discount back to time g

Example: Calculating the Value of an FRA

ABC Investment Bank entered into a \(6\times9\) FRA three months ago as the receive floating party. The following Exhibit gives the FRA data.

$$\small{\begin{array}{|l|c|}\hline\text{FRA Term} & 6\times9 \\ \hline\text{FRA rate} & 0.75\% \\ \hline\text{FRA notional amount} & \$300,000\\ \hline\end{array}}$$

The 90-day US Libor is 0.80%, and the 180-day Libor is 0.85%. At the time of expiration, the 3-month US dollar Libor is 1.00%, and the 6-month US dollar Libor is 1.10%. Assume that the applicable discount rate for the FRA settlement cashflows is 1%.

The value of the \(6\times9\) FRA three months after initiation using the 30/360 convention is closest to:

Solution

The value of an FRA is the present value of the difference between the new FRA rate and the old FRA rate:

$$V_{g}(0,h,m)=\frac{[FRA(g,h-g,m)]-FRA(0,h,m)]t_{m}}{[1+D_{g}(h+m-g)t_{h+m-g}]}$$

Note that \(6\times9\) FRA implies that the forward contract expires six months after initiation. Since the bank entered into the contract three months ago, this contract will expire in another three months.

The FRA value of receive floating can be determined using the following steps:

• Calculate the new FRA rate at time g

Here, we want to calculate \(FRA(g,h-g,m)\)

Formula:

$$FRA(g,h-g,m)=\frac{\bigg(\frac{[1+Lg(h-g+m)t_{h-g+m}]}{[1+L0(h-g)t_{h-g}]}-1\bigg)}{tm}$$

$$\begin{align*}FRA(90,90,90)&=\frac{\bigg(\frac{[1+L90(180)\times\frac{180}{360}]}{[1+\frac{L0(90)90}{360}]}-1\bigg)}{\frac{90}{360}}\\&=\bigg[\frac{1+0.0085\times\frac{180}{360}}{1+0.0080\times\frac{90}{360}}-1\bigg]\times\frac{360}{90}\\&=0.8982\%\end{align*}$$

• Compute the payoff at (h+m)

$$\text{Payoff}=(FRA_{g}-FRA_{0})\times\frac{m}{360}\times\text{Notional amount}$$

$$\begin{align*}\text{Payoff}&=(FRA_{90}-FRA_{0})\times\frac{90}{360}\times$300,000\\&=(0.8982\%-0.75\%)\times\frac{90}{360}\times$300,000\\&=$111.15\end{align*}$$

Discount back to time g, to determine \(V_{g}(0,h,m)\)

$$V_{0,h,m}=V_{90}(0,180,90)=\frac{$111.15}{1+\bigg(0.01\times\frac{180}{360}\bigg)}=$110.60$$

Currency Forward and Futures Contracts

Pricing Currency Forward Contracts

Foreign currency is quoted in units of the domestic currency.

The covered interest rate parity is the carry arbitrage model with foreign exchange. It is applied to determine the no-arbitrage forward price of a unit of foreign currency, in terms of the domestic currency, for a currency forward contract of length T (years):

$$F_{T}(\text{D\F})=S_{0}(D/{F})\bigg[\frac{(1+r_{D})^{T}}{(1+r_{F})^{T}}\bigg]$$

The above equation can also be expressed in the continuous form:

$$F_{T}(D/F)=S_{0}(D/{F})e^{(r_{D}-r_{F})^{T}}$$

Suppose the spot quote is in the base currency per unit of the quote/price currency. In that case, the base currency interest rate should be the numerator, and the quote currency interest rate should be the denominator.

For example, in the GBP/USD pair, GBP is the base currency and USD the quote currency.

Example: Calculating the price of a forward currency contract

The current spot exchange rate is $0.06757 per South African Rand (ZAR). Suppose that the risk-free rates are 4% in the United States and 6% in South Africa. The arbitrage-free forward exchange rate for a 90-day forward contract using assuming a 365 days year is closest to:

Formula:

$$F_{T}(\text{D\F})=S_{0}(D/{F})\bigg[\frac{(1+r_{D})^{T}}{(1+r_{F})^{T}}\bigg]$$

$$F_{T}(\text{USD\ZAR})=$0.06757\bigg[\frac{(1.04)^{\frac{90}{365}}}{(1.06)^{\frac{90}{365}}}\bigg]=$0.067$$

Valuing Currency Forward Contracts

After the initiation of the currency forward, its value can be determined using the formula:

$$V_{t}(T)=PV_{t,T}[F_{t}(T)-F_{0}(T)]$$

Note that the present value is computed using the price (Quote) currency interest rate.

Example: Calculating the value of a  currency Forward

An institutional forex trader bought A$500,000 against the USD at a price of \(F_{0}($/A$)=$0.76\) at time 0. Suppose that there are four months to expiration and the forward price is \(F_{t}($/A$)=$0.70\)

The USD interest rate is 1.5%, while the AUD interest rate is 1%.

The long position for this forward contract closest to:

Solution:

$$V_{t}(T)=PV_{t,T}(F_{t}(T)-F_{0}(T))$$

$$V_{t}(T)=\frac{$0.70-$0.76}{(1.015)^{\frac{4}{12}}}=-$0.0597 \text{per AUD}$$

Therefore, the long position is determined as:

$$=-\frac{$0.0597}{A$}\times\text{A}$1,000,000=-$59,702.97$$

Notice that the value of the forward position is negative to the trader, as the forward price of the Australian Dollar has decreased since the contract inception

Future Contracts

The general forward pricing and valuation equations, as seen in the previous sections, can be applied for both future and forward contracts:

Recall the two general formulas:

• Forward pricing: \(F_{0}(T)=FV_{0}, T(S_{0}+\theta_{0}-\gamma_{0})\)
• Forward valuation: \(V_{t}(T)=PV_{t,T}[F_{t}(T)-F_{0}(T)]\)

However, the future contract values differ from those of forward contracts as they are marked to market daily. This means that future values are zero at the end of each day as profits and losses are settled at the end of each day.

Question 1

An investor purchased a one-year Eurobond forward contract six months ago with a notional value of €50,000 at 100. Suppose that the current forward price for a contract with six months to maturity is 110, and the risk-free rate is 3%.

The value of the forward position is closest to:

1. €4,854.37
2. €4,926.50
3. €9,853.29

Solution

The correct answer is B:

The value of the forward position is the present value of the difference in forward prices.

$$V_{t}(T)=PV_{t,T}[F_{t}(T)-F_{0}(T)]$$

$$V_{t}(T)=(110-100)\times(1.03)^{-0.5}=\text{9.853 per €100 par}$$

Thus, \(\text{the position value}=0.09853\times€50,000=€4,926.50\)

Question 2

XYZ Inc. sold $50,000 against EUR forward at a forward rate of EUR 0.78 for $1 at Time 0. In the spot market at Time t, $1 is worth EUR 0.72, and the annually compounded risk-free rates are 2% for EUR and 5.00% for the USD. Assume at Time t the forward contract has three months to expiration. The forward price  at Time t will be closest to:

1. 0.7148
2. 0.7200
3. 0.7235

Solution

The correct answer is A:

$$F_{T}(\text{D\F})=S_{0}(\text{D}/\text{F})\bigg[\frac{(1+r_{D})^{T}}{(1+r_{F})^{T}}\bigg]$$

$$F_{T}(\text{EUR\USD})=S_{0}(USD)=S_{0}(USD)\bigg[\frac{(1+r_{EUR})^{T}}{(1+r_{USD})^{T}}\bigg]$$

$$F_{T}(\text{EUR\USD})=0.7200\bigg[\frac{(1.02)^{\frac{3}{12}}}{(1.05)^{\frac{3}{12}}}\bigg]=0.7148$$

Reading 37: Pricing and Valuation of Forward Commitments

LOS 37 (a): Describe and compare how equity, interest rate, fixed-income, and currency forward and futures contracts are priced and valued;

LOS 37 (b): Calculate and interpret the no-arbitrage value of equity, interest rate, fixed-income, and currency forward and futures contracts;