Interest Rate Forward and Futures Contracts

The most used interest rate in the derivatives market is the LIBOR which stands for London Interbank Offered Rate. LIBOR is the rate at which London banks can borrow from one another. When the loans are in dollars, they are referred to as Eurodollar time deposits, and the rate will be referred to as dollar LIBOR. Participants and lenders use the Libor to determine the interest payments on loans and derivatives payoffs.

The LIBOR will be phased out by the end of 2021 and replaced with a new market reference rate (MMR) such as SOFR and SONIA. Currently, there are active futures and forward markets for derivatives based on LIBOR. To understand the forward market, we need to look at the MRR spot market first. Let us use the following notations:

\(L_m\) = MRR spot rate (time=0) for any m-day deposit.

\(NA\) = Notional amount, the number of funds initially deposited.

\(NTD\) = Number of total days in a year used to calculate interest (360 in LIBOR market).

\(t_m\) = Accrual period.

\(TA\) = Terminal amount, the amount paid when LIBOR deposit is withdrawn.

In the forward market for LIBOR, a forward rate agreement is used. The forward rate agreement is an over-the-counter forward contract in which the underlying is an interest rate on a deposit. The forward rate agreement (FRA) has two counterparties:

1. The fixed-rate payer (long), also known as the floating receiver, pays interest on fixed rates and receives interest from floating rates. The fixed-rate payer profits from an MRR increase. A long FRA would suit a company looking to hedge against rising rates and is planning to borrow in the future.
2. The fixed-rate receiver (short), otherwise known as the floating rate payer, receives interest on fixed rates and pays interest on floating rates. The fixed-rate receiver profits from MRR decreases. A fixed-rate receiver is suitable for banks looking to have a fixed lending rate in the future.

To eliminate arbitrage opportunities, the FRA value is zero on the initiation date when there is no initial exchange of cash flows. FRAs are identified in the form of “X by Y,” where X and Y are the months. For example, a 4 by 10 indicates that in four months, the FRA will expire.

After the fourth month, the FRA payoff is based on the underlying rate, which is implied by the difference between 4 and 10, 6 months. Therefore, the payoff will be in 180 days MRR. If LIBOR is used, the rate will be computed based on the relationship between the spot rate on a four-month LIBOR deposit at the time of its initiation and the spot rate on a ten-month LIBOR deposit. A short FRA will use a four-month LIBOR deposit while a long FRA will use a ten-month LIBOR deposit. We assume that all months are 30 days long.

The difference between a floating interest payment and a fixed interest payment is settled in cash through the contract. The underlying of an FRA is just an interest payment. The counterparties to an FRA are not engaged in LIBOR deposit in the spot market. Rather, the spot market is used as a benchmark to determine FRA payoffs.

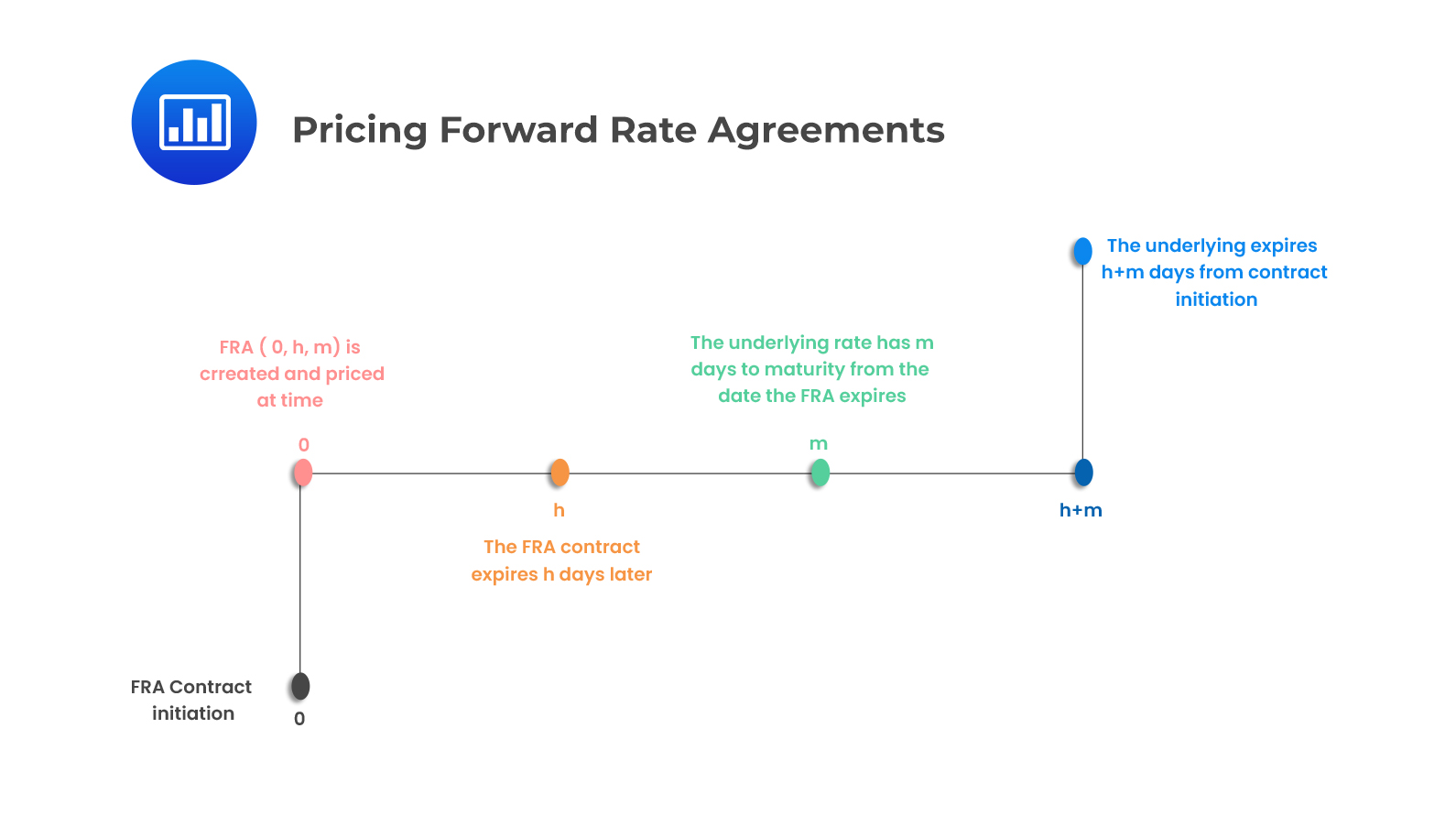Using the illustration above, we can describe key points in an FRA transaction. The FRA is priced on the initiation day at time 0 and it expires in time \(h\). The underlying has \(m\) days from FRA expiration before it matures at time \(T\). The FRA payoff is based on the spot m-day MRR observed in h days from the initiation of the FRA. Two spot rates: \(L_h\) and \(L_T\) are required to price the FRA. \(L_h\) makes use of the expiration of the FRA, while \(L_T\) makes use of the underlying maturity. The FRA hedges single period interest rate risk for the m-day period starting from h days in the future.

As MRR changes, our interest rate agreement’s value may either become positive or negative. Interest rate derivatives are settled in two ways at the expiration date:

1. Advanced Set, Settled in Arrears

This method is mainly used to settle swaps and interest rate options. The term advanced set refers to the interest rate that was set at the time money was deposited. The advanced set convention is always used because most market participants who have a position in a financial instrument would like to know a rate on the financial instrument. The term settled in arrears is used when an interest payment is made when the underlying instrument matures. For this reason, FRA with an advanced set settled in arrears works in a similar way a bank deposit works. The interest rate at time \(h\) is set at \(L_m\), and the interest is paid at time \(h + m\).

2. Advanced Set, Advanced Settled

FRAs are settled using this method. Advanced settled is used when the settlement is made at time \(h\). Note that in the advanced set the settlement is made when the FRA expires. Settlement amounts for the advanced set and advanced settled are discounted as follows:

Settlement amount at \(h\) for long (receive-floating):

$$NA ×\frac{[L_m-FRA_0 ] t_m}{[1+D_m t_m]}$$

The floating receiver loses when rates decrease. The floating rate \(L_m\) is received, and the \(FRA_0\) is paid.

Settlement amount at \(h\) for short (receive-fixed):

$$NA ×\frac{[FRA_0-L_m ] t_m}{[1+D_m t_m]}$$

The denominator,\(1+D_m t_m\), shows that the rate used to determine the payoff is derived from the spot market, which is settled in arrears. The discount factor is applied to the FRA payment because payment is advanced settled, but the loan’s interest is settled in arrears. It is assumed that at time \(h\), \(L_m\)=\(D_m\).

Example:

A company in the UK expects to deposit £2,000,000 in the next 30 days for 90 days. A 90-day LIBOR  is set 30 days from today. One of the company’s major concerns is that the interest rates could decrease. They have, therefore, been advised to negotiate a 1 by 4 FRA that expires in 30 days and is based on the 90-day LIBOR. The company agrees to enter a £2,000,000 notional amount 1 by 4 receive-fixed FRA that is advanced set and advanced settled. The discount rate for the FRA settlement cashflows is 3% and after 30 days, the 90-day LIBOR in pounds is 2.8%. Interest paid at maturity on the company’s deposit is most likely to be:

Solution

Since \(m\) is 90,

\(L_{90}= 2.8\%\)

$$ \text{ Settlement amount}=2,000,000 × [1+0.03(0.25)] = £ 2,014,000  $$

$$ \text{ Interest Paid}= £2,014,000 – £ 2,000,000  = £14,000$$              

The value of an FRA is the present value of the difference between the new FRA rate and the old FRA rate:

Long FRA value at time \(g\):

$$V_g=NA ×\frac{[FRA_g-FRA_0 ] t_m}{[1+D_{T-g} t_{T-g}]}$$

Short FRA value at time \(g\):

$$V_g=NA ×\frac{[FRA_0-FRA_g ] t_m}{[1+D_{T-g} t_{T-g}]}$$

Question

ABC Investment Bank entered into a \(6\times 9\) FRA three months ago as the receive floating party. The following Exhibit gives the FRA data.

$$ \textbf{FRA Data} \\ \begin{array}{c|c} \text{FRA term} & 6*9 \\ \hline \text{FRA rate} & 0.75\% \\ \hline \text{FRA notional amount} & $300,000 \\ \end{array} $$

The 90-day US LIBOR is 0.80%, and the 180-day LIBOR is 0.85%. At the time of expiration, the 3-month US dollar LIBOR is 1.00%, and the 6-month US dollar LIBOR is 1.10%. Assume that the applicable discount rate for the FRA settlement cashflows is 1%.

The value of the 6 × 9 FRA three months after initiation using the 30/360 convention is closest to:

1. $ 111.15.
2. $ 110.6.
3. $ 112.45.

Solution

The correct answer is B.

The value of an FRA is the present value of the difference between the new FRA rate and the old FRA rate:

$$ V_g\left(0,h,m\right)=\frac{\left\{\left[FRA_{\left(g,h-g,m\right)}-FRA_{\left(0,h,m\right)}\right]t_m\right\}}{\left[1+D_g\left(h+m-g\right)t_{h+m-g}\right]} $$

Note that \(6\times 9\) FRA implies that the forward contract expires six months after initiation. Since the bank entered the contract three months ago, this contract will expire in another three months.

The FRA value of receive floating can be determined using the following steps:

• Calculate the new FRA rate at time \(g\):

  Here, we want to calculate \(FRA_{\left(g,h-g,m\right)}\).

  Formula:

  $$ \begin{align*} FRA_{(g,h – g,m)} & = \frac { \left\{ \frac {\left[1 + L_g(h – g + m)t_{h–g+m}\right]}{ \left[ 1 + L_0(h – g)t_{h–g} \right]}– 1 \right\} } {{t_m}} \\ FRA_{\left(90,90,90\right)} &= \frac { \left\{ \frac {\left[1 + L_{90}(180)×\frac {180}{360} \right]}{\left[1 + \frac {L_0(90)90}{(360)} \right]}– 1 \right\} } { \frac {90}{360}} \\ & =\left[\frac{1+0.0085\times\frac{180}{360}}{1+0.0080\times\frac{90}{360}}-1\right]\times\frac{360}{90}=0.8982\% \end{align*} $$

• Compute the payoff at (\(h+m\)):

  $$ \begin{align*} \text{Payoff} &=\left(FRA_g-FRA_0\right)\times\frac{m}{360}\times \text{Notional amount} \\ \text{Payoff} &= \left(FRA_{90}-FRA_0\right)\times\frac{90}{360}\times$300,000 \\ & =\left(0.8982\%-0.75\%\right)\times\frac{90}{360}\times$300,000=$111.15 \end{align*} $$

Discount back to time \(g\), to determine \(V_g (0,h,m)\):

$$ V_g \left(0,h,m\right)=V_{90}\left(0,180,90\right)=\frac{$111.15}{1+\left(0.01\times\frac{180}{360}\right)}=$110.60 $$

Reading 33: Pricing and Valuation of Forward Commitments

LOS (c) Describe how interest rate forwards and futures are priced, and calculate and interpret their no-arbitrage value.