Single-Stage, Two-Stage, and Three-Stage FCFF and FCFE Models

Single-Stage (Constant-Growth) Free Cash Flow Models

FCFF Calculation

Assuming FCFF grows at a constant, \(g\), the next period’s FCFF will be:

$$\text{FCFF}_\text{t}=\text{FCFF}_{\text{t}-1} (1+\text{g})$$

If FCFF grows at a constant rate, the value of the firm is calculated as:

$$\text{Firm value}=\frac{\text{FCFF}_{1}}{\text{WACC}-\text{g}}=\frac{\text{FCFF}_0 (1+\text{g})}{\text{WACC}-\text{g}}$$

FCFE Calculation

Assuming FCFE grows at a constant rate, \(g\), the next period’s FCFE will be:

$$\text{FCFE}_\text{t}=\text{FCFE}_{\text{t}-1} (1+\text{g})$$

The value of equity is calculated as:

$$\text{Equity value}=\frac{\text{FCFE}_1}{\text{r}-\text{g}}=\frac{\text{FCFE}_0 (1+\text{g})}{\text{r}-\text{g}}$$

Where:

\(\text{r}=\) Required rate of return on equity.

\(\text{g}=\) Constant growth rate.

Two-stage Free Cash Flow Models

In a two-stage free cash flow model, the growth rate in the second stage is a long-term sustainable growth rate. For a declining industry, the second stage growth rate could be slightly lower than the economic growth rate or slightly higher for an industry experiencing strong growth.

There are two approaches to the two-stage FCFF and FCFE model differentiated by the growth rate in the first stage:

1. The growth rate is constant in stage 1 then abruptly drops to the long-term sustainable growth rate in stage 2.
   
2. The growth rate declines in stage 1 to reach the long-term sustainable rate at the beginning of stage 2. This is similar to the H-model in the dividend discounted model.
   

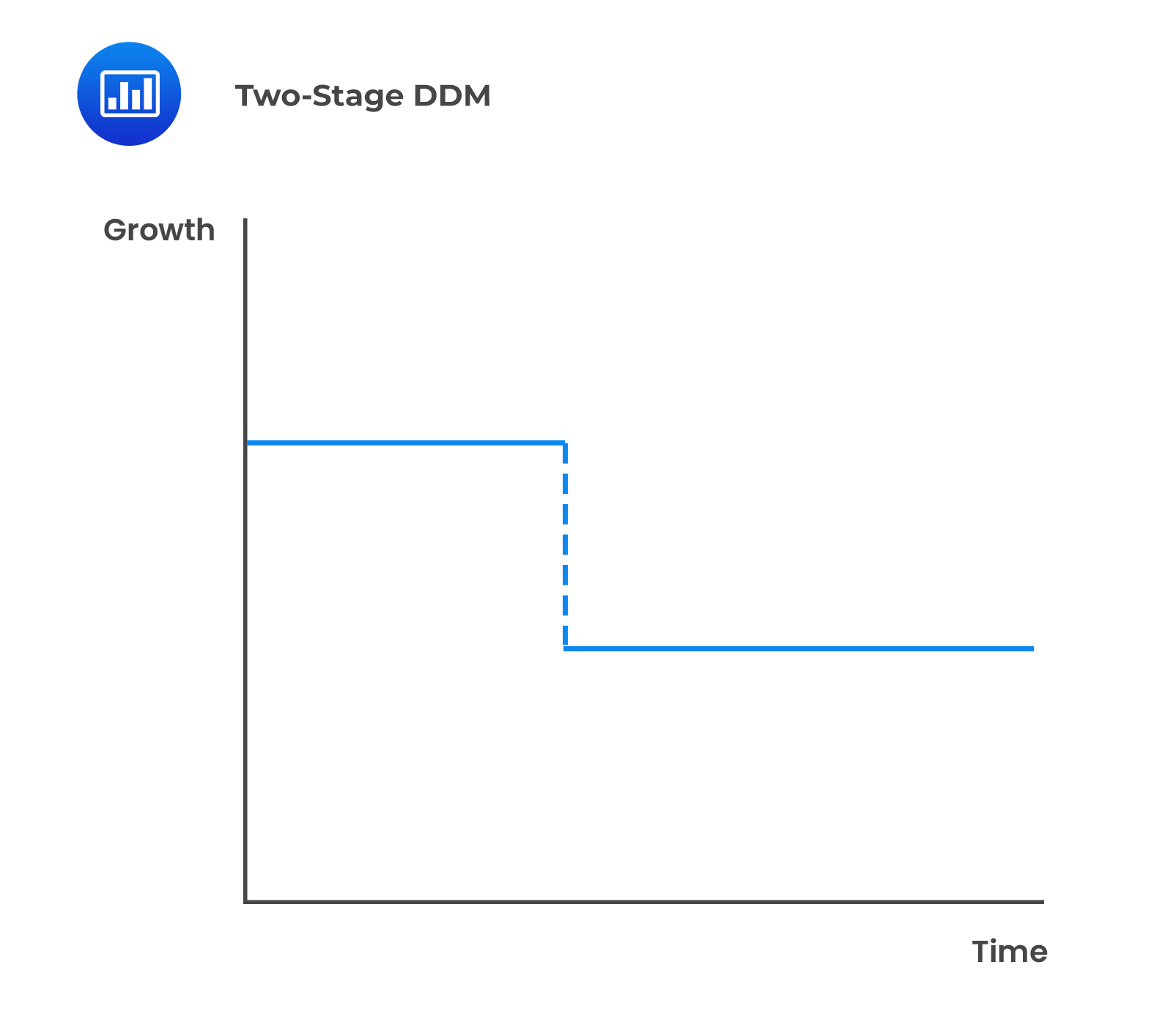
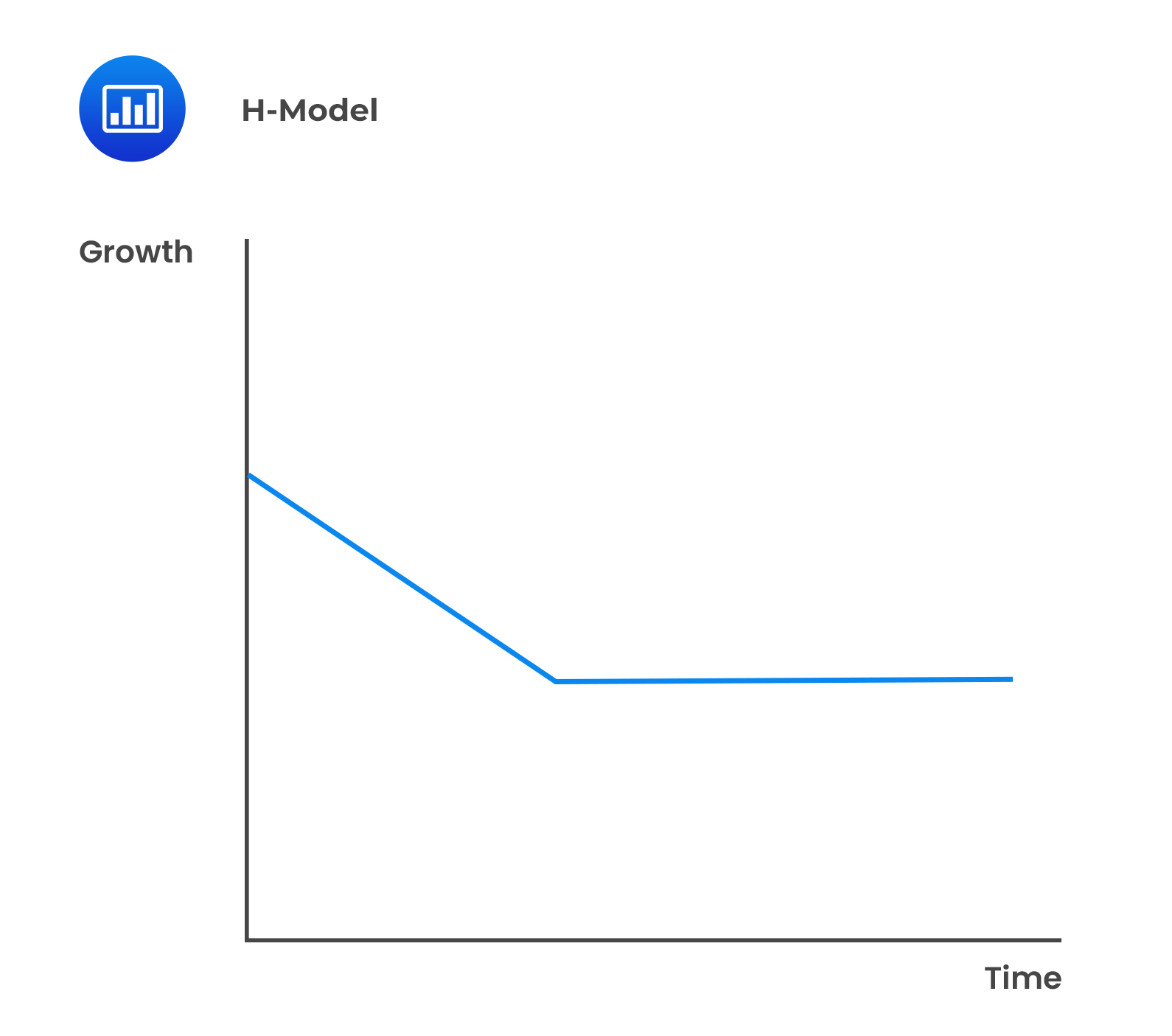
In free cash flow models, the growth rate may possibly refer to different variables, namely FCFF or FCFE, earnings (net income or operating income), or sales growth rates.

FCFF Calculation

The general two-stage FCFF valuation model is:

$$\text{Firm value}= ∑_{\text{t}=1}^\text{n}\frac{\text{FCFF}_\text{t}}{(1+\text{WACC})^\text{t}} +\frac{\text{FCFF}_{\text{n}+1}}{(\text{WACC}-\text{g})}\frac{1}{(1+\text{WACC})^\text{n}}$$

The terminal value is estimated by using a constant growth FCFF model, \(\frac{\text{FCFF}_{\text{n}+1}}{(\text{WACC}-\text{g})}\), which is discounted to the present by \(\frac{1}{(1+\text{WACC})^\text{n}}\).

Subtracting the value of outstanding debt from the firm value gives the value of equity. Finally, the value per share is estimated by dividing the total value of equity by the number of outstanding shares.

FCFF Calculation

The general two-stage FCFE valuation model is:

$$\text{Equity value}= ∑_{\text{t}=1}^\text{n}\frac{\text{FCFE}_\text{t}}{(1+\text{r})^\text{t}}+\frac{\text{FCFE}_{\text{n}+1}}{\text{r}-\text{g}} \frac{1}{(1+\text{r})^\text{n}}$$

The terminal value is estimated by using the constant growth FCFE model, \(\frac{\text{FCFE}_{\text{n}+1}}{\text{r}-\text{g}}\), which is discounted to the present by \(\frac{1}{(1+\text{r})^\text{n}}\).

The terminal value could also be estimated using the multiples approach. Here again, the value per share is calculated by dividing the total value of equity by the number of outstanding shares.

If a company has significant non-operating assets, such as excess cash and marketable securities, the company’s non-operating assets should be valued separately and then added to the value of the company’s operating assets to find total firm value.

$$\text{Value of the firm}=\text{Value of operating assets}+\text{Value of non-operating assets}$$

Three-Stage Growth Models

There are two approaches to this:

1. Assume a constant but different growth rate for the three stages.
   
2. Assume a constant growth rate in stages 1 and 3 and a declining growth rate in stage 2.
   

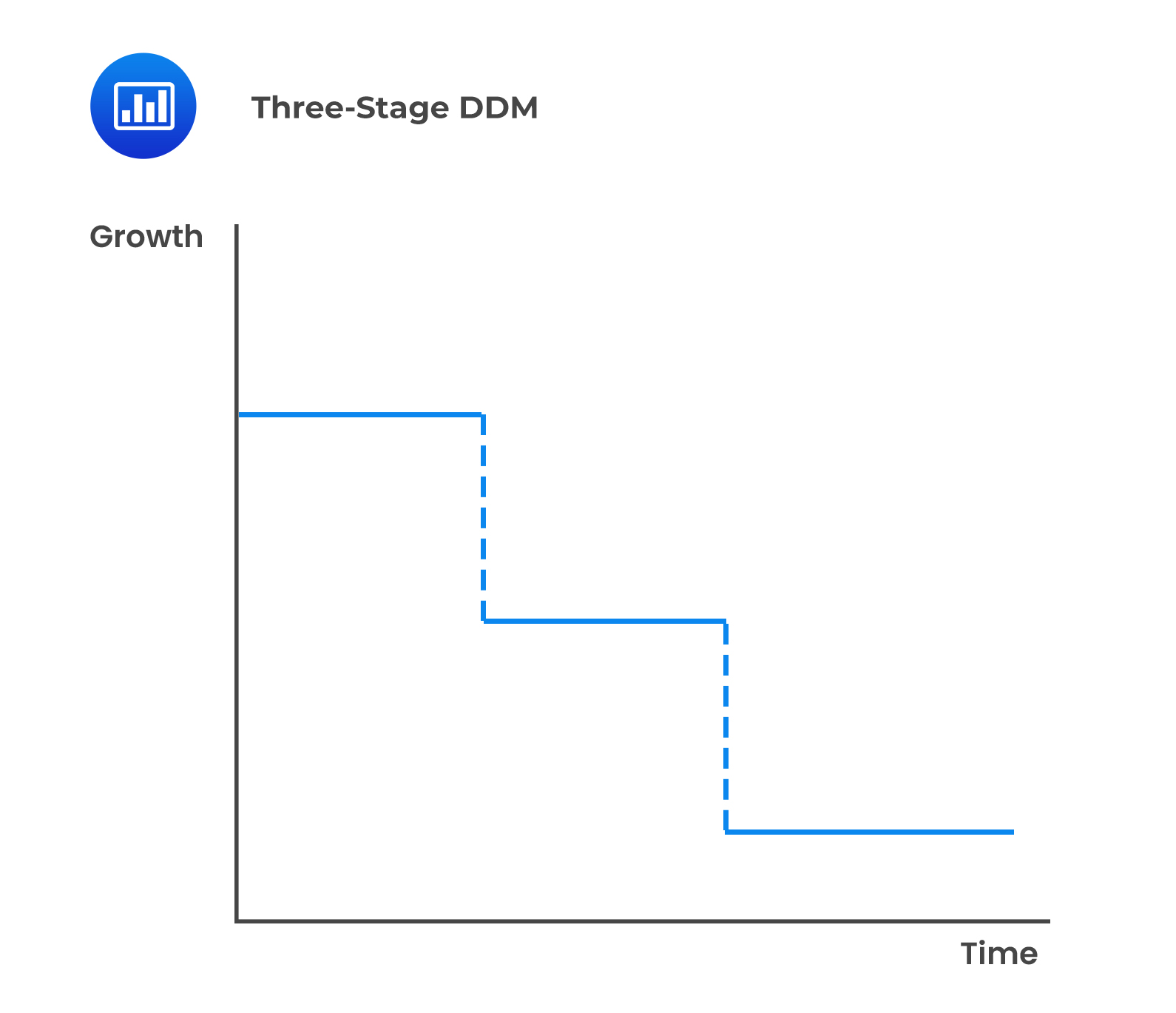
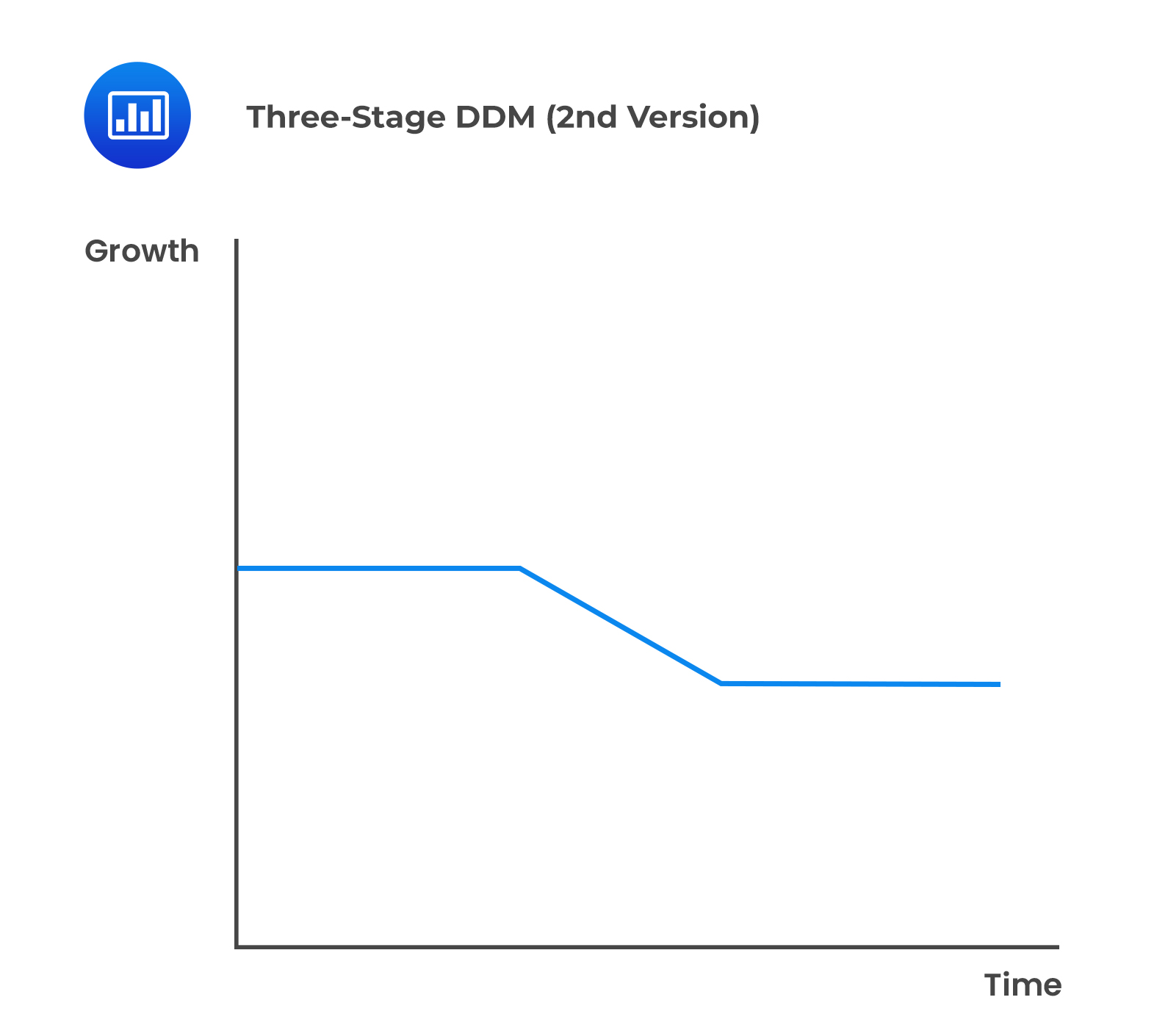
Question

Which of the following discount rates is applied to FCFF when computing the firm’s value?

1. WACC.
2. r−g.
3. r.

Solution

The correct answer is A.

The weighted average cost of capital (WACC) represents its blended cost of capital across all sources, including common shares, preferred shares, and debt. It is the rate that discounts the free cash flow to the firm (FCFF) to arrive at the value of the firm.

B is incorrect. r−g is used to discount FCFE.

C is incorrect. r is not used to discount FCFF.

Reading 24: Free Cash Flow Valuation

LOS 24 (i) Explain the single-stage (stable-growth), two-stage, and three-stage FCFF and FCFE models and select and justify the appropriate model given a company’s characteristics.