Valuing Embedded Options

According to the arbitrage-free framework, the value of a bond with embedded options is the sum of the arbitrage-free value of the option-free bond (straight bond) and the arbitrage-free values of any embedded options.

Embedded Calls

A callable bond is similar to a portfolio with a long position on a straight bond and a short position on a call option. The issuer makes the decision to exercise the call option.

$$ \begin{align*} \text{Value of callable bond}& =\text{Value of straight bond} \\ & –\text{Value of issuer call option} \\ \text{Value of issuer call option}& =\text{Value of straight bond} \\ & – \text{Value of callable bond} \\ \end{align*} $$

i.e.,

$$ \begin{align*} V_{\text{Callable}} &= V_{\text{Straight}} – V_{\text{Call}} \\ V_{\text{Call}} &= V_{\text{Straight}} – V_{\text{Callable}} \end{align*} $$

This has been illustrated in the following diagram:

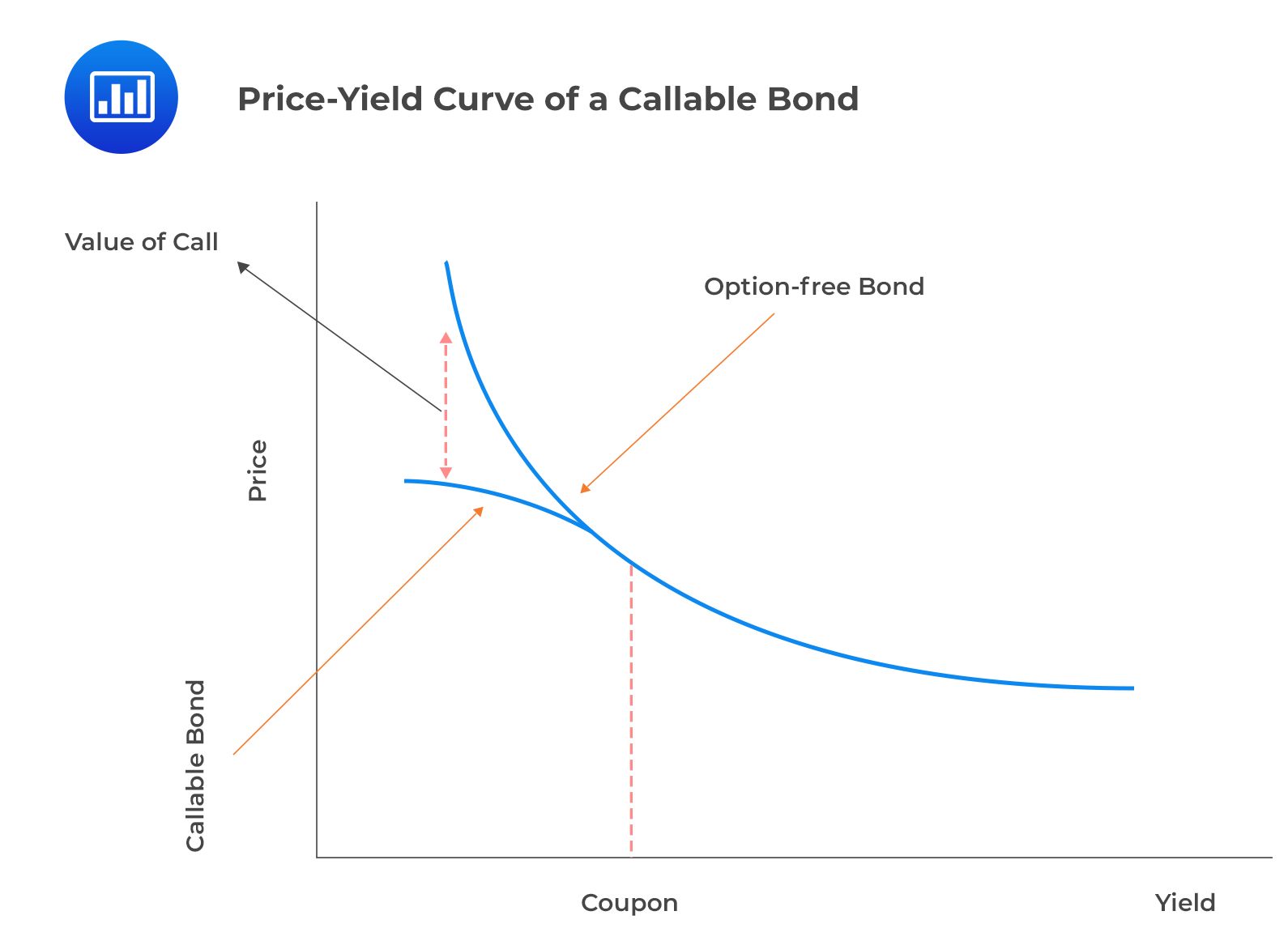It is worth noting that callable bonds are riskier, have higher spreads, and generate higher yields relative to put bonds.

Embedded Puts

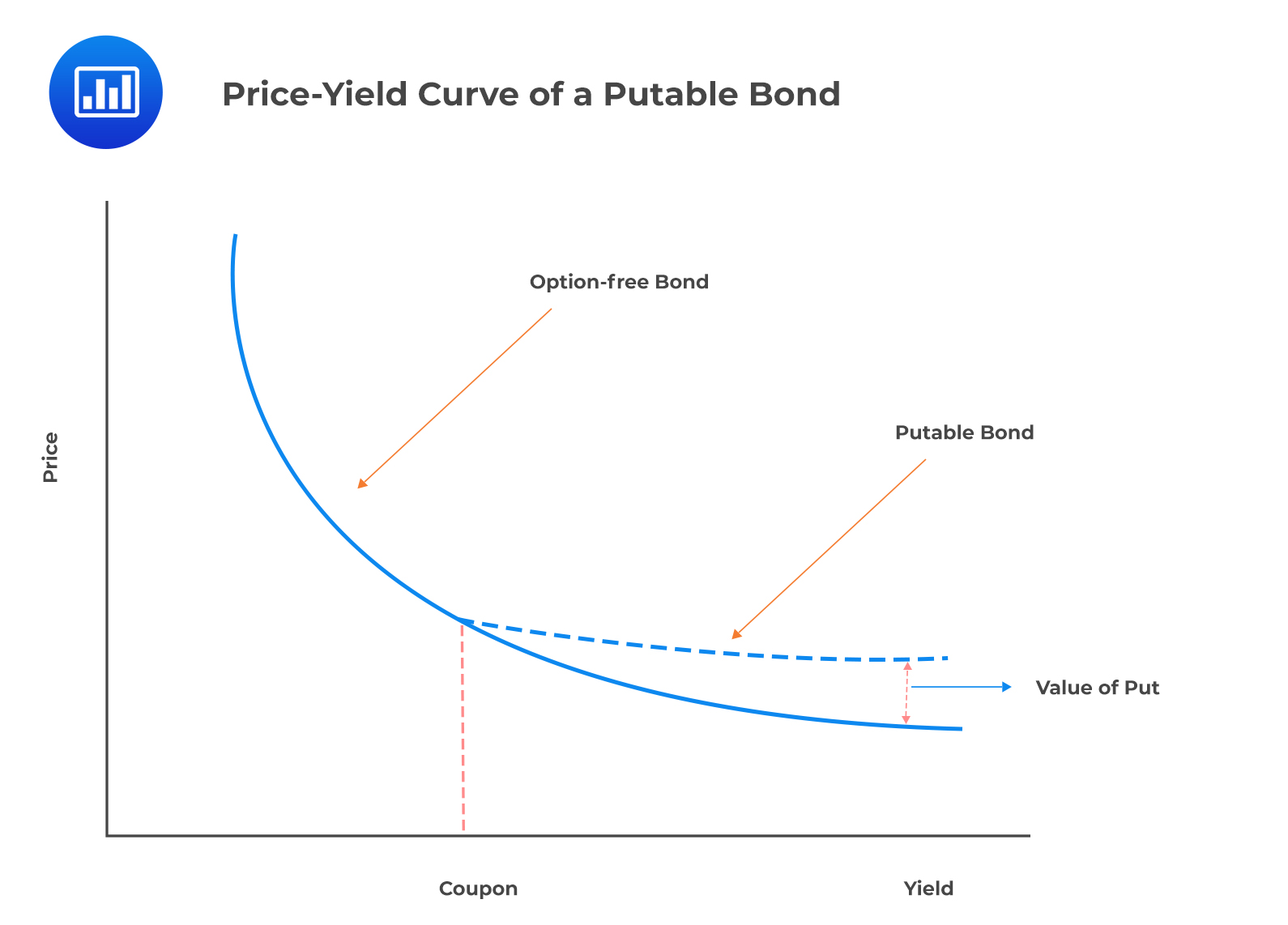
The investor has a long position in both the straight bond and the put option.

$$ \begin{align*} \text{Value of putable bond} & =\text{Value of straight bond} \\ & +\text{Value of investor put option} \\ \text{Value of investor put option} & =\text{Value of putable bond} \\ & – \text{Value of straight bond} \end{align*} $$

i.e.,

$$ \begin{align*} V_{\text{Putable}}= V_{\text{Straight}}+ V_{\text{Put}} \\ V_{\text{Put}}=V_{\text{Putable}} – V_{\text{Straight}} \end{align*} $$

The concept of embedded puts is illustrated in the following diagram:

Question

The value of an option free, 5% annual coupon bond that matures in three years is $106.80. If the value of a callable bond with similar terms is $105.50, the value of the issuer call option is closest to:

1. -$1.30.
2. $0.00.
3. $1.30.

Solution

The correct answer is C.

$$ \begin{align*} \text{Value of issuer call option} &=\text{Value of straight bond} \\ & – \text{Value of callable bond} \\ V_{\text{Callable}} &=$105.50 \\ V_{\text{Straight}} &=$106.80 \\ V_{\text{Call}} &=$106.80-$105.50=$1.30 \end{align*} $$

Reading 30: Valuation and Analysis of Bonds with Embedded Options

LOS 30 (b) Explain the relationships between the values of a callable or putable bond, the underlying option free (straight) bond, and the embedded option.