Relevant Adjustments for Improving Qua ...
Off-Balance-Sheet Financing Off-balance-sheet financing is an accounting practice where companies exclude liabilities on... Read More
Recall from the first learning objective of this reading that the forward rate lies above the spot rate for an upward sloping spot curve. On the other hand, the forward rate in a downward sloping spot curve lies below the spot rate.
This relationship in a downward sloping spot curve is shown in the figure below:
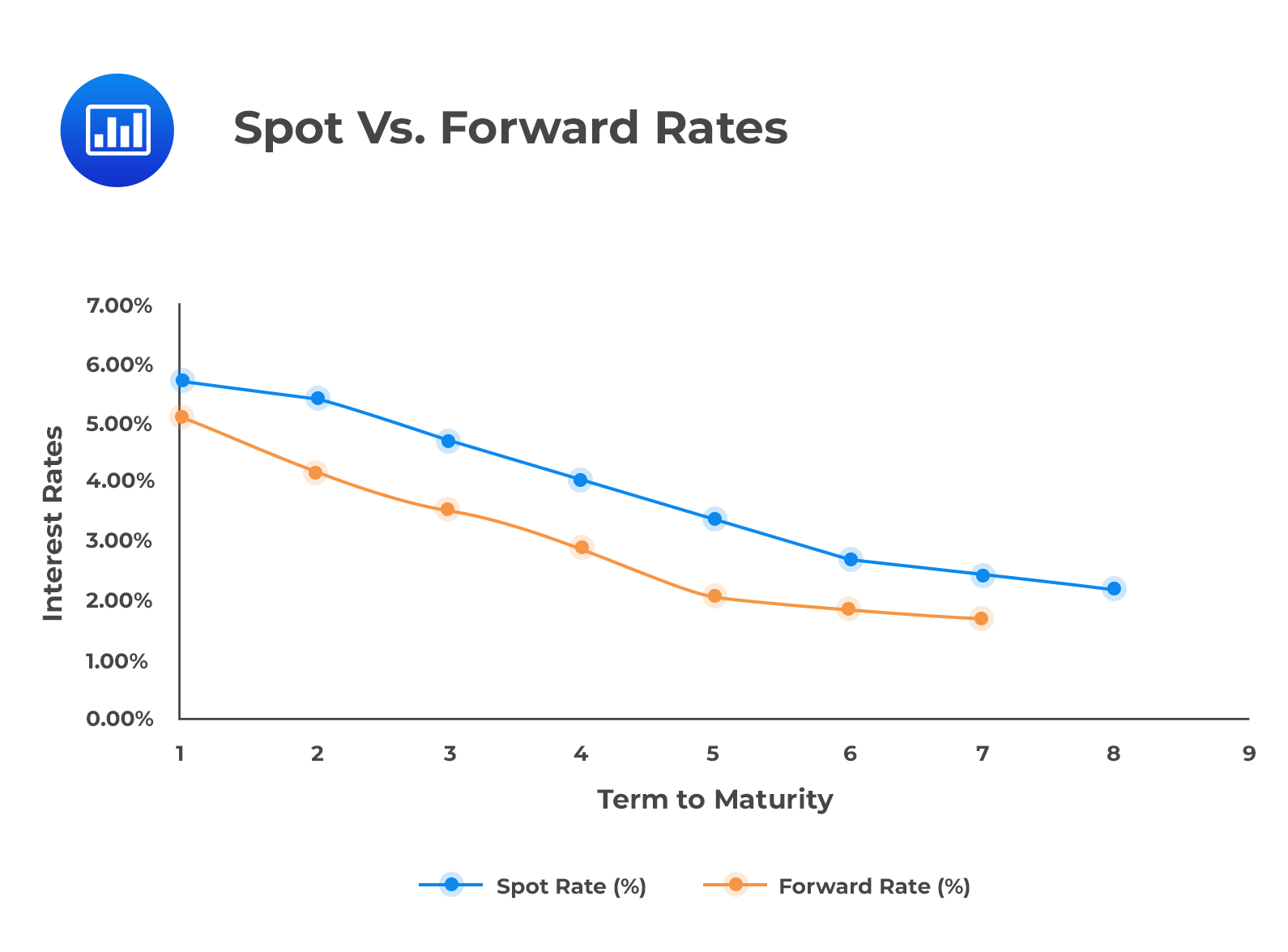 The Spot Rate for Long-Maturity Securities
The Spot Rate for Long-Maturity SecuritiesThe spot rate for a bond with a maturity greater than 1 is equal to the geometric mean of the one-period spot rate and a series of one-year forward rates.
From the forward rate model:
$$ \left(1+S_T\right)^T=(1+S_1)\left[1+f\left(1,T-1\right)\right]^{T-1} $$
Which can be expanded to:
If \(t=1\),
$$ \begin{align*} & \left(1+S_T\right)^T \\ & =(1+S_1)(1+f(1,1)(1+f(2,1)(1+f\left(3,1\right)\ldots (1+f\left(T-1,1\right)\ldots({1}) \\ & S_T \\ & =[(1+S_1)(1+f(1,1)(1+f(2,1)(1+f\left(3,1\right)\ldots \\ & \left(1+f\left(T-1,1\right)\right]^\frac{1}{T}-1\ldots({2}) \end{align*} $$
Contrary to the unbiased expectations theory, active bond portfolio management suggests that forward rates are biased predictors of future spot rates. In other words, the forward curve does not accurately forecast future spot rates.
Thus, an active portfolio manager tries to outperform the bond market by forecasting how the future spot rates will differ from those reflected by the current forward curve.
The following information relates to three zero-coupon bonds.
$$ \begin{array}{c|c} \textbf{Maturity} & \textbf{Spot Rates} \\ \hline 1 & 10\% \\ \hline 2 & 11\% \\ \hline 3 & 12\% \end{array} $$
Solution
$$ \begin{align*} (1+f\left(1,1\right)) &=\frac{\left(1+S_2\right)^2}{\left(1+S_1\right)} \\ f\left(1,1\right) & =\frac{{1.11}^2}{1.10}-1=1.1201-1=12.01\% \end{align*} $$
$$ \begin{align*} (1+f\left(2,1)\right) &=\frac{\left(1+S_3\right)^3}{\left(1+S_2\right)^2} \\ f\left(1,2\right) & =\frac{{1.12}^3}{{1.11}^2}-1=14.03\% \end{align*} $$
$$ \begin{align*} \left(1+S_2\right)^2 & =(1+S_1)(1+f(1,1)) \\ S_2 & =\left[\left(1+0.10\right)\left(1+0.1201\right)\right]^\frac{1}{2}-1\approx11\% \\ \left(1+S_3\right)^3 & =[\left(1+S_1\right)(1+f(1,1)(1+f\left(2,1\right)] \\ S_3 &=\left[\left(1.10\right)\left(1.1201\right)\left(1.1403\right)\right]^{\left(\frac{1}{3}\right)}-1 \\ & =\approx12\% \end{align*} $$
Question
A bond whose expected spot rate is lower than the current forward rate is most likely:
- Undervalued.
- Overvalued.
- Fairly valued.
Solution
The correct answer is A.
The bond’s expected price determined using a lower expected discount rate (spot rate) is higher than the price obtained using the current forward rate discount factor. This implies that the bond will be undervalued.
Reading 28: The Term Structure and Interest Rate Dynamics
LOS 28(c) Describe the assumptions concerning the evolution of spot rates in relation to forward rates implicit in active bond portfolio management.