Value of a Bond and its Credit Spread

The arbitrage-free framework is applied for credit analysis of a risky bond, assuming that interest rates are volatile. A binomial interest rate tree is constructed assuming no arbitrage. The tree is then verified if it has been correctly calibrated and used to value corporate bonds.

Fixed Coupon Corporate Bonds

A fixed coupon corporate bond can be evaluated using the binomial interest rate tree in the following steps:

• Calculate the value of the bond assuming no default (VND).
• Determine the credit valuation adjustment (CVA).
• Work out the bond’s fair value, where fair value = VND – CVA.
• Determine the yield to maturity (YTM) of the bond using fair value.
• Calculate the credit spread of the bond using YTM.
• Work out the credit spread, where credit spread = YTM of the risky bond – Benchmark YTM.

Example 1: Zero-volatility Benchmark Rates

Consider a four-year zero-coupon corporate bond with a par value of $1,000 and a flat government bond yield curve at 5%. The risk-neutral probability of default (hazard rate) for each date of the bond is 2%, and the recovery rate is 40%.

1. The fair value bond is closest to:
2. The YTM of the bond is closest to:
3. The credit spread of the bond is closest to:

Solution

1. Fair value

   $$ \begin{align*} \text{Value of the bond assuming no default (VND)} &= \frac{1000}{\left(1+0.05\right)^4} \\ & = 822.70 \end{align*} $$

   Recall the calculation of CVA from a previous LOS.

   $$ \begin{array}{c|c|c|c|c|c|c|c} \textbf{Year} & \textbf{EE} & \textbf{LGD} & \textbf{Hazard } & \textbf{PD} & \textbf{PS} & \textbf{EL} & \textbf{PV} \\ & & & \textbf{rate} & & & & \textbf{of} \\ & & & {} & & & & \textbf{EL} \\ \hline 1 & 863.84 & 518.30 & 2\% & 2.0000\% & 98.000\% & 10.37 & 9.8724 \\ \hline 2 & 907.03 & 544.22 & 2\% & 1.9600\% & 96.040\% & 10.67 & 9.6750 \\ \hline 3 & 952.38 & 571.43 & 2\% & 1.9208\% & 94.119\% & 10.98 & 9.4815 \\ \hline 4 & 1,000.00 & 600.00 & 2\% & 1.8824\% & 92.237\% & 11.29 & 9.2919 \\ \hline & & & & & & \textbf{CVA} & \bf{38.321} \end{array} $$

   • EE = Expected exposure
   • LGD = Loss given default
   • PD = Probability of default
   • PS = Probability of survival
   • EL = Expected loss

   $$ \begin{align*} \text{Fair value} & =\text{VND} -\text{CVA} \\  & = 822.70 – 38.32 =$784.38 \end{align*} $$

2. YTM

   YTM of the bond can be determined as the rate that solves the equation:

   $$ \begin{align*} 784.38 & =\frac{1000}{\left(1+\text{YTM}\right)^4} \ \text{YTM} & = 6.26\% \end{align*} $$

3. Credit spread

   $$ \begin{align*} \text{Credit spread} & = \text{YTM of the risky bond}\ – \text{Benchmark YTM} \\  & = 6.26\% – 5\% = 1.26\% \end{align*} $$

   Thus, the compensation for credit risk received by the investor can be expressed in terms of:

   • The CVA, 38.32, which is the present value per 100 of par value on today.
   • A credit spread of 126 basis points, which is an annual percentage rate for four years.  

Example 2: Volatility Assumption

In the previous example, we have determined the fair value and the credit spread of a risky bond, assuming a flat benchmark yield curve. This example will use the binomial interest rate tree to calculate the value of the bond assuming no default (VND) and the expected exposure in a volatile interest rate environment.

Given the spot rate curve for the annual payment benchmark Treasury, we can derive the discount factors and forward rates as per the following table:

$$ \begin{array}{c|c|c|c} \textbf{Maturity} & \textbf{Spot Rates} & \textbf{Discount Factors (DF)} & \textbf{Forward Rates} \\ \hline 1 & 4.00\% & 0.96154 & 4.000\% \\ \hline 2 & 5.00\% & 0.90703 & 6.010\% \\ \hline 3 & 6.00\% & 0.83962 & 8.029\% \end{array} $$

Using the above forward rates, an iterative process has been used to generate the following binomial tree, assuming an interest rate volatility of 15%.

$$ \begin{array}{ccc} \textbf{Time 0} & \textbf{Time 1} & \textbf{Time 2} \\   & & 10.69\% \\  & 6.89\% & \\   4.000\% & & 7.86\% \\   & 5.12\% & \\   & & 5.90\% \end{array} $$

Consider a 5%, three-year corporate bond with a par value of $1,000. The risk-neutral probability of default for this bond has been estimated as 2%, and the recovery rate as 40%

We can determine the fair value of the bond as follows:

The first step is to determine the value of the bond, assuming no default (VND). This is done through backward induction.

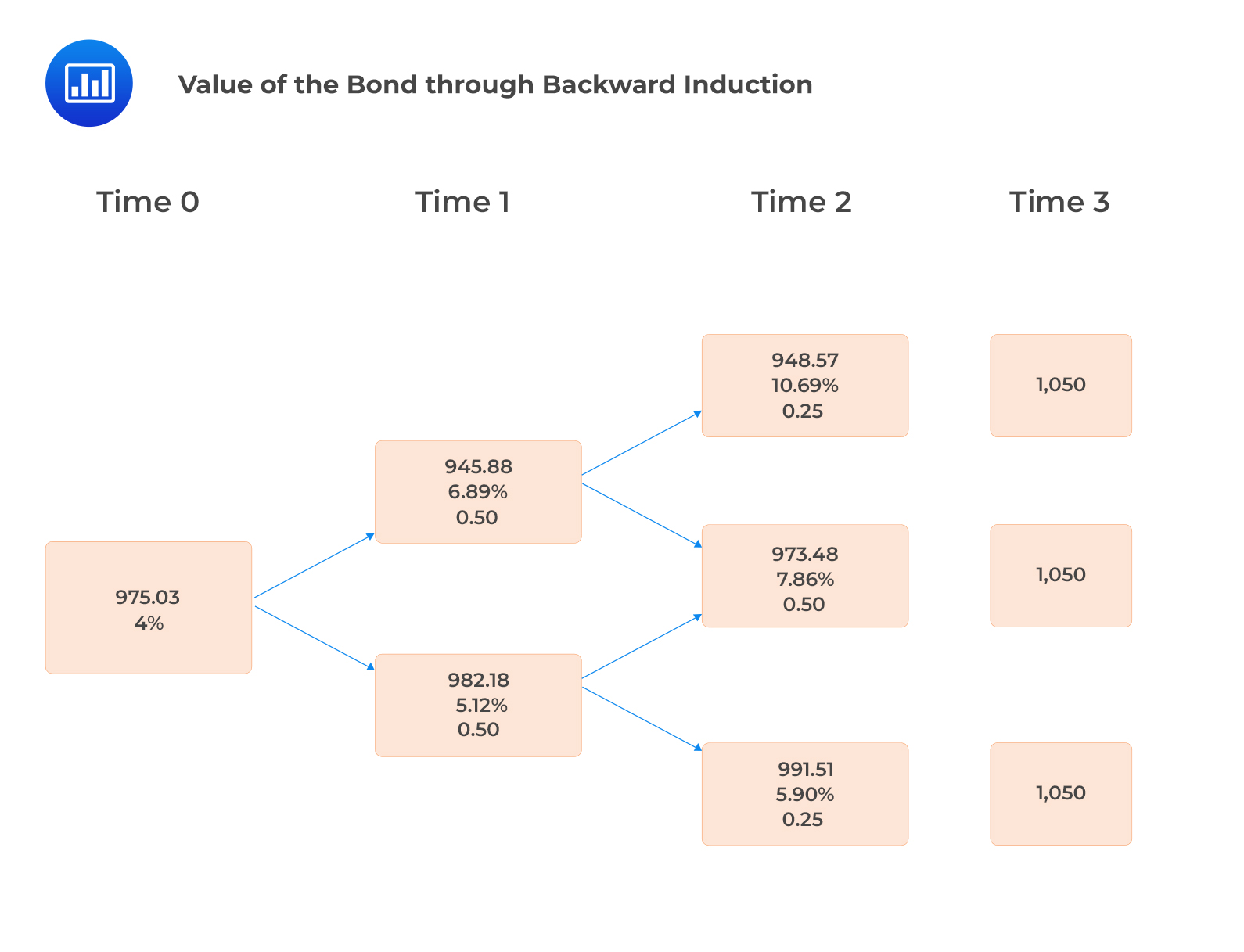N/B: The values in the above tree are subject to rounding errors

Year 3 cashflows are the principal (1,000) plus the coupon of 50.

Year 2 values for the bond are obtained as follows:

$$ \begin{align*} \frac{1050}{1.1069} &=948.59 \\ \\ \frac{1050}{1.0786} &=973.48 \\ \frac{1050}{1.0590} & =991.50 \end{align*} $$

Year 1 values are obtained as follows:

$$ \begin{align*} \frac{1}{2}\times\frac{\left(948.59+50\right)+\left(973.48+50\right)}{1.0689} & =945.86 \\ \\ \frac{1}{2}\times\frac{\left(973.48+50\right)+\left(991.50+50\right)}{1.0512} &= 982.20 \end{align*} $$

Year 0 Value (VND) are obtained as follows:

$$ \frac{1}{2}\times\frac{\left(945.86+50\right)+\left(982.20+50\right)}{1.04}=975.03 $$

VND can also be determined by discounting the bond’s yearly cashflows at the relevant spot rates:

$$ VND =\frac{50}{1.04}+\frac{50}{\left(1.05\right)^2}+\frac{1,050}{\left(1.06\right)^3}=$975.03 $$

However, the binomial tree is key for calculating the expected exposure at each node when computing the CVA.

$$ \begin{align*} & \text{Expected exposure at each year} \\ & =\sum{\text{Value in node i at time t}\times \text{Probability}}+\text{Coupon for year t} \end{align*} $$

The next step is to calculate CVA.

$$ \begin{array}{c|c|c|c|c|c|c|c} \textbf{Year} & \textbf{EE} & \textbf{LGD} & \textbf{PD} & \textbf{PS} & \textbf{EL} & \textbf{Discount} & \textbf{PV of} \\ & & & & & & \textbf{Factors} & \textbf{EL} \\ \hline 1 & 1,014.03 & 608.42 & 2.000\% & 98.00\% & 12.17 & 0.9615 & 11.70 \\ \hline 2 & 1,021.76 & 613.05 & 1.960\% & 96.04\% & 12.02 & 0.9070 & 10.90 \\ \hline 3 & 1,050.00 & 630.00 & 1.921\% & 94.12\% & 12.10 & 0.8396 & 10.16 \\ \hline & & & & & & \textbf{CVA} & \bf{32.76} \end{array} $$

$$ \begin{align*} & {\text{Expected exposure for each year}} \\ & = \sum{\text{(Value at each node }}\times {\text{Probability}}) +{\text{Coupon}} \end{align*} $$

$$ \begin{align*} \text{Expected exposure for year one} & =\left(945.88\times0.5\right)+\left( 982.18\times0.50\right) \\ & +50 \\ & =1,014.03 \\ \text{Expected exposure for year two} & = (948.57\times0.25)+\left( 973.48\times0.5\right)\\ & +\left(991.51\times0.25\right) +50 \\ & =1,021.76 \\ \text{Expected exposure for year three} & = 1,050 \end{align*} $$

$$ \begin{align*} \text{Loss given default (LGD)} & = \left(1-\text{Recovery rate}\right)\times \text{Expected exposure} \\ LGD_1 & = 1,014.03\times\left(1-0.40\right)=608.42 \\ LGD_2 &= 1,021.76\times\left(1-0.40\right)=613.05 \\ LGD_3 &=1,050\times\left(1-0.40\right)=630.00 \end{align*} $$

The probability of default is calculated using the formula:

$$ PD_t=PS_{t-1}\times \text{Hazard rate} $$

Where:

$$ \begin{align*} \text{Probability of survival } (PS_t) &= 1- {\text{Cumulative conditional} \\ \text{probability of default}} \\ \text{Expected loss} & = LGD\times PD \\ \text{PV of expected loss} &=LGD\times\frac{PD}{\left(1+i\right)^t} \\ \end{align*} $$

CVA = sum of the present value of the expected loss for each period.

CVA = $32.76

VND = $975.03

$$ \begin{align*} \text{The fair value of the bond} & = VND\ – CVA \\ \text{Fair value}&= 975.03-32.76=$942.27 \end{align*} $$

Note that changes in the interest rate volatility have minimal effect on a corporate bond’s fair value. The volatility assumption has more weight on bonds with embedded options.

Similar to a fixed-coupon corporate bond, the arbitrage-free framework can also be used to analyze a floater as follows:

1. Determine the VND given the quoted margin
2. Calculate the CVA
3. Fair value = VND – CVA
4. Determine the discount margin by trial and error.

Question

A $1,000 par, 6% annual coupon corporate bond matures five years from today. The bond is currently priced with a credit spread of 150 bps over the benchmark par rate of 3%. The bond’s CVA is closest to:

1. $43.63.
2. $60.00.
3. $1,084.86.

Solution

The correct answer is A.

$$ CVA = VND- \text{Price of risky bond} $$

VND is the value of the cash flows arising from the bond, discounted at the benchmark par rate

In this case,

$$ VND=\frac{60}{1.03}+\frac{60}{{1.03}^2}+\frac{1060}{{1.03}^3}=$1,084.86 $$

Price of the risky bond using credit spread = 3% benchmark rate + 1.5% = 4.5%. We will therefore discount the bond’s cash flows assuming a YTM of 4.5%

$$ \begin{align*} \text{Price of risky bond} &=\frac{60}{1.045}+\frac{60}{{1.045}^2}+\frac{1060}{{1.045}^3}=$1,041.23 \\ CVA &=$1,084.86-$1,041.23=$43.63 \end{align*} $$

Reading 31: Credit Analysis Models

LOS 31 (e) Calculate the value of a bond and its credit spread, given assumptions about the credit risk parameters.