Using Options to Hedge a Short Position

Options strategies are, by nature, highly flexible and customizable. They can be combined based on market expectations, attitudes, desires, and existing portfolio setups. While the strategies and combinations discussed have common goals, objectives, and setups, it’s important to remember that the actual characteristics of a position are revealed by the Greeks, not solely by the strategy’s name.

Combining Long Calls and Short Stock

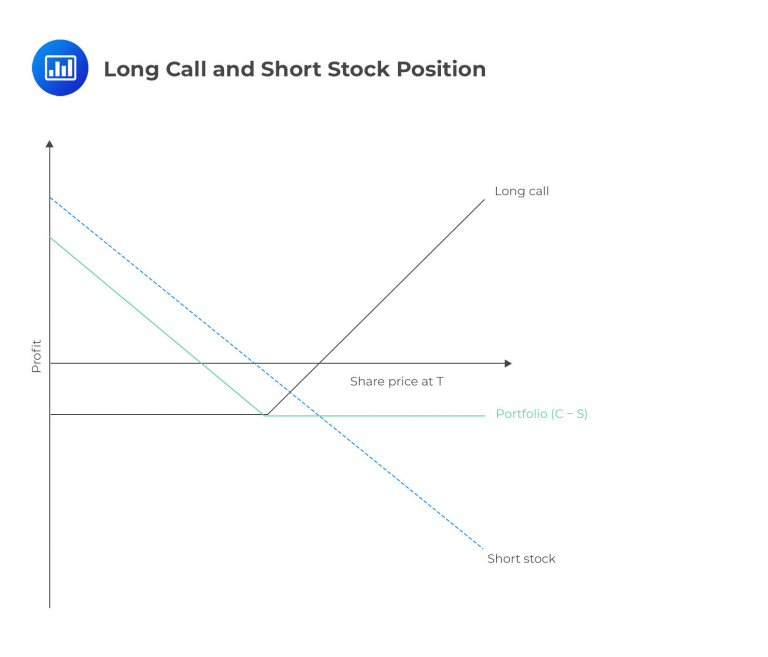
Combining long calls and short stock involves borrowing and selling stock while simultaneously holding a long call option. The long call aims to protect against upward price movements in the shares. As the short stock position loses value when the underlying stock price increases, the long call helps limit the potential cost of buying back the shares and closing the position (capped at the call strike price).

This position can loosely be considered the opposite or inverse of a married put position, although the mathematical equivalence may not be accurate. Nevertheless, the sentiment and objectives of this strategy align with those of a long stock and long put position.

$$ \text{Total position value} = \text{Value of the short stock}+\text{Value of the long call} $$

Where:

• Value of the short stock \(= (S_0 – S_T)\).
• Value of the long call \(= \text{max } (0, S_T–K)\).
• Total position value \(= (S_0 – S_T) + \text{max } (0, S_T – K)\).

and

\(S_0\)= Initial short price (sale price).

\(S_T\) = Ending stock price.

\(K\) = Strike price.

It is important to remember that the formula provided above needs to be adjusted to incorporate the premium paid for the long call option. Including the call premium will reduce potential gains and amplify potential losses. The formula’s negative relationship between \(-S_T\) and \(+S_T\) highlights the hedging nature of these positions. Investors often use this strategy to hedge their short stock position. They can secure their profits by purchasing a put option while potentially allowing the position to move favorably. The diagram below illustrates the combination of a long call and a short stock position.

Combining Short Puts and Short Stock

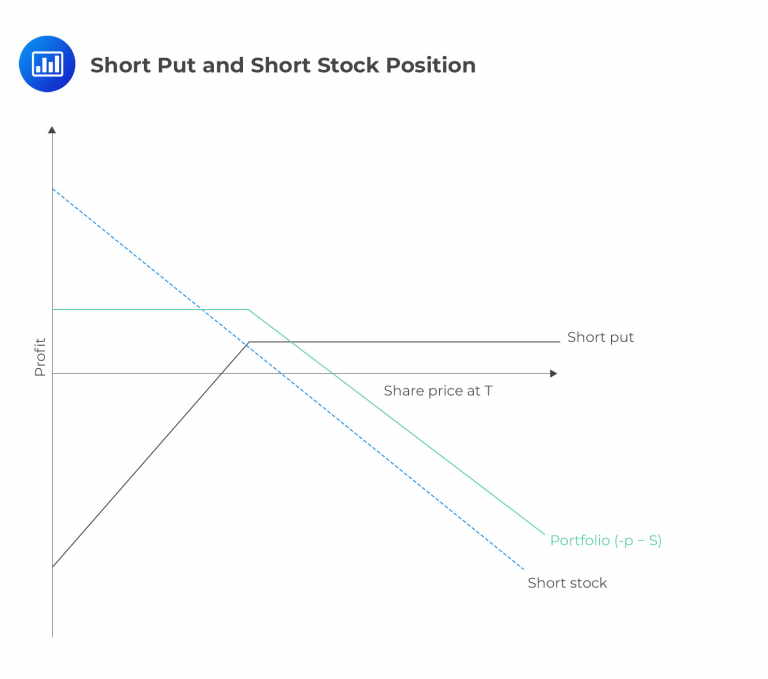
In this strategy, an investor sells short stock and puts options. By shorting the stock, the investor anticipates a decline in its price, while selling the put options allows them to earn a premium with the hope that the options will expire worthless. However, it’s important to note that if the stock price decreases, the investor who sold the puts may be obligated to buy back the stock at the strike price. This can offset the gains from the short stock position if the stock continues to decline. While there are some similarities to a covered call strategy, where a call option is sold against a long stock position, the dynamics and risk profiles differ. It’s essential to consider this strategy’s potential risks and rewards carefully.

Total position value

$$ \text{Total position value} = (S_0-S_T)-\text{Max}(0,K-S_T) $$

Where:

\(S_0\) = Initial short price (sale price).

\(S_T\) = Ending stock price.

\(K\) = Strike price.

The following figure shows a short put and short stock combination.

Question

An investor with a position short 100 shares of MKST would most likely choose to short puts against the position to?

1. Decrease overall position delta.
2. Reduce Beta.
3. Generate income.

Solution

The correct answer is C.

Generating income is one of the benefits of writing options, whether they are puts or calls. Investors who take on the potential obligation to transact in the future receive compensation for assuming that risk.

A is incorrect. Shorting stock results in negative delta exposure. Since buying a put option also creates negative delta exposure, it follows that selling (writing/shorting) puts would result in positive delta exposure. Therefore, the answer to the question is not decreasing the overall delta.

B is incorrect. Market beta risk, measured by beta, is a concept that relates to overall systemic risk in the market rather than the specific risk associated with a single security as measured by delta. Therefore, reducing beta is not the purpose or result of shorting puts in this context.

Derivatives and Risk Management: Learning Module 1: Options Strategies; Los 1(e) Compare the effect of buying a call on a short underlying position with the effect of selling a put on a short underlying position