Probability Rules

Probability rules are the concepts and facts that must be taken into account while evaluating the probabilities of various events. The CFA curriculum requires candidates to master 3 main rules of probability. These are the multiplication rule, the addition rule, and the law of total probability. We now look at each rule in detail.

Multiplication Rule

We use the multiplication rule to determine the joint probability of two events, P (AB). A joint probability is the probability of two events happening together. For example, we may be interested in the probability that gas prices and bus fares increase concurrently.

Note: If two events are mutually exclusive, then they cannot occur together. Therefore, we say that such events have zero joint probability.

The multiplication rule states that:

$$ P(AB) = P(A | B)P(B) $$

Example: Multiplication rule

Let’s assume we have a bag containing 16 blue balls and 14 yellow balls. Suppose we draw two balls at random, one after the other without replacement. Let’s define:

Event B = the first ball is blue

Event A = the second ball is blue

What will be the joint probability of A and B?

Solution

From the wording of the question, we can calculate the conditional probability P(A|B):

The probability that the first ball to be drawn is blue, P(B) = \(\cfrac {16}{30}\)

The probability that the second ball to be drawn is blue given the first one is also blue, P(A | B) = \(\cfrac {15}{29}\)

Thus,

$$ \begin{align*} P(AB) & = P(A | B)P(B) \\ & = \cfrac {15}{29} * \cfrac {16}{30} \\ & =\cfrac {240}{870} \\ & =\cfrac {8}{29} \\ \end{align*} $$

Addition Rule

We use the addition rule to assess the probability that events A or B occur:

$$ \text P(\text{A or B}) = \text P(\text A) + \text P(\text B) – \text P(\text {AB}) $$

Example: Addition rule

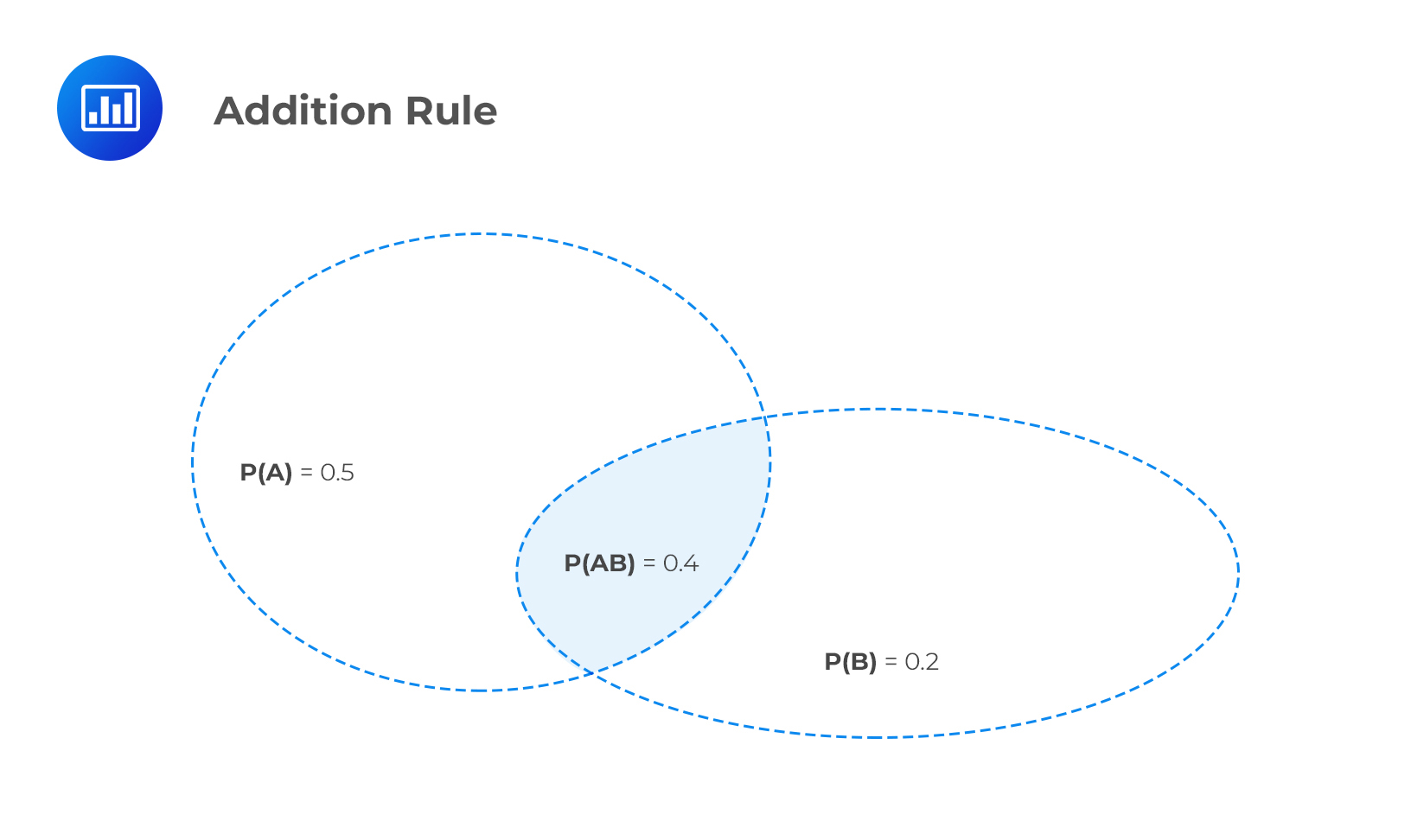
Suppose the probability of relaxed import restrictions is 0.5 and the probability of a price war is 0.2. If the joint probability of relaxed import restrictions and a price war is 0.4, what is the probability of relaxed trade restrictions or a price war?

Solution

$$ \text P(\text{A or B}) = 0.5 + 0.2 – 0.4 = 0.3 $$

Note: If two events are mutually exclusive, then:

\( \text P(\text{A or B}) = \text P(\text A) + \text P(\text B)\) since the joint probability would be (and is always) zero.

Total Probability Rule

Suppose we have a set of mutually exclusive and exhaustive events B₁, B₂, B₃…B_n.

We can determine the unconditional probability of an event, given the conditional probabilities:

$$ \text P(\text A) = \text P(\text A | \text B_1)\text P(\text B_1) + \text P(\text A | \text B_3)\text P(\text B_3) + … + \text P(\text A | \text B_n)\text P(\text B_n) $$

Perhaps an example will help you understand the concept:

Example: Total Probability Rule

Suppose a local authority subdivides a forest into three regions, B₁, B₂, and B₃. Assume the area covered by each region is 50km², 65km², and 74km^2, respectively. What is the total forest area, A?

The solution is simple: we just add the respective areas:

$$ 50 + 65 + 74 = 189 \text{ km}^2 $$

This is the idea behind the law of total probability. First, the total forest area is replaced by P(A). Then, we add the probability of A that falls in each partitions B₁, B₂, and B₃.