Application of Probability Rules

Probability rules are the concepts and facts that must be taken into account while evaluating the probabilities of various events. The CFA curriculum requires candidates to master 3 main rules of probability. These are the multiplication rule, the addition rule, and the law of total probability. Let’s now look at each rule in detail.

Multiplication Rule

We use the multiplication rule to determine the joint probability of two events, \(P(AB)\). A joint probability is the probability of two events happening together. For example, we may be interested in the probability that both gas prices and bus fares will increase simultaneously.

Mutually Exclusive Events

If two events are mutually exclusive, then they cannot occur together. Therefore, we say that such events have zero joint probability.

Non-mutually Exclusive Events

For non-mutually exclusive events, the multiplication rule states that:

$$ P(AB) = P(A | B)P(B) $$

Example: Multiplication Rule

Let’s assume we have a bag containing 16 blue and 14 yellow balls. Further, assume that we randomly draw two balls, one after the other, without replacement. Let’s define:

Event B = The first ball is blue.

Event A = The second ball is blue.

What will be the joint probability of A and B?

Solution

From the wording of the question, we can calculate the conditional probability \(P(A|B)\) as:

The probability that the first ball to be drawn is blue, P(B) = \(\cfrac {16}{30}\).

The probability that the second ball to be drawn is blue, given that the first one is also blue, P(A | B) = \(\cfrac {15}{29}\).

Therefore,

$$ \begin{align*} P(AB) & = P(A | B)P(B) \\ & = \cfrac {15}{29} × \cfrac {16}{30} \\ & =\cfrac {240}{870} \\ & =\cfrac {8}{29} \\ \end{align*} $$

Addition Rule

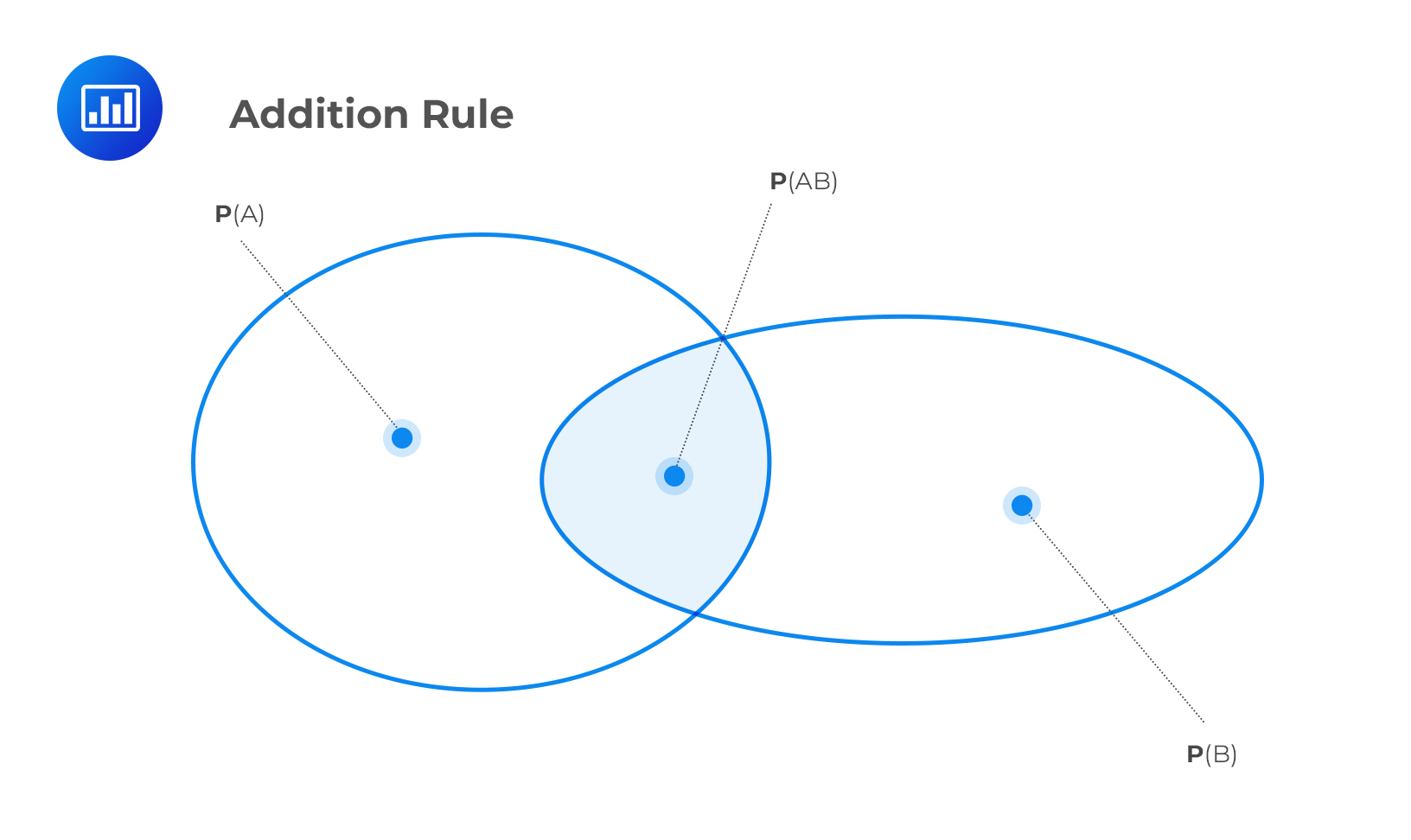
We use the addition rule to assess the probability that events A or B occur.

Mutually Exclusive Events

If A and B are mutually exclusive events:

$$ \text P(\text{A or B}) =\text P(\text A) + \text P(\text B) $$

Non-Mutually Exclusive Events

If A and B are non-mutually exclusive events:

$$ \text P(\text{A or B}) =\text P(\text A) + \text P(\text B) – \text P(\text {AB}) $$

This is because we have to remove one of the two instances of the intersection of A and B, as shown in the following figure.

Example: Addition Rule

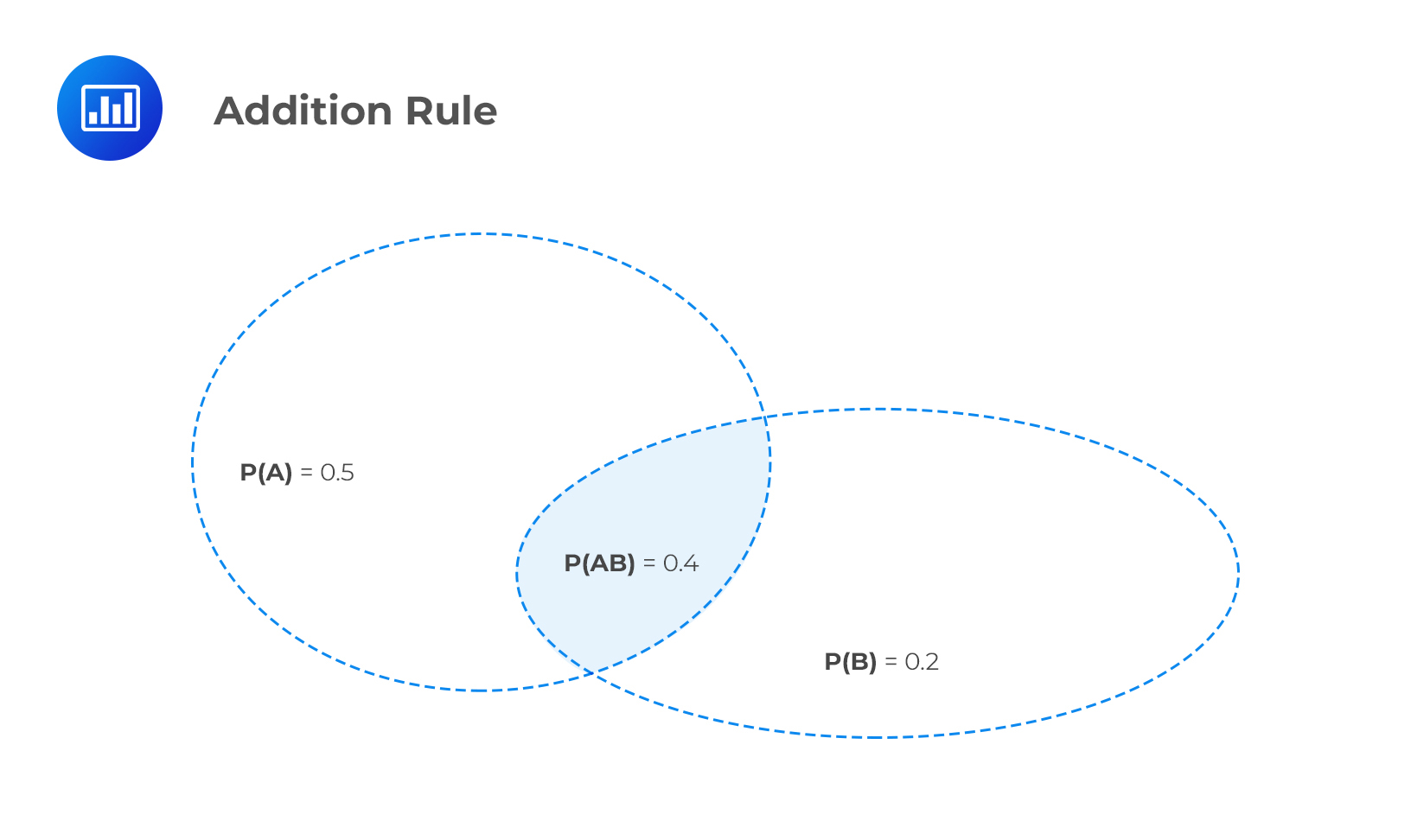
Assume that the probability of relaxed import restrictions is 0.5 and the probability of a price war is 0.2. If the joint probability of relaxed import restrictions and a price war is 0.4, what is the probability of relaxed trade restrictions or a price war?

Solution

$$ \begin{align} \text P(\text{A or B}) &= \text P(\text A) + \text P(\text B) – \text P(\text {AB}) \\ & = 0.5 + 0.2 – 0.4 = 0.3 \end{align} $$

Total Probability Rule

Suppose we have a set of mutually exclusive and exhaustive events B₁, B₂, B₃…B_n.

We can determine the unconditional probability of an event, given the conditional probabilities:

$$ \text P(\text A) = \text P(\text A | \text B_1)\text P(\text B_1) + \text P(\text A | \text B_3)\text P(\text B_3) + … + \text P(\text A | \text B_n)\text P(\text B_n) $$

Perhaps an example will help you understand the concept:

Example: Total Probability Rule

Suppose a local authority subdivides a forest into three regions, B₁, B₂, and B₃. Assume that each region covers 50km², 65km², and 74km², respectively. What is the total forest area?

Solution

We simply add the respective areas:

$$ 50 + 65 + 74 = 189 \text{ km}^2 $$

Question

An analyst analyzed defaults of one hundred and fifty corporate bonds, investment grade, and non-investment grade. The following table summarizes the results.   

$$ \begin{array}{l|c|c|c}\\ {}&\textbf{Bonds Default}&\textbf{Bonds did not}&\textbf{Total}\\ {}&{}&\textbf{default}&{}\\ \hline \text{Non-investment}&60&15&75\\ \text{grade bonds}&{}&{}&{}\\ \hline \text{Investment grade}&10&65&75\\ \text{bonds}&{}&{}&{}\\ \hline \text{Total}&70&80&150\\ \end{array} $$

If one bond from the sample of 150 bonds is selected at random, determine the probability that the bond defaulted given that it was non-investment grade:

1. 46.67%.
2. 80.00%.
3. 81.23%.

Solution

The correct answer is B.

The number of bonds that were defaulted and were non-investment grade was 60. The number of bonds that were non-investment grades was 75.

So, the probability that the bond defaulted, given that the bond did not default = 60 / 75 = 0.8 = 80%.

A is incorrect. It represents the probability of bonds defaulted out of the total sample of 150 bonds (70 / 150).

C is incorrect. It represents the probability that the bond was investment grade, given that the bond did not default. The number of bonds that did not default and were investment grade is 65. The number of bonds that did not default is 80.  So the probability that the bond was investment grade given that the bond did not default = 65 / 80 = 81.23%.