One-tailed vs. Two-tailed Hypothesis Testing

A one-tailed test (one-sided test) is a statistical test that considers a change in only one direction. In such a test, the alternative hypothesis either has a < (less than sign) or > (greater than sign), i.e., we consider either an increase or reduction, but not both.

Breaking Down a One-tailed Test

A one-tailed test directs all the significance level (α) to the testing of statistical significance in one direction. In other words, we aim at testing the possibility of a change in one direction and completely disregard the possibility of a change in the other direction.

If we have a 5% significance level, we shall allot 0.05 of the total area in one tail of the distribution of our test statistic.

Examples: Hypothesis Testing

Let us assume that we are using the standardized normal distribution to test the hypothesis that the population mean is equal to a given value X.  Further, let us assume that we are using data from a sample drawn from the population of interest. Our null hypothesis can be expressed as:

$$ H_0: \ \mu = X $$

If our test is one-tailed, the alternative hypothesis will test if the mean is either significantly greater than X or significantly less than X, but NOT both.

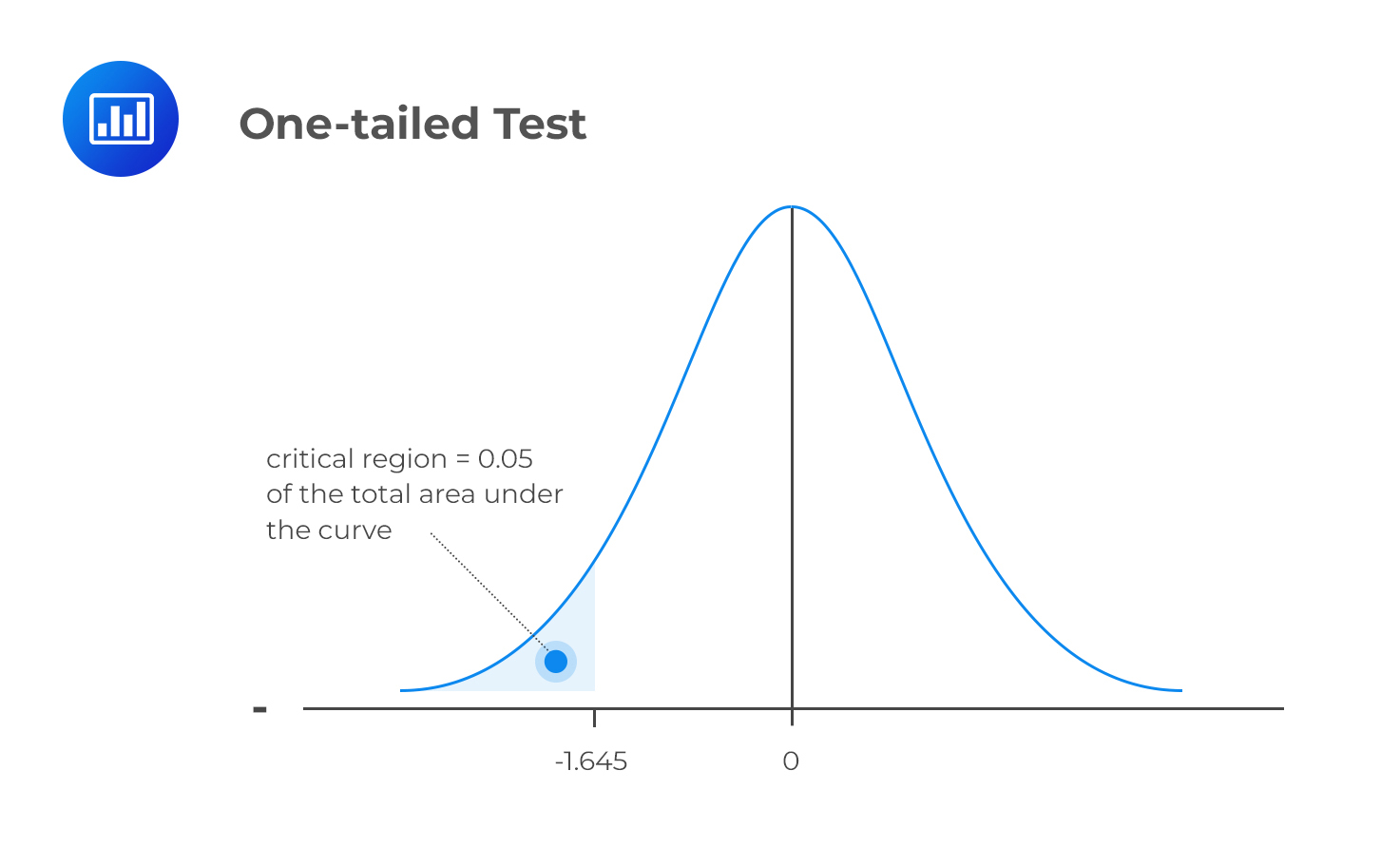
Case 1: At the 95% Confidence Level

$$ H_1: \ \mu < X $$

The mean is significantly less than X if the test statistic is in the bottom 5% of the probability distribution. This bottom area is known as the critical region (rejection region). We will reject the null hypothesis if the test statistic is less than -1.645.

Case 2: Still at the 95% Confidence Level

$$ H_1: \  \mu > X $$

We would reject the null hypothesis only if the test statistic is greater than the upper 5% point of the distribution. In other words, we would reject H₀ if the test statistic is greater than 1.645.

A Two-tailed Test

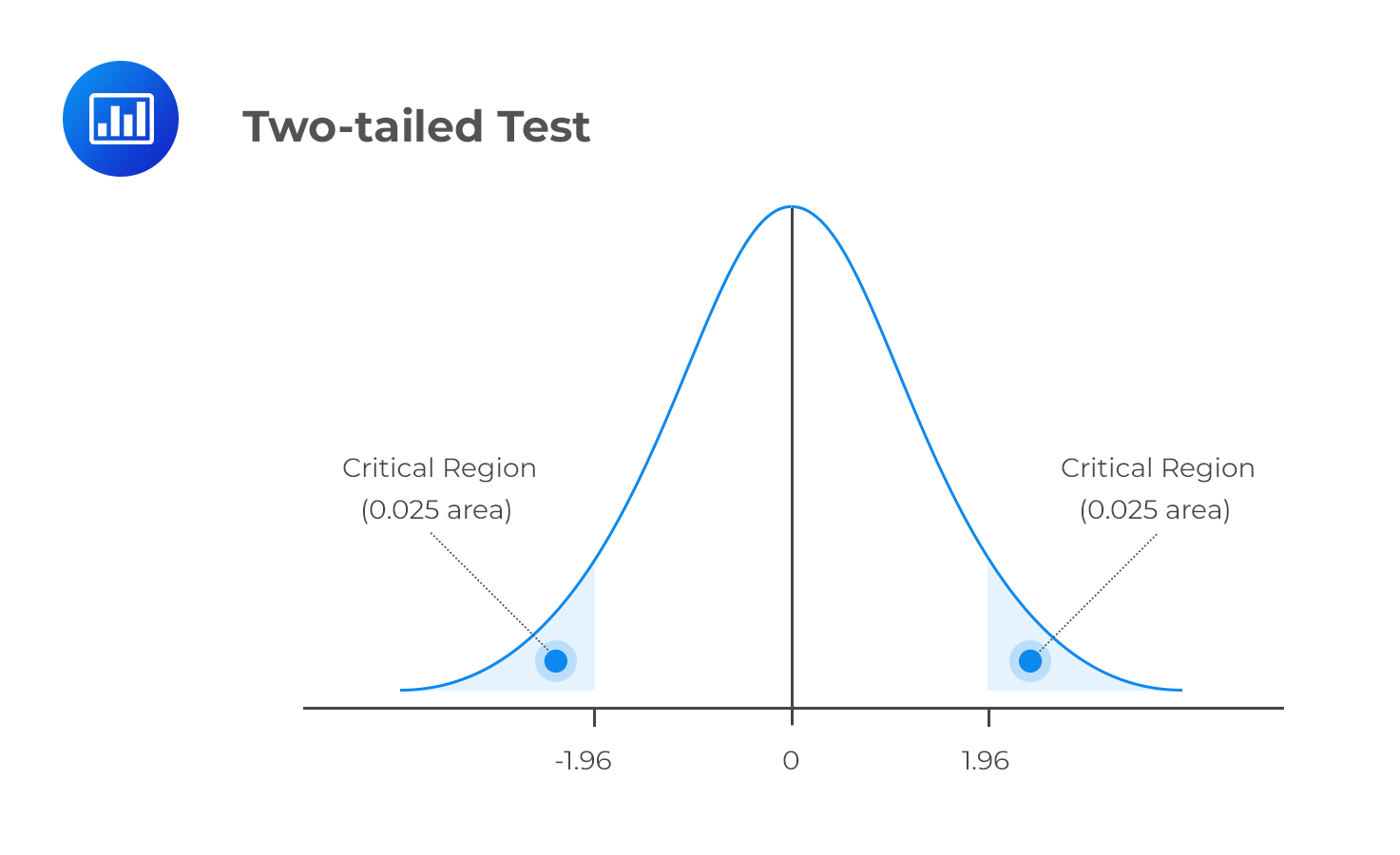
A two-tailed test considers the possibility of a change in either direction. It looks for a statistical relationship in both the positive and negative directions of a distribution. Therefore, it allows half the value of α to test statistical significance in one direction and the other half to test the same in the opposite direction. A two-tailed test may have the following set of hypotheses:

$$ H_0: \mu = X $$

$$ H_1: \mu \neq X $$

Refer to our earlier example. If we were to carry out a two-tailed test, we would reject H₀ if the test statistic turned out to be less than the lower 2.5% point or greater than the upper 2.5% point of the normal distribution.