Calculating Probabilities Given the Di ...
We can calculate and interpret probabilities of random variables that assume either the... Read More
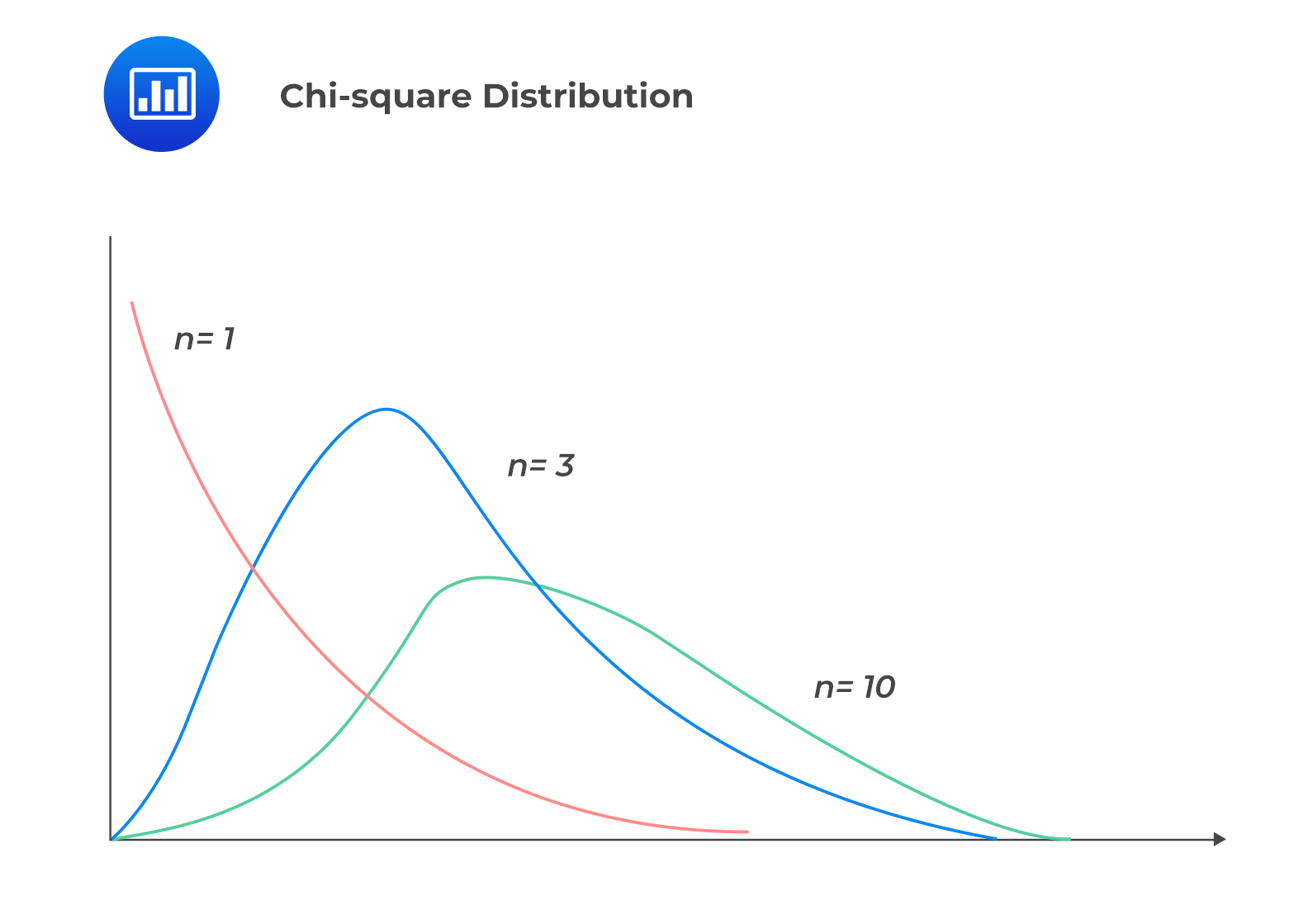
A chi-square distribution is an asymmetrical family of distributions. A chi-square distribution with \(v\) degrees of freedom is the distribution of the sum of the squares of \(v\) independent standard normally distributed random variables. Intuitively, chi-square distributions take only non-negative random variables.
A chi-square distribution is used to test the variance of a population that is distributed normally.
In a summary, the following are the properties of a chi-square distribution:
An F-distribution is used to test the equality of variances of two normally distributed populations from two independent random samples.
The following are the properties of an F-distribution:
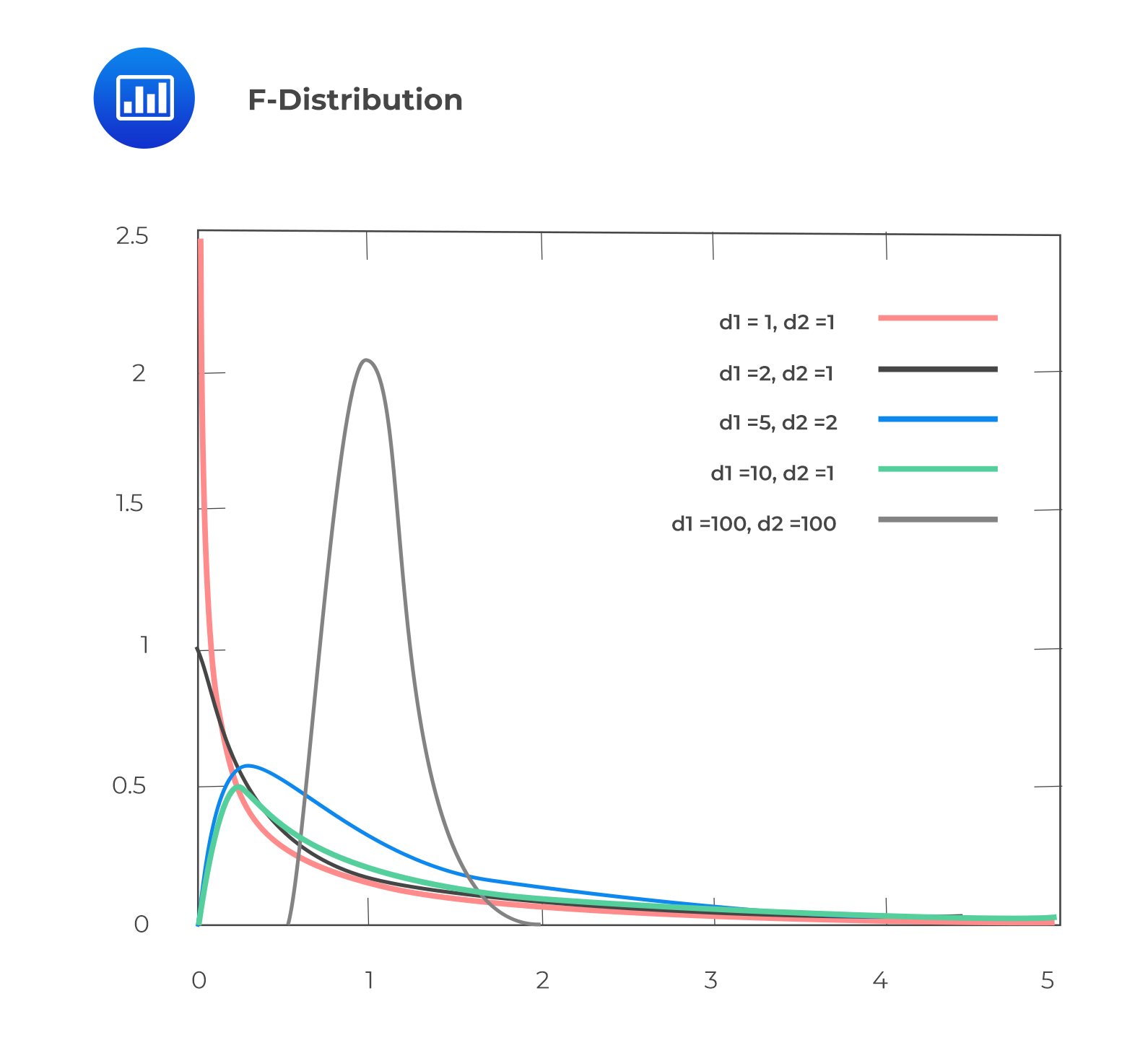
The F-distribution is the ratio of two chi-square distributions with degrees of freedom \(m\) and \(n\), respectively, where each chi-square has first been divided by its degrees of freedom, i.e.,
$$
F=\frac{\left(\frac{\chi_{1}^{2}}{m}\right)}{\left(\frac{\chi_{2}^{2}}{n}\right)}
$$
Where \(m\) is the numerator degrees of freedom and \(n\) is the denominator degrees of freedom.
Question
Which of the following are most likely common characteristics of F-distribution and chi-square distribution?
- Both can take only positive value.
- Both are defined by two parameters.
- Both are negatively skewed distributions.
Solution
The correct answer is A.
Both F-distribution and chi-square distribution can only take non-negative values.
B is incorrect. A chi-square distribution is defined by one parameter (i.e., n-1 degrees of freedom), while an F-distribution is defined by parameters, i.e., degrees of freedom of the numerator (m) and degrees of freedom of the denominator (n).
C is incorrect. Both the F-distribution and the chi-square distribution are positively skewed distributions.
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.