Optimal Portfolios

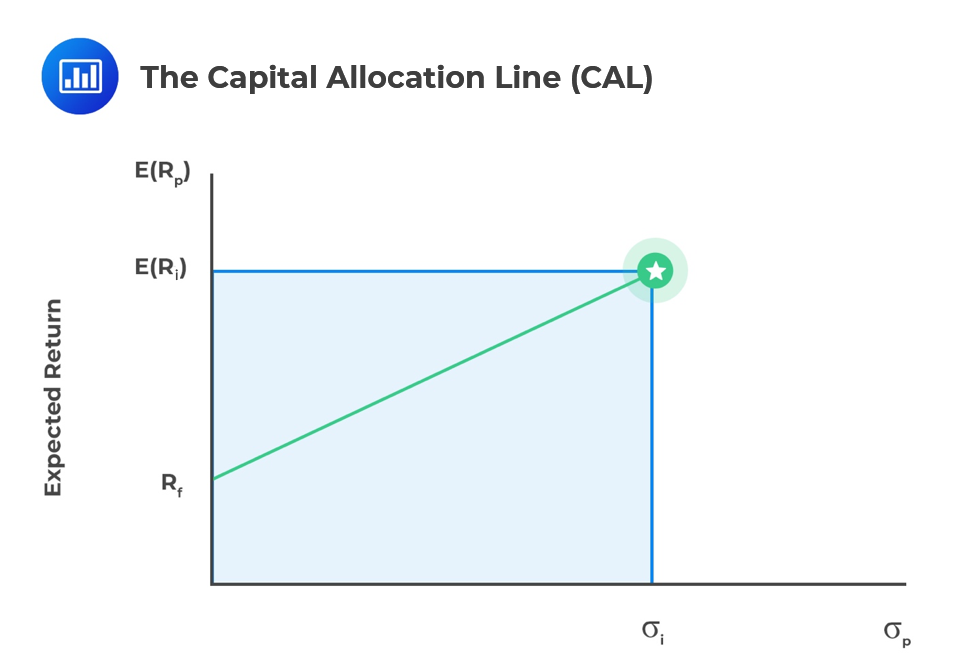
Risk-free assets are usually government-issued with no risk. When you combine them with risky assets, you create a capital allocation line on a graph. This line connects the best risky portfolio to the risk-free asset.

The Two-fund Separation Theorem

The two-fund separation theorem says all investors, no matter their preferences or wealth, use two funds: a risk-free one and a portfolio of risky assets. This splits portfolio building into two steps: first, we pick the best mix of risky assets based on their characteristics. Then, we decide how much to allocate to the risk-free asset based on the investor’s risk preference. Combining the risk-free asset with the risky portfolio makes the capital allocation line (CAL) on a graph.

Investor Preferences

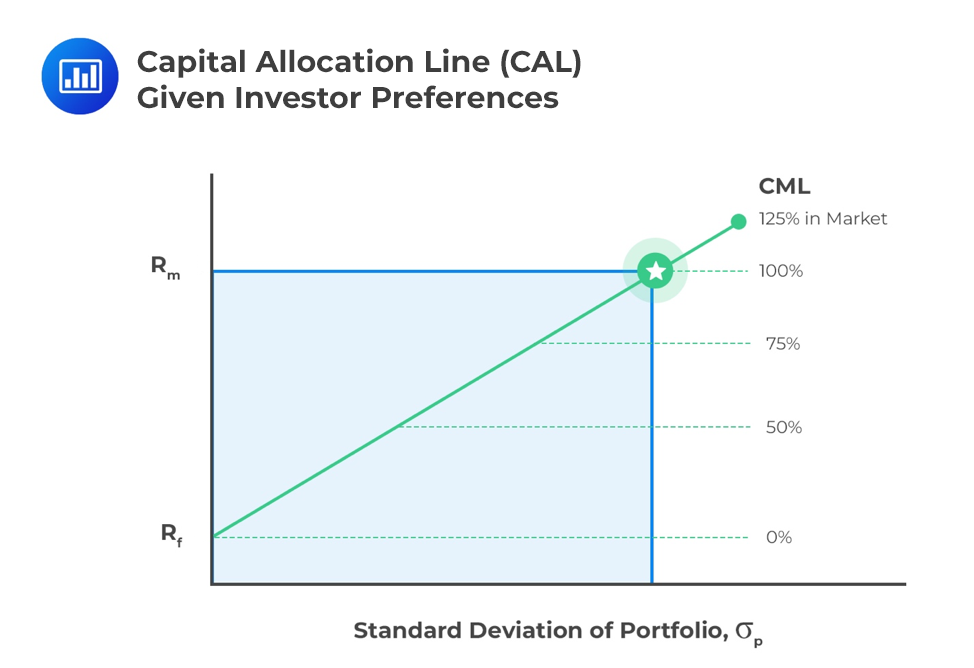
A highly risk-averse investor may choose to invest only in a risk-free asset. On the contrary, a less risk-averse investor may have a small portion of their wealth invested in the risk-free asset and a large portion invested in the risky portfolio. An investor with a high-risk tolerance may, in fact, choose to borrow from the risk-free asset and invest in a risky portfolio. This enables the investor to invest more than 100% of their assets and create a leveraged portfolio.

Utility and Indifference Curves

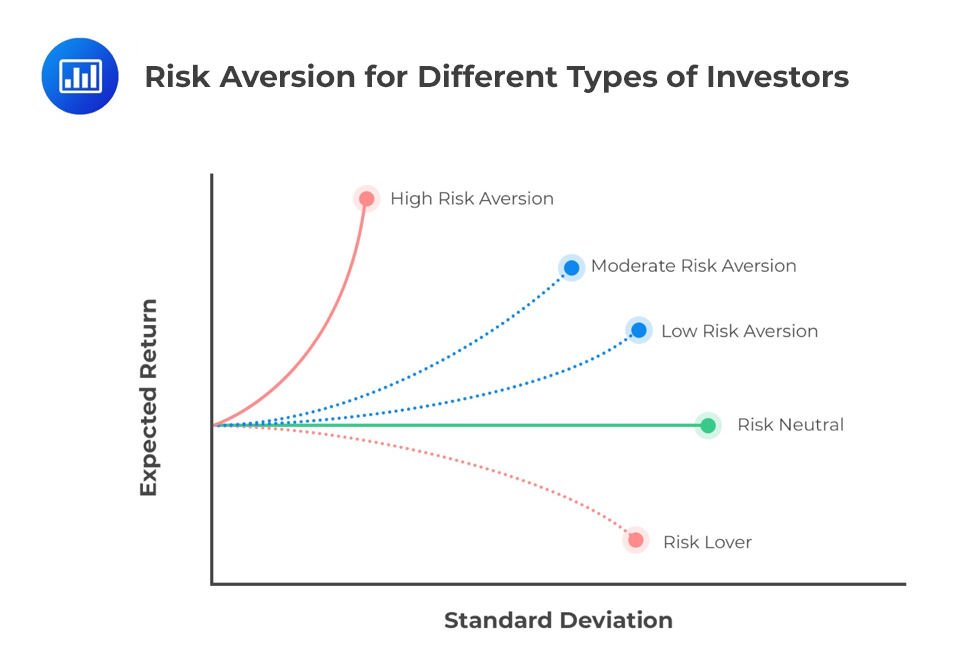
Utility is a measure of relative satisfaction that an investor derives from different portfolios. We can generate a mathematical function to represent this utility that is a function of the portfolio’s expected return, the portfolio variance, and a measure of risk aversion.

$$\text{U}=\text{E(r)}-\frac{1}{2}\sigma^2$$

Where:

U = Utility.

E(r) = Portfolio expected return.

A = Risk aversion coefficient.

\(\sigma^2\) = portfolio variance.

To determine risk aversion (A), we measure the marginal reward an investor needs in order to take more risk. A risk-averse investor will need a high-margin reward for taking more risks. The utility equation shows the following:

• Utility can be positive or negative – it is unbounded.
• High returns add to utility.
• High variance reduces utility.
• Utility does not measure satisfaction but can be used to rank portfolios.

The risk aversion coefficient, A, is positive for risk-averse investors (any increase in risk reduces utility). It is 0 for risk-neutral investors (changes in risk do not affect utility) and negative for risk-seeking investors (additional risk increases utility).

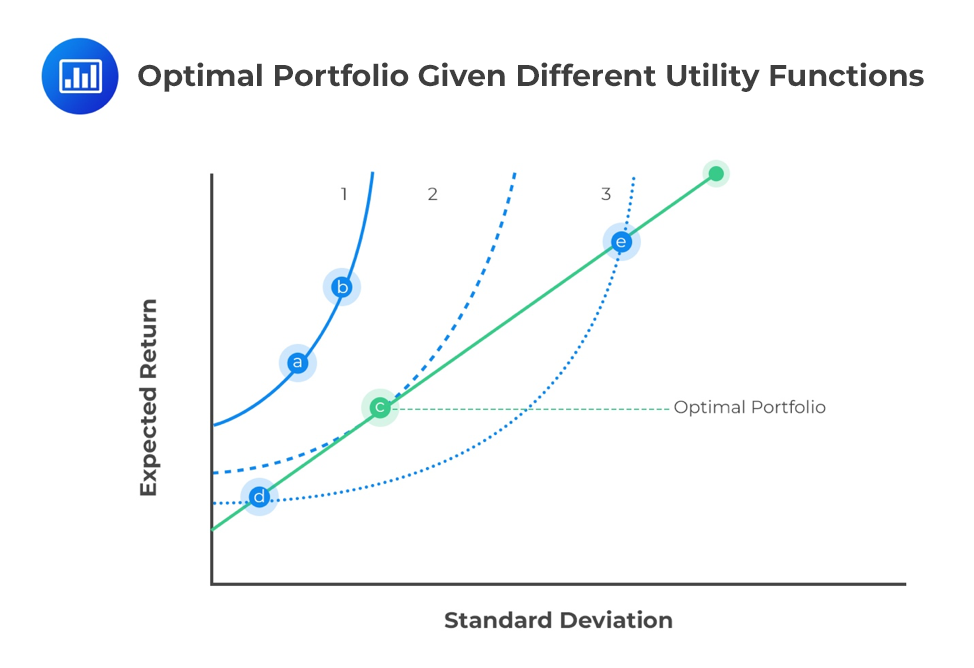
An indifference curve plots the combination of risk and returns that an investor would accept for a given level of utility. For risk-averse investors, indifference curves run “northeast” since an investor must be compensated with higher returns for increasing risk. It has the steepest slope. A more risk-seeking investor has a much flatter indifference curve as their demand for increased returns as risk increases is much less acute.

We can overlay an investor’s indifference curve with the capital allocation line to determine their optimal portfolio.

Question

Using the utility function \(\text{U}=\text{E(r)}-\frac{1}{2}\sigma^2\) and assuming A = -4, which of the following statements best describes the investor’s attitude to risk?

A. The investor is risk-neutral.

B. The investor is risk-averse.

C. The investor is risk-seeking.

Solution

The correct answer is C.

A negative risk aversion coefficient (A = -4) means the investor receives a higher utility (more satisfaction) for taking more portfolio risk. A risk-averse investor would have a risk aversion coefficient greater than 0, while a risk-neutral investor would have a risk aversion coefficient equal to 0.