Spot Curve, Yield Curve on Coupon Bonds, Par Curve, and Forward Curve

Yields-to-maturity for zero-coupon government bonds could be analyzed for a full range of maturities called the government bond spot curve (or zero curve). Government spot rates are assumed to be risk-free.

Spot Curve

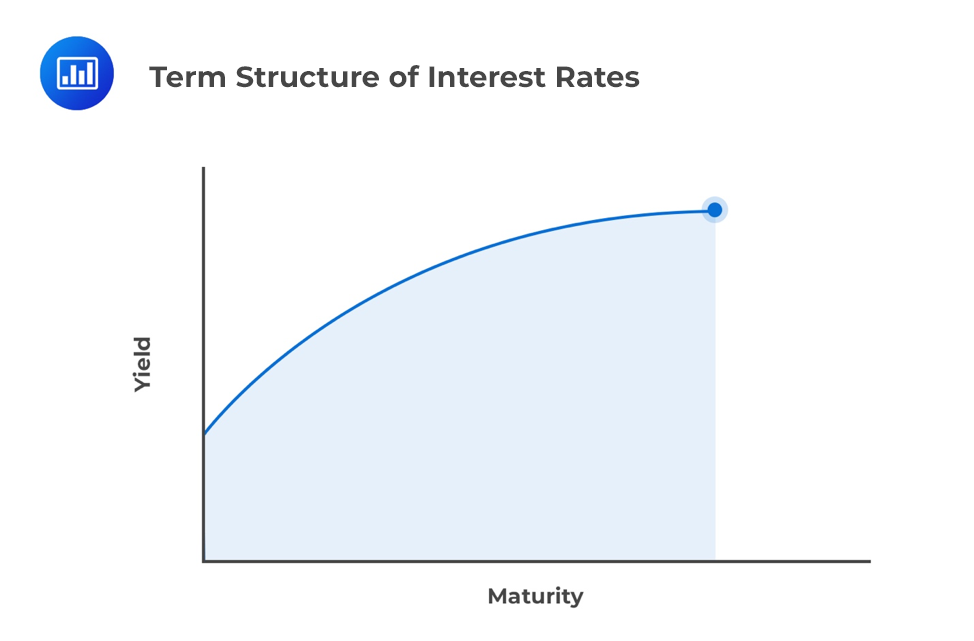
The spot curve is upward sloping and flattens for longer times-to-maturity. As a result, longer-term government bonds usually have higher yields than shorter-term bonds. The hypothetical spot curve is ideal for analyzing the maturity structure because it meets the “all other things being equal” assumption.

Par Curve

The par curve is dirrefent from the spot curve because it is a sequence of yields-to-maturity and each bond is priced at par value. The par curve is obtained from the spot curve. All bonds on the par curve are supposed to have the same credit risk, periodicity, currency, liquidity, tax status, and annual yields. Between coupon payment dates, the flat price (not full price) is equal to par value.

Obtaining Par Rates from Spot Rates

Since the par curve is a sequence of yields-to-maturity and each bond is priced at par value, the formula to obtain par rates is as follows.

\(100=\frac { PMT }{ { (1+{ Z }_{ 1 }) }^{ 1 } } +\frac { PMT }{ { (1+{ Z }_{ 2 }) }^{ 2 } } +…+\frac { PMT + Principal }{ { (1+{ Z }_{ N }) }^{ N } } \)

Where Z_N = the spot rate at time N

Example: Obtaining Par Rates from Spot Rates

Assuming that the 1-year and 2-year spot rates on government bonds are 5.25% and 5.75% respectively:

• the 1-year par-rate is 5.250%;

$$100=\frac { PMT+100 }{ 1.0525 } ;\quad PMT=5.25$$

• the 2-year par-rate is 5.736%.

$$100=\frac { PMT }{ 1.0525 } +\frac { PMT+100 }{ { 1.0575 }^{ 2 } } ; \quad PMT=5.736$$

Par Curve

The forward curve is a series of forward rates, each of which has the same time frame. We will talk at length about forward rates in the next learning objective.

Question

The yield curve derived from a sequence of yields-to-maturity on bonds where each bond is priced at par value is most likely called the:

1. par curve and all bonds on this curve are supposed to have the same annual yields.
2. forward curve and all bonds on this curve are supposed to have the same periodicity.
3. flat curve and all bonds on this curve are supposed to have the same liquidity and similar tax status.

Solution

The correct answer is A.

The par curve is a sequence of yields-to-maturity and each bond is priced at par value. All bonds on the par curve are supposed to have the same credit risk, periodicity, currency, liquidity, tax status, and annual yields.