Par and Forward Rates

Par Rates

A par rate is the yield-to-maturity that equates the present value of a bond’s cash flows to its par value (typically \(100\%\) of face value). Spot rates play a pivotal role in determining par rates. For a bond to be priced at par, its coupon rate and yield-to-maturity must be identical. This is depicted in the equation:

\[100 = \frac{PMT}{\left( 1 + z_{1} \right)^{1}} + \frac{PMT}{\left( 1 + z_{2} \right)^{2}} + \ldots + \frac{PMT + 100}{\left( 1 + z_{N} \right)^{N}}\]

Here, PMT represents the periodic payment, and \(z_{1},z_{2},\ldots,z_{N}\) are the sequence of spot rates for respective periods. By solving for \(PMT\), we obtain the yield-to-maturity that would make the bond trade at par, which is the par rate.

Example: Calculating Par Rate Given Spot Rates

Given the following spot rates for government bonds. Note that these are effective annual rates:

$$\begin{array}{l|c} \textbf{Term} & \textbf{Spot Rate} \\ \hline 1-Year & 4.50\% \\ 2-Year & 4.90\% \\ 3-Year & 5.25\% \\  \end{array}$$

One-Year Par Rate

Given the spot rate for one year is \(4.50\%\), the one-year par rate will also be \(4.50\%\).

\[100 = \frac{PMT + 100}{(1.0450)^{1}}\]

Two-Year Par Rate:

Using the spot rates for one year and two years, we can derive the two-year par rate:

\[100 = \frac{PMT}{(1.0450)^{1}} + \frac{PMT + 100}{(1.0490)^{2}}\]

PMT has been calculated as 4.8904, which translates to a two-year par rate of 4.8904%.

Three-Year Par Rate

Using the spot rates for one, two, and three years:

\[100 = \frac{PMT}{(1.0450)^{1}} + \frac{PMT}{(1.0490)^{2}} + \frac{PMT + 100}{(1.0525)^{3}}\]

PMT has been calculated as 5.2252, which translates to a three-year par rate of 5.2252%.

Forward Rates

Forward rates, often termed implied forward rates or forward yields, act as breakeven reinvestment rates. They establish a connection between the return on an investment in a shorter-term zero-coupon bond to the return on a longer-term zero-coupon bond. The most common market practice is to name forward rates by, for instance, “2y5y”, which means “2-year into 5-year rate”. The first number refers to the length of the forward period from today, while the second number refers to the tenor or time-to-maturity of the underlying bond.

Forward rates can be derived from spot rates and vice versa. The general formula to compute an implied forward rate between two periods is:

\[\left( 1 + Z_{A} \right)^{A} \times \left( 1 + IFR_{(A,B – A)} \right)^{(B – A)} = \left( 1 + Z_{B} \right)^{B}\]

Here, \(IFR_{(A,B – A)}\) denotes the implied forward rate for a bond beginning at time \(t = A\) and maturing at t=B. \(Z_{A}\) and \(Z_{B}\) represent spot rates for periods \(A\) and \(B\), respectively.

The following figure demonstrates the implied forward rates:

• The blue segment (from \(t = 0\) to \(t = A\) ) represents investing at the spot rate \(Z_{A}\) for \(A\) periods.
• The green segment (from \(t = A\) to \(t = B\) ) represents investing at the implied forward rate \(IFR_{(A,B – A)}\) for \(B – A\) periods.
• The red segment at the bottom (spanning the entire timeline) signifies that the compounded return of the above two rates is equivalent to investing at the spot rate \(Z_{B}\) for the entire \(B\) periods.

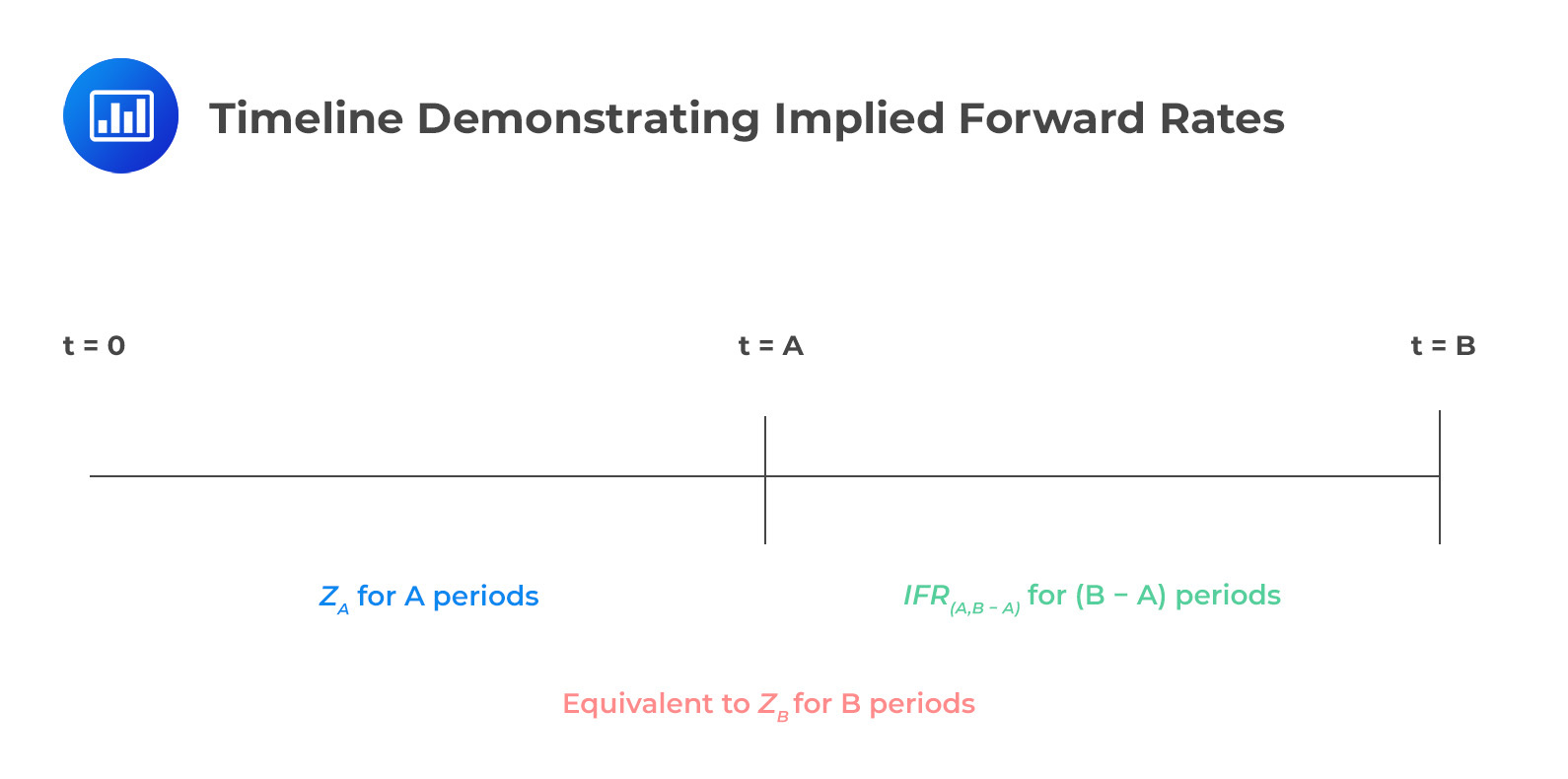
Forward rates are pivotal for investors and analysts as they provide insights into market expectations of future interest rate movements. They serve as breakeven rates, implying that if an investor’s expectations align with the forward rate, they would be indifferent between investing in a longer-term bond now or investing in shorter-term bonds successively.

Example: Calculating Implied Forward Rates from Spot Rates

Suppose that the yields-to-maturity on five-year and seven-year zero-coupon bonds are 4.85% and 5.45%, respectively, stated on a quarterly bond basis. An analyst wants to know the “5y2y” implied forward rate, which is the implied two-year forward yield five years into the future.

Given:

• \(A = 20\) (periods, since 5 years \(\times 4\) quarters per year)
• \(B = 28\) (periods, since 7 years \(\times 4\) quarters per year)
• \(B – A = 8\) (periods)
• \(z_{20} = \frac{0.0485}{4}\) (per period)
• \(z_{28} = \frac{0.0545}{4}\) (per period)

Let’s solve for \(IFR_{20,8}\) (the implied forward rate from period 20 to period 28).

Formula:

\[\left( 1 + z_{20} \right)^{20} \times \left( 1 + IFR_{20,8} \right)^{8} = \left( 1 + z_{28} \right)^{28}\]

\[\left( 1 + \frac{0.0485}{4} \right)^{20} \times \left( 1 + IFR_{20,8} \right)^{8} = \left( 1 + \frac{0.0545}{4} \right)^{28}\]

\[\left( 1 + \frac{0.0485}{4} \right)^{20} \times \left( 1 + IFR_{20,8} \right)^{8} = \left( 1 + \frac{0.0545}{4} \right)^{28}\]

\[IFR_{20,8} = \ 1.738\%\]

The “5y2y” implied forward rate is approximately 1.738% on a quarterly basis. Annualized, the “5y2y” implied forward yield is 7.13%.

Calculating Spot Rates from Forward Rates

Suppose the current forward curve for one-year rates is as follows:

$$\begin{array}{|c|c|} \hline \textbf{Time Period} & \textbf{Forward Rate} \\ \hline 0y1y & 1.50\% \\ 1y1y & 2.20\% \\ 2y1y & 2.80\% \\ \hline \end{array}$$

The provided rates are expressed on an annual basis with a period of one year, making them effective yearly rates. The initial rate, termed “0y1y,” represents the spot rate for one year. The subsequent rates are forward rates for one-year durations. Using these rates, the spot curve can be determined by taking the geometric average of the forward rates. The two-year implied spot rate can be calculated as:

\[(1.0150 \times 1.0220) = \left( 1 + z_{2} \right)^{2}\]

where \(z_{2}\) is the two-year implied spot rate.

\[z_{2} = 1.84940\%\]

Using this, and the 2y1y forward rate, we can then determine the three-year implied spot rate:

\[(1.0150 \times 1.0220 \times 1.0280) = \left( 1 + z_{3} \right)^{3}\]

where \(z_{3}\) is the three-year implied spot rate.

\[z_{3} = 2.16529\%\]

Suppose an analyst needs to value a three-year, \(2.50\%\) annual coupon payment bond that has the same risks as the bonds used to obtain the forward curve. Using the implied spot rates, we can determine the value of the bond.

\[PV = \frac{PMT}{\left( 1 + z_{1} \right)^{1}} + \frac{PMT}{\left( 1 + z_{2} \right)^{2}} + \ldots + \frac{PMT + 100}{\left( 1 + z_{N} \right)^{N}}\]

\[PV = \frac{2.5}{(1.0150)^{1}} + \frac{2.5}{(1.084940)^{2}} + \frac{2.5 + 100}{(1.0216529)^{3}}\]

\[PV = 100.993\ \]

This bond can also be valued using the forward rates and generate the same result.

Bond Pricing Using Forward Rates

Bonds can also be valued using forward rates. The bond’s future cash flows are discounted at the product of the sequence of one-year forward rates leading up to each cash flow. The summation of these discounted cash flows gives the bond’s price. The bond price remains consistent regardless of whether spot or forward rates are used.

Example: Bond Pricing Using Forward Rates

Suppose the current forward curve for one-year rates is as follows:

$$\begin{array}{|c|c|} \hline \textbf{Time Period} & \textbf{Forward Rate} \\ \hline 0y1y & 1.50\% \\ 1y1y & 2.20\% \\ 2y1y & 2.80\% \\ \hline \end{array}$$

Suppose an analyst needs to value a three-year, \(2.50\%\) annual coupon payment bond that has the same risks as the bonds used to obtain the forward curve. Determine the value of the bond using the forward rates above.

\[PV = \frac{2.5}{(1.0150)^{1}} + \frac{2.5}{(1.0150 \times 1.0220)} + \frac{2.5 + 100}{(1.0150 \times 1.0220 \times 1.0280)}\]

\[PV = 100.993\ \]

Question

Given a three-year spot rate of 3.5% and a four-year spot rate of \(4\%\), what is the one-year forward rate three years from now (3yly)?

1. 2.720%
2. 3.75%
3. 5.515%

Solution

The correct answer is C.

Using the formula:

\[\left( 1 + Z_{A} \right)^{A} \times \left( 1 + IFR_{A,B – A} \right)^{B – A} = \left( 1 + Z_{B} \right)^{B}\]

Where \(A = 3,B = 4,Z_{3} = 3.5\%\), and \(Z_{4} = 4\)%

\[(1 + 0.035)^{3} \times \left( 1 + IFR_{3,1} \right)^{1} = (1 + 0.04)^{4}\]

Solving for \(IFR_{3,1}\) will give 5.515%