Macaulay, Modified, and Effective Durations

The duration of a bond measures the sensitivity of the bond’s full price (including accrued interest) to changes in the bond’s yield-to-maturity or, more generally, changes in benchmark interest rates.

Bond duration estimates changes in bond price assuming that variables other than yield-to-maturity or benchmark rates are held constant. Further, time-to-maturity is also unchanged.

Generally, the higher the duration, the higher the drop in the price of the bond as interest rates rise. As a general rule, for every 1% change in interest rates, the price of a bond will change by approximately 1% in the opposite direction for every year of duration. For example, if a 10-year bond has a duration of 7 years, its price will rise by about 7% (= 1% × 7) if the interest rate drops by a percentage point (100 basis points). Similarly, its price will fall by about 7% if the interest rate rises by that amount.

There are two types of bond durations; yield duration and curve duration. The yield duration is defined as the sensitivity of bond price with respect to its own yield-to-maturity. The curve duration, on the other hand, is defined as the sensitivity of bond price with respect to a benchmark yield curves such as a government yield curve, spot curve, or forward curve. However, the government par curve is the most oftenly used. The yield duration statistics are Macaulay Duration, Modified Duration, Money Duration, and Price Value of a Basis Point (PVBP).

Macaulay Duration

Macaulay Duration is the length of time taken by an investor to recover the money they invested in a bond through coupons and principal repayment. It attempts to measure the number of years it takes for an investor to recoup the bond’s price from the bond’s total cash flows.

It is calculated as a weighted average of times, j, at which the cash flows occur, where the weights are the percentage of the present value of the cash flow with respect to the sum of the present value of all the cash flows:

$$MacDur=\frac { \sum _{ j=1 }^{ N }{ \cfrac { { CF }_{ j } }{ { (1+i) }^{ j } } \times j } }{ \sum _{ j=1 }^{ N }{ \cfrac { { CF }_{ j } }{ { (1+i) }^{ j } } } } =\frac { \cfrac { { CF }_{ 1 } }{ { (1+i) }^{ 1 } } \times 1+\cfrac { { CF }_{ 2 } }{ { (1+i) }^{ 2 } } \times 2+…+\cfrac { { CF }_{ n } }{ { (1+i) }^{ n } } \times n }{ P } $$

Where:

CF_j = cash flow at time j

i = yield to maturity or market discount rate

P = price of the bond (present value of all cash flows)

Example of Macaulay Duration

Assume an investor buys a 6% annual payment bond with three years to maturity. The bond has a yield-to-maturity of 8% and is currently priced at 95 per 100 of par. Its Macaulay Duration can be computed as follows:

$$MacDur=\frac{\frac{6}{1.08}\times 1+\frac{6}{1.08^2}\times 2+\frac{106}{1.08^3}\times 3}{95}=2.82$$

This means that it will take an average 2.82 years for the bondholder of this 3-year bond to receive its estimated cash flows.

Modified Duration

Modified Duration (ModDur) is an extension of Macaulay Duration and helps to measure the sensitivity of a bond to changes in interest rates. Its calculation requires a simple adjustment to the Macaulay Duration.

The calculation of the Modified Duration (ModDur) statistic of a bond requires a simple adjustment to Macaulay Duration as such:

$$ModDur=\frac { MacDur }{ (1+y) } $$

Where y = yield to maturity or required yield.

For instance, the modified duration of a 5-year, 8% annual payment bond is 3.786.

$$ModDur=\frac { 4.247 }{ 1.1218 } =3.786$$

This shows that for every 1 percent movement in interest rates, the bond in this example would inversely move in price by 3.786 percent.

Approximate Modified Duration

It is easy to calculate the Modified Duration once we have the Macaulay Duration. Even without the latter, we can still approximate the Modified Duration by estimating the slope of the line tangent to the price-yield curve. This can be achieved using the equation below:

$$ \text{Approximate Modified Duration} =\frac { { PV }_{ – }-{ { P }V_{ + } } }{ 2\times \Delta yield\times { PV }_{ 0 } } $$

Where:

\({ PV }_{ – }\) = price of the bond when the yield is decreased

\({ PV }_{ + }\) = price of the bond when the yield is increased

\({ PV }_{ 0 }\) = initial price of the bond

\(\Delta yield\) = expected change in yield

Note: \({ PV }_{ – }\) and \({ PV }_{ – }\) are the full prices, including accrued interest.

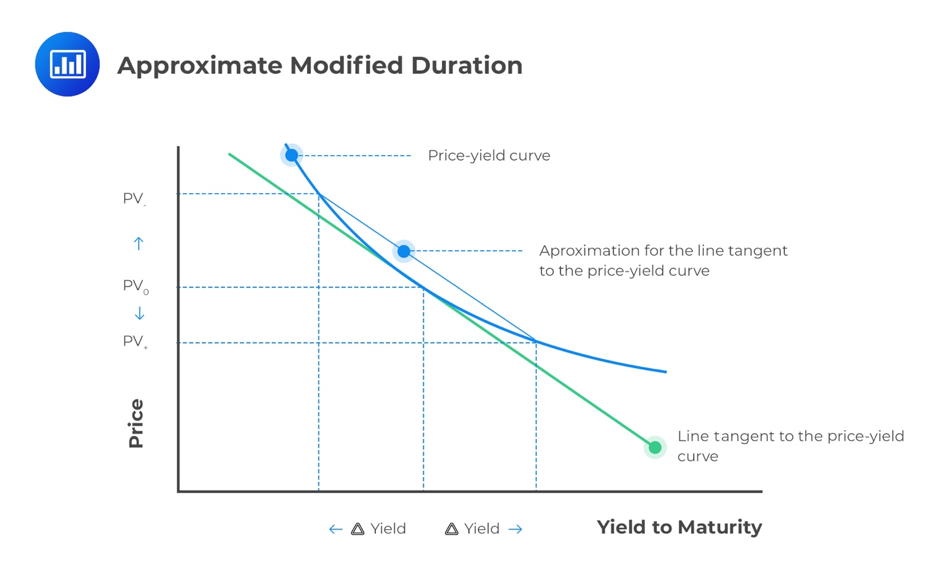
To estimate the slope, we shift the yield-to-maturity up and down by the same amount, i.e., yield. The bond prices corresponding to the shifted yields to maturity are then noted.

Approximate Macaulay Duration

Since

$$ModDur=\frac { MacDur }{ (1+y) } $$

… the Macaulay Duration can be approximated as the approximate Modified Duration multiplied by one plus the yield per period:

$$ \text{Approximate Macaulay Duration} = \text{Approx. ModDur} × (1 + r) $$

Example: Approximate Modified and Macaulay Duration

An investor buys a three-year bond with a 5% coupon rate paid annually. The bond, with a yield-to-maturity of 4%, is purchased at a price of 102.425632 per 100 of par value. Assuming a 5-basis point change in yield-to-maturity, determine the approximate modified duration and Macaulay Duration of the bond.

Lower yield to maturity by 5 bps to 3.95%:

$${ PV }_{ – }=\frac { 5 }{ { (1+0.0395) }^{ 1 } } +\frac { 5 }{ { (1+0.0395) }^{ 2 } } +\frac { 100+5 }{ { (1+0.0395) }^{ 3 } } =102.916613$$

Increase yield to maturity by 5 bps to 4.05%:

$${ PV }_{ + }=\frac { 5 }{ { (1+0.0405) }^{ 1 } } +\frac { 5 }{ { (1+0.0405) }^{ 2 } } +\frac { 100+5 }{ { (1+0.0405) }^{ 3 } } =102.633837$$

$${ PV }_{ 0 }=102.425632; \quad \Delta yield=0.0005$$

Approximate Modified Duration \(=\frac { 102.916613-102.633837 }{ 2\times 0.0005\times 102.425632 } =2.761\)

Approx. MacDur = Approx. ModDur × (1 + r) = 2.761 × 1.04 = 2.87

Therefore, the investor knows that the weighted average time to receipt of interest and principal payments is 2.87 years (the Macaulay Duration) and that the estimated loss in the bond’s market value is 2.761% (the Modified Duration) if the yield-to-maturity were to suddenly go up by 1% from 4% to 5%.

Effective Duration

Effective duration of a bond is the sensitivity of the price of the bond to a change in a benchmark yield curve.

$$EffDur=\frac { { PV }_{ – }-{ { P }V_{ + } } }{ 2\times \Delta curve\times { PV }_{ 0 } } $$

Where \({ PV }_{ 0 }\), \({ PV }_{ – }\), and \({ PV }_{ + }\) are the prices of the bond at time 0, immediately before the change in yield, and immediately after the change in yield, respectively.

Example: Effective Duration

When the government par curve is raised and lowered by 30 bps, the new full prices for the callable bond are 99 and 103, respectively. If the present value of the bond is 101, i.e., \({ PV }_{ 0 }=101.00\), \({ PV }_{ + }=99.00\),  \({ PV }_{ – }=103.00\), and \(\Delta yield=0.003\), i.e., 30 basis points, determine the effective duration of the bond.

$$EffDur=\frac { 103-99 }{ 2\times 0.0030\times 101 } =6.601$$

Note: although they appear similar, the approximate Modified Duration and Effective Duration are different. The Modified Duration is a yield duration statistic that measures interest rate risk with reference to a change in the yield-to-maturity (ΔYield) of the bond. On the other hand, effective duration is a Curve Duration statistic that measures interest rate risk in terms of a parallel shift in the benchmark yield curve (ΔCurve).

Effective Duration is the best duration measure of interest rate risk when valuing bonds with embedded options because such bonds do not have well-defined internal rates of return (yield-to-maturity). Therefore, yield durations statistics such as Modified and Macaulay Durations do not apply.

Quick Facts on Duration

• As maturity increases, duration increases, and the bond’s volatility increases.
• As the coupon rate of a bond increases, its duration decreases, and the bond becomes less volatile.
• Duration and interest rates have an inverse relationship: as interest rates increase, duration decreases, and the bond’s sensitivity to further interest rate increases goes down.

Question

An investor buys a 5% annual payment bond with 3 years to maturity. The bond has a yield to maturity of 7.5% and is currently priced at 93.5 per 100 of par. The bond’s Macaulay Duration is closest to:

1. 2.65
2. 2.75
3. 2.85

Solution

The correct answer is C.

\(MacDur=\frac { \frac { 5 }{ { 1.075 }^{ 1 } } \times 1+\frac { 5 }{ { 1.075 }^{ 2 } } \times 2+\frac { 105 }{ { 1.075 }^{ 3 } } \times 3 }{ 93.5 } =2.85\)