Features of a Fixed Income Security

Fixed-income securities are significant debt-financing tools for both corporations and governments. They operate under standardized agreements where issuers raise funds for various financial needs. In return, investors provide capital and anticipate regular interest payments and the eventual return on their initial investment. These securities make up a range of corporate liabilities, each having distinct characteristics like different maturities, seniority levels, and currencies.

Fixed-income securities are distinctive from other liabilities as they involve cash-settled agreements with investors or banks. Governments typically use bond issuance as their primary financing strategy, though some also secure loans from international bodies like the IMF. A distinguishing characteristic of fixed-income securities from equities is their guaranteed periodic cash flows, offering investors regular income and capital return upon maturity.

Key Characteristics of Fixed-income Securities

Issuer

A bond’s issuer, whether it’s a national government, a local body, or a private corporation, is responsible for making all interest and principal payments. Sovereign bonds usually carry the least risk due to governmental backing.

Maturity

This signifies the end date when the issuer completes its payments to bondholders. Securities with a maturity period of one year or less are considered money market securities, while those extending beyond a year are capital market securities. Perpetual bonds, which do not have a definite maturity, are also a unique class of bonds.

Principal

This is the amount that the issuer agrees to repay to investors at the end of the bond’s lifespan. Some securities may distribute principal repayment over time rather than in one lump sum at maturity.

Coupon Rate and Frequency

Bond interest can be classified as fixed, variable, or part of a single payment at maturity. Fixed-coupon bonds involve regular payments at specific intervals (monthly, quarterly, semi-annual, or annual), with corporate bonds typically paying semiannually. Floating-rate notes (FRNs) have variable interest determined by combining a market reference rate (MRR) and a credit spread. Zero-coupon bonds, on the other hand, do not pay periodic interest. Instead, they pay interest along with the principal at maturity and are usually issued at a discount to par value.

$$ \text{Interest expense} =\frac{\text{Par Value of the bond} \times \text{Coupon rate}}{\text{Frequency of payments}} $$

Seniority

In terms of repayment during liquidation or bankruptcy, senior debt takes precedence over other forms of debt. Junior or subordinated debts are repaid only after senior debts are settled.

Contingency Provisions

Bonds may include clauses for actions under certain circumstances. A contingency provision in bonds includes embedded options like call, put, and conversion to equity. These options cannot be traded separately from the bond but can be valued by comparing it with a similar bond without such provisions.

Yield Measures

The bond’s expected cash flows and its price can be used to determine yield measures like current yield and yield-to-maturity.

$$ \text{Current yield} =\frac{\text{Annual coupon}}{\text{Bond price}}\times100\% $$

Yield-to-maturity (YTM) is a more complex measure, calculated as the internal rate of return using the bond’s price and its coupon payments until maturity. It is normally expressed as an annual rate. If all assumptions hold (no default, holding until maturity, reinvesting at YTM), the investor’s rate of return will equal the bond’s YTM at the time of purchase.

Yield Curves

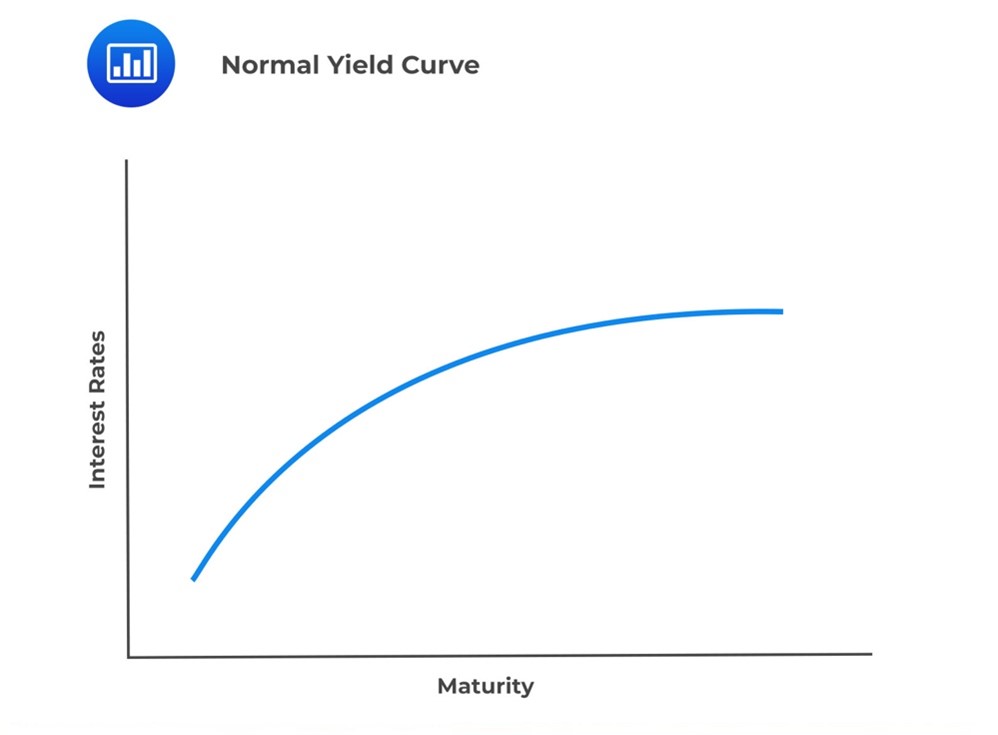
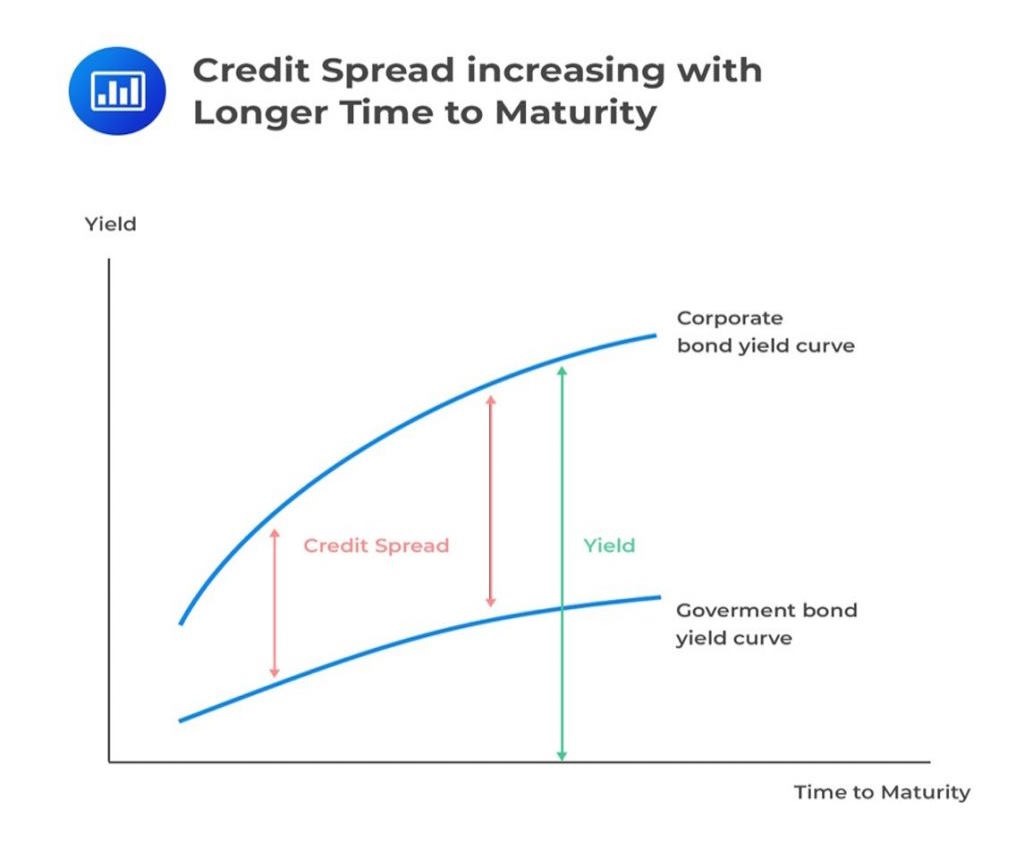
Plotting an issuer’s bonds against their yield-to-maturity and time-to-maturity gives us a yield curve. It is a useful tool for comparing the expected returns on different bonds issued by the same entity. Comparing this with the yield curve of a risk-free bond, like a sovereign bond, gives a measure of the credit risk of the bond.

This is demonstrated in the charts that follow.

Question 1

The coupon payment on a 3% coupon bond with a par value of $200,000 and a quarterly payment frequency is closest to:

1. $666.67.
2. $1500.00.
3. $24000.00.

Solution

The correct answer is B.

$$ \begin{align*} \text{Coupon payment} & =\frac{\text{Par Value of the bond} \times \text{Coupon rate}}{\text{Frequency of payments}} \\
\text{Coupon payment} & =\frac{\$200,000 \times 3\%}{4}=\$1,500 \end{align*} $$

Question 2

Calculate the annual interest payable for a USD 5 million FRN issued by a U.S. corporation, which pays quarterly interest equal to the three-month MRR plus 200 bps. If the three-month MRR is 1.75%, what is the corporation’s quarterly FRN coupon interest payable for the period?

1. $46,875.
2. $87,500.
3. $187,500.

Solution

The correct answer is C.

The FRN coupon consists of the MRR plus the issuer-specific spread.

$$ \begin{align*}
\text{FRN coupon} & = \text{MRR} + \text{Spread.} \\
\text{FRN coupon} & = 1.75\% + 2.00\%. \\
\text{FRN coupon} & = 3.75\%.
\end{align*} $$

$$ \text{Quarterly interest} = \$5,000,000 \times 3.75\% = \$187,500 $$