Corporate Issuer Credit Ratings
The major credit-rating agencies, Moody’s, Standard & Poor’s (S&P), and Fitch Ratings (“Fitch”),... Read More
The Modified Duration provides an estimate of the percentage price change for a bond given a change in its yield-to-maturity. A secondary effect is measured by the convexity statistic.
The true relationship between the bond price and the yield-to-maturity (YTM) is a curved (convex) line. The duration (in particular, money duration) estimates the change in bond price along with the straight line that is tangent to the curved line. For small yield-to-maturity changes, there is little difference between the lines. However, as the change in YTM grows larger, the difference becomes significant.
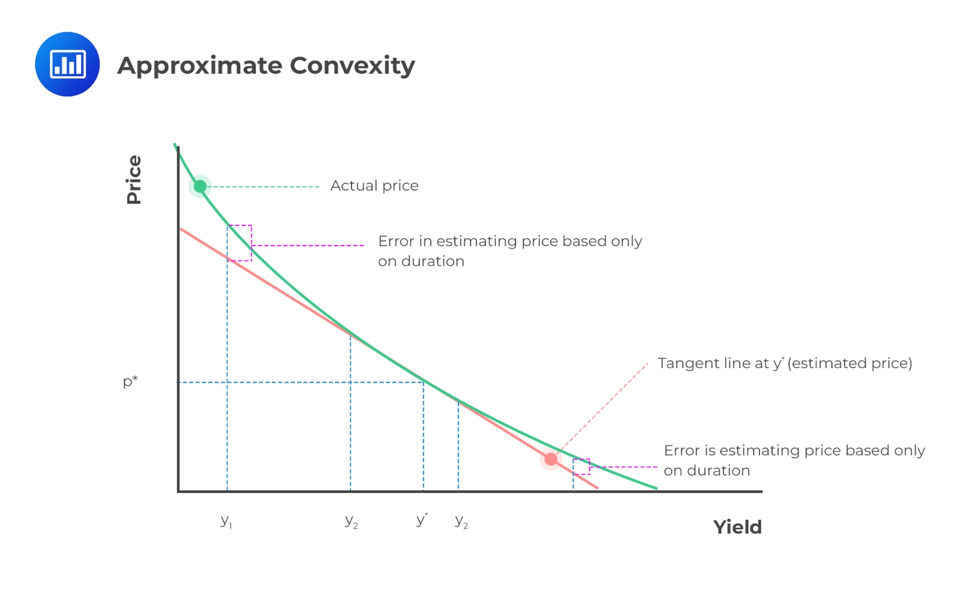
A convexity measure is used to improve the estimate of the percentage price change.
$$\%ΔPV^{FULL}≈(\text{-AnnModDur}×ΔYield)+(\frac{1}{2}×\text{AnnConvexity}×(ΔYield)^2)$$
The second bracketed expression is the convexity adjustment:
$$ \text{Convexity effect} ≈ \frac{1}{2}×\text{AnnConvexity}×(ΔYield)^2 $$
The convexity adjustment is the annual convexity statistic, AnnConvexity, times one-half, multiplied by the change in the yield-to-maturity squared. This amount adds to the linear estimate provided by the duration alone, which brings the adjusted estimate very close to the actual price on the curved line. The sign “≈” is used because the resulting adjusted price is just an estimate.
The effective convexity of a bond is a curve convexity statistic that measures the secondary effect of a change in a benchmark yield curve. Note that for bonds with somewhat unpredictable cash flows, we use effective duration to measure interest rate risk. Similarly, we use the effective convexity to measure the change in price resulting from a change in the benchmark yield curve for securities with uncertain cash flows. In fact, effective convexity is a secondary curve convexity statistic that measures the secondary effect of a change in the benchmark yield curve.
$$\text{Effective convexity}=\frac{PV_{-}+PV_{+}-2PV_{0}}{(ΔCurve)^2PV_{0}}$$
Where:
PV– = Price if yield curve declines by Yield (parallel shift)
PV+ = Price if yield curve increases by Yield (parallel shift)
PV0 = Initial bond price
ΔCurve = Change in yield on the benchmark curve
The main difference between approximate and effective convexity is that approximate convexity is based on a yield to maturity change, whereas effective convexity is based on a benchmark yield change.
Here are a few quick facts about bonds with embedded options:
For a zero-coupon bond, the exact convexity statistic in terms of periods is given by:
$$\text{Convexity}_{\text{zero-coupon bond}}=\frac{[N-\frac{t}{T}]×[N+1-\frac{t}{T}]}{(1+r)^2}$$
Where:
N = number of periods to maturity as of the beginning of the current period;
t/T = the fraction of the period that has gone by; and
r = the yield-to-maturity per period.
Question
A bond has a convexity of 120. What is the convexity effect if there is a sudden interest rate change of 50 basis points?
- 0.003
- 0.0015
- 0.3
Solution
The correct answer is B.
\(\text{Convexity effect} ≈ \frac{1}{2}×\text{AnnConvexity}×(ΔYield)^2\)
\(0.0015≈ \frac{1}{2}×120×(0.005)^2\)