Annual Bond Yield: Different Compounding Periods

The yield on a bond is a measure of the return on investment, which depends on the interest rate and the frequency of compounding. Understanding how to calculate the annual yield for varying compounding periods is essential for investors to compare different investment options.

Periodicity and Annualized Yields

The periodicity of the annual rate refers to the number of interest periods in a year. It is a crucial factor in the calculation of the effective yield on a bond. The periodicity typically aligns with the frequency of coupon payments:

• Annual: Periodicity = 1.
• Semiannual: Periodicity = 2.
• Quarterly: Periodicity = 4

Calculating Future Value of Cash Flows

The future value (FV) of cash flows represents the total value of a series of payments at a future point in time. It is calculated using the formula:

$$ FV = FV(\text{rate}, \text{nper}, \text{pmt}, \text{pv}, \text{type}) $$

Where:

• \(\text{rate}\) is the periodic reinvestment rate.
• \(\text{nper}\) is the number of periods in a year.
• \(\text{pmt}\) is the rate per period.
• \(\text{pv}\) is the present value (optional).
• \(\text{type}\) indicates when payments occur (optional).

The following figure illustrates the Effective Annual Rate (EAR) for different compounding periods, emphasizing the subtle differences in yield:

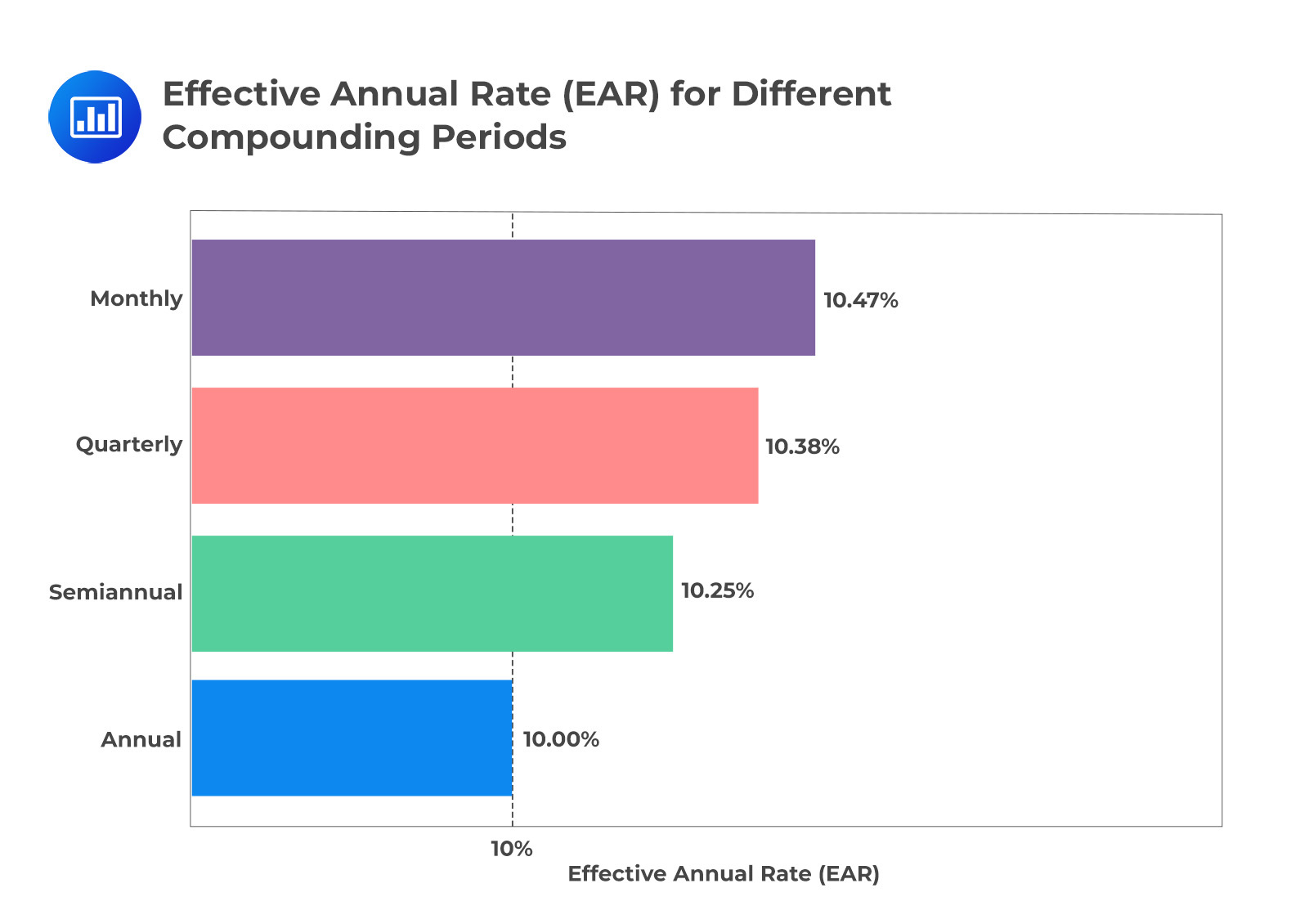
Though the differences between the EAR values may appear small, they reveal how the frequency of compounding affects the effective yield on an investment. These variations can have a significant impact over time, especially with large investments or longer investment horizons.

Investors can gain insights into the importance of compounding frequency when evaluating different investment options. It allows for a nuanced understanding and comparison between bonds with different payment frequencies, considering the subtle but meaningful variations in yield that arise from changes in compounding periodicity.

Periodicity Conversions

A crucial instrument in the study of fixed-income assets involves transforming an annualized yield from one compounding frequency to another. Such transformations are known as periodicity or compounding adjustments. The following equation is used to convert an annual percentage rate for periods per year, denoted, to an annual percentage rate for periods per year.

$$ (1 + \frac{APR_m}{m})^m = (1 + \frac{APR_n}{n})^n $$

Where:

• \(APR_m\) is the annual percentage rate for \(m\) periods per year.
• \(APR_n\) is the annual percentage rate for \(n\) periods per year.
• \(m\) is the number of periods per year in the original periodicity.
• \(n\) is the number of periods per year in the converted periodicity.

Example

An investor is considering a 3-year bond that pays a 6% annual coupon with a face value of $1,000. The bond is currently priced at $950. Calculate the effective annual rate of the bond at issuance assuming annual, semiannual, and quarterly compounding.

Solution

Parameters:

• Face Value (F): $1,000.
• Current Price (P): $950.
• Time to Maturity: 3 years.
• Coupon Rate: 6%.
• Coupon Payment: $60 (6% of $1,000).

Calculate the yield for Different Compounding Periods

Annual Compounding

\[950=\frac{60}{\left(1+r\right)^1}\ +\frac{60}{\left(1+r\right)^2}\ +\frac{1000+60}{\left(1+r\right)^3}\]

r has been calculated using Excel as 7.938%

Semi-annual compounding (n=2)

Convert from a periodicity of m = 1 to periodicities of n = 2 and n = 4

This converts the effective annual rate to semiannual and quarterly bond equivalent yield.

\[ \left(1+\frac{0.07938}{1}\right)^1=\left(1+\frac{APR_2\ }{2}\right)^2 \]
\[ \sqrt{\left(1.07938\right)}=1+\frac{APR_2}{2} \]
\[ APR_2\ =\ 7.786\% \]
\[ \left(1+\frac{0.07938}{1}\right)^1=\left(1+\frac{{APR}_2}{2}\right)^2 \]
Quarterly compounding (n=4)
\[ \left(1+\frac{0.07938}{1}\right)^1=\left(1+\frac{APR_4\ }{4}\right)^4 \]
\[ APR_4=7.712\% \]

Explanation

Annual Compounding: The bond yield is highest when compounded annually. This is because there is less frequent reinvestment of the coupon payments, leading to a lower accumulation of interest.

Semiannual and Quarterly Compounding: As the frequency of compounding increases, the YTM decreases slightly. This is due to the more frequent reinvestment of coupon payments, which compounds more often and thereby increases the effective yield of the bond.

Thus, varying compounding frequencies can affect the bond’s yield, usually leading to a decrease in YTM as the frequency increases.

Question

A yield of 2.432% compounded quarterly is closest to an effective annual rate of:

1. 0.430%.
2. 2.447%.
3. 2.454%.

The correct answer is C.

The effective annual rate assumes a single compounding period in a year (periodicity of 1). To convert from quarterly to annual compounding, we need to change from a periodicity of 4 to 1:

\[ \left(1+\frac{APR_m}{m}\right)^m=\left(1+\frac{APR_n}{n}\right)^n \]

\[ \left(1+\frac{0.02432}{4}\right)^4=\left(1+\frac{APR_1}{1}\right)^1 \]

\[ APR_1=2.454\% \]