Forward Contract

A forward contract is an over-the-counter (OTC) derivative contract.  In this contract, two parties agree that one party, the buyer (long), will purchase an underlying asset from the other party, the seller (short), at a later date at a fixed price (the forward price) agreed upon when the contract is initiated. A forward contract is suitable for hedging an existing or expected underlying exposure based on specified terms. For example, an importer may use a forward contract to hedge against foreign exchange by entering a forward contract to buy foreign currency to fulfill a future goods delivery contract.

Payoff Profile of a Forward Contract

Assume that we are currently at time \(t=0\), where the price of the underlying is \(S_0\). The forward contract expires at a future date \(t=T\), where the underlying price is now \(S_T\). The price \(S_T\) is unknown at the initiation of the contract. At time \(t=0\), the long (buyer) and the short (seller) agree that the seller will deliver the underlying asset for the price of \(F_0(T)\), the forward price, at time \(t=T\), the expiration date. However, an important element of a forward contract is that no money is exchanged when the contract is initiated. Thus, forward contracts can be considered to have zero value at the start and are neither assets nor liabilities. The value deviates from zero as the price of the underlying moves. The ability to “lock in” a future price for an asset has important practical benefits and is used as an instrument for financial speculation.

Outcomes of a Forward Contract at Maturity

If, at the expiration date, the current spot price is greater than the forward price \([S_T>F_0(T)]\), the buyer (long) receives a payoff of $$\text{Payoff}=S_T-F_0(T)$$ Intuitively, the short incurs a loss of \(-(S_T-F_0(T))\) because the seller must deliver an asset at \(S_T\) and receive less amount \(F_0(T)\). The table below gives a summary of the outcomes: $$\small{\begin{array}{c|c|c} \textbf{Outcome at Expiry} & \textbf{Buyer (long) Payoff} & \textbf{Seller (Short) Payoff} \\ \hline S_T>F_0(T)&[S_T -F_0(T)]>0 &[F_0(T)-S_T]<0 \\ \hline S_T<F_0(T)&[S_T-F_0(T)]<0 &[F_0(T)-S_T]>0\end{array}}$$ We can represent the above results  in a graph:

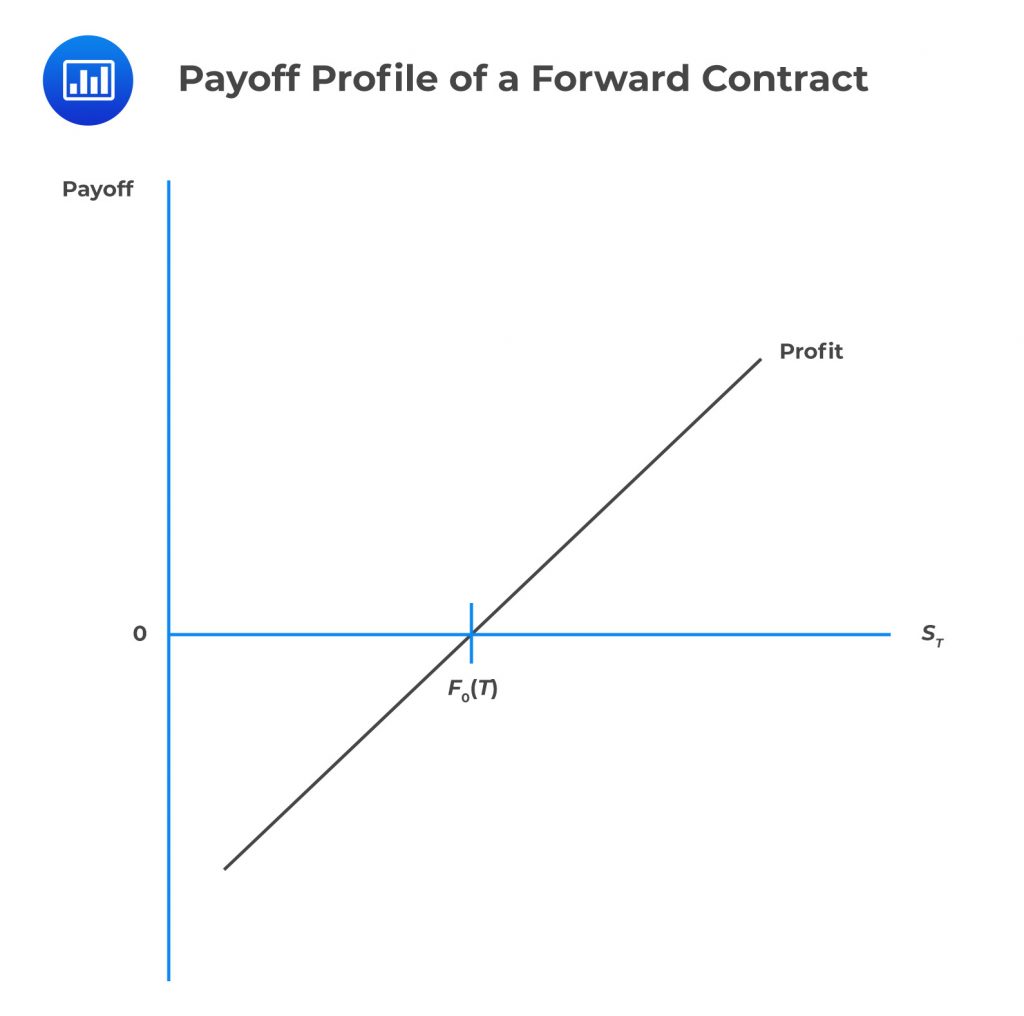
From the graph above, it is easy to see that the price of the forward contract is a linear function of the underlying. As such, forward commitments are also called linear derivatives.

Example: Calculating the Forward Contract

Minners Inc. enters a forward contract with a financial intermediary to buy 80 kilos of gold at USD 53,000 per kilo. The spot price of gold is USD 52,780 per kilo. How much will Minners Inc. pay (receive) to (from) the financial intermediary?

Solution

$$\begin{align*}\text{Payoff at maturity}&=S_T-F_0(T)\\&=52,780-53,000\\&=-\text{USD 220}\end{align*}$$ Therefore, Minners Inc. (buyer) must pay USD 17,600 \((= 80 × 220)\) to the financial intermediary (seller).

Futures Contracts

Futures contracts are a standardized variation of forward contracts. The buyer of the futures contracts agrees to buy the underlying in the future at a pre-agreed price (futures price). On the other hand, the seller agrees today to sell the underlying asset in the future at a  price agreed upon at the initiation of the contract. The exchange determines expiration dates, underlying assets, the size of the contracts, and other details. A distinguishing element of futures contracts compared to forward contracts is the mark-to-market feature (also called daily settlement), where the exchange determines an average of the final futures trades of the day (settlement price). Each party’s account in the transaction will be debited or credited with the losses or gains for the day.

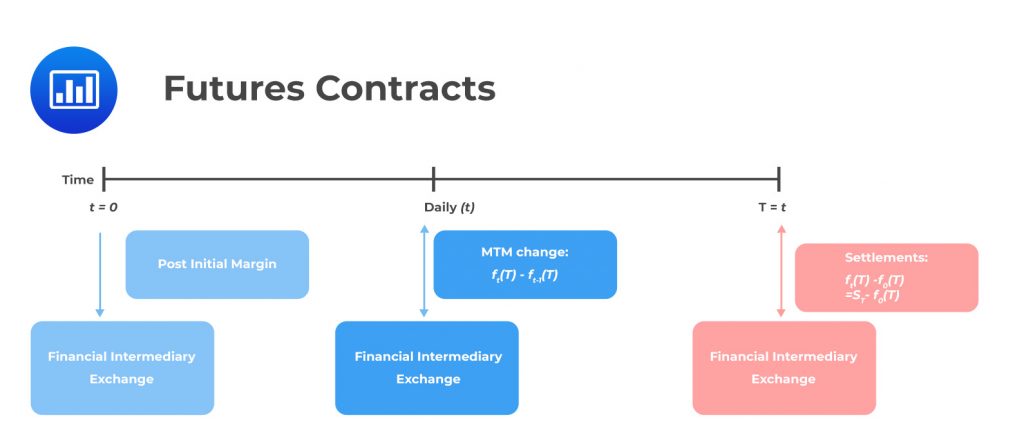
Like forward contracts, the payoff is based on the difference between the futures price and the underlying price at the expiration date. For example, from the buyer’s perspective, the payoff is given by: $$\text{Payoff}-S_T-F_0(T)$$ Additionally, the futures price converges towards the spot price at expiration. In cash-settled transactions, there is a final mark-to-market at expiration, with the futures price set to the spot price to ensure convergence:

Futures Margin and Settlement Process

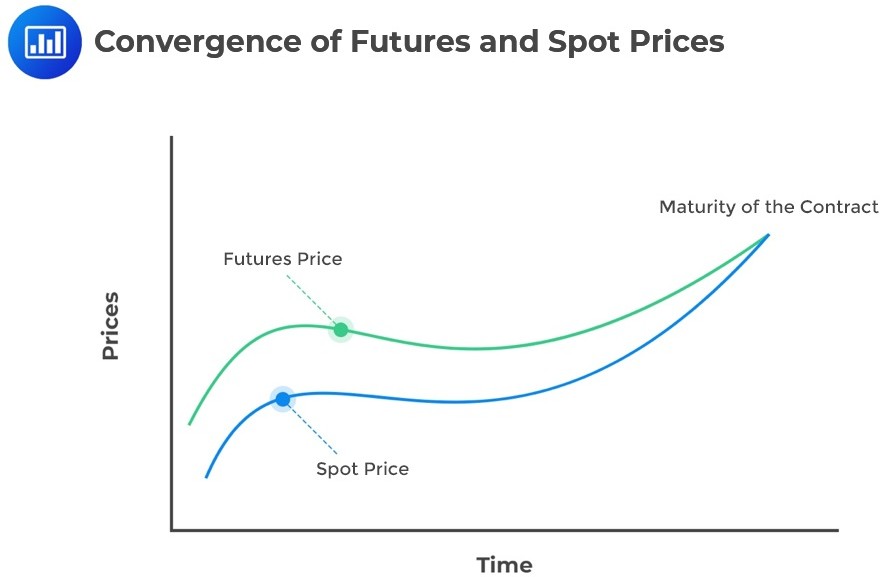
Denote the futures price by \(f_0(T)\) and the current spot price at expiry by \(S_T\). Note that, like forward contracts, no cash changes hands at the initiation of the futures contract. However, both counterparties must deposit the initial margin into a futures margin account at the exchange. The exchange uses the futures margin account to settle daily market changes. Special financial intermediaries usually execute futures contracts on behalf of the counterparties. When the futures margin account funds fall below the initial margin, the seller receives a margin call to top up the account back to the initial amount. The added sum is called the variation margin. If a counterparty cannot replenish the margin account, it must close out the contract as soon as possible and incur additional costs in the process. In extreme cases where a counterparty cannot meet the obligations, the exchange covers the losses through an insurance fund. At maturity, the outstanding contracts (collectively called open interest) are settled through cash or physical delivery (whichever is stated in the contract). However, a counterparty may elect to enter an offsetting future contract before expiration to close out a position.

How Exchanges Limit Losses Due to Defaults in Futures Contracts

An exchange might impose additional requirements to limit potential default-occasioned losses. These include:

• Increasing required margins: Due to an increase in price volatility.
• Price limits: Establishing a band relative to the previous day’s settlement price in which all trades take place.
• Circuit breaker: Stopping intraday trading for a short period if the price limit has been reached.

Futures Contracts Accounts (Summary)

Futures Margin Accounts

Futures margin accounts are transactional accounts of buyer and seller held by the exchange. If the end-of-day settlement price decreases, the buyer (long) loses money, which is charged from the margin account and transferred to the seller’s account (short). The opposite is true. Let’s assume that at maturity, the futures price is greater than the underlying price. In that case, the profit is transferred to the buyer’s account (short) from the seller’s (short) account, which equals total settlements.

Initial Margin

This is the minimum amount of money (typically less than 10% of the futures price) that is deposited by both parties to cover possible future losses.

Maintenance Margin

This refers to the sum of money (lower than the initial margin) that each party must maintain in the margin account from the initiation to the maturity of the trade.

Margin Call

This is the request to deposit additional funds (variation margin) into the account if it falls below the maintenance margin.

Example: Margin Call

Minners Inc. enters a 3-month futures contract on an exchange through a financial intermediary to buy 80 kilos of gold with an opening price of USD 53,000 per kilo. The exchange requires an initial margin of USD 127,200 and a maintenance margin of USD 115,750. Below is an excerpt of mark-to-market (MTM) details: $$\small{\begin{array}{c|c|c|c|c|c}\textbf{Day}&\textbf{Futures Price}&\textbf{Day Gain/Loss}&\textbf{Net Gain/Loss}&\textbf{Margin Balance}&{\textbf{Margin Call}\\ \textbf{Variation Margin}}\\ \hline \text{T}_{90}&$53,000&&&$127,200&\\ \hline \text{T}_{89}&$53,124&$9,920&$9.920&$137,120&\\ \hline \text{T}_{88}&$53,080&($3,520)&$6,400&$133,600&\\ \hline \text{T}_{87}&$52,600&($38,400)&($32,000)&$95,200&$32,000\\ \hline\text{T}_{88}&$53,024&$33,920&$1,920&$161,120& \\ \hline&&&& \\ \hline&&&&\\ \hline&&&&\\ \hline\text{T}&$53,129&$10,020&($2,020)&$134,125\end{array}}$$

Day 89:

• The gold futures price increases by USD 124, so the gain is \(\text{USD 9,920} (=80 × 124)\).
• \(\text{Margin balance} = \$127,200 + \$9,920 = $137,120\)
• No margin call since the margin balance is higher than the maintenance margin.

Day 87

• The gold futures price decreases by USD 480, so the loss is \(\text{USD 38,400} (=80 × 480)\).
• \(\text{Margin balance} = \$133,600 − \$38, 400 = \$95,200\) (below the maintenance margin).
• \(\text{Margin call amount (variation margin)} = \$127,200 − \$95,200 = \$32,000\)

Swaps

A swap is an over-the-counter derivative contract in which two parties agree to exchange a series of cash flows whereby one party pays a variable (floating) series that an underlying asset or rate will determine. The other party either pays  (1) a variable series determined by a different underlying asset or rate or (2) a fixed rate. For instance, in interest rate swaps, the floating rate payer pays a market reference rate (MRR) which resets every period, and the fixed rate payer pays a fixed-rate (swap rate), which is constant, as shown below.

As is the case in forwards and futures, no money changes hands at the initiation of the contract. However, as time passes and market conditions vary, the MTM value of the swap contract changes. Note that counterparties exchange a net payment on fixed-and floating payments. The counterparties privately negotiate the credit terms of a swap rate. The credit terms may range from uncollateralized exposure to margining like the futures contract. Swaps may be centrally settled between financial intermediaries by a central counterparty (CCP), where they involve margins like those of futures contracts. The notional amount is a sum of money that is used to calculate fixed and floating interest payments.

Example: Calculating Swap Contract Net Cashflow

FinnLay LTD has entered a 10-year interest rate swap with a financial institution with a notional amount of USD 100 million. The contract states that FinnLay signed to receive a semiannual USD fixed rate of 5% and, in turn, pay a semiannual market reference rate (MRR). For the first six months, MRR is 2%. Calculate the first swap cash flow.

Solution

The amount owed to FinnLay by the financial intermediary: \(\frac{5\%}{2}\times100m=2.5m\) Amount paid by FinnLay to the Financial intermediary: \(\frac{2\%}{2}\times100m=1.0m\) Therefore, the netting is: \(2.5m-1.0m=1.5m\) Net Result: Financial intermediary pays FinnLays USD 1.5 million after six months.

Common Features among Forwards, Futures, and Swaps

• Defined contract size.
• Defined underlying.
• There is one or more exchanges of cash flows or underlying on a given date or dates.
• The exchanges are based on pre-agreed prices.

Option Contracts

Options are derivative instruments that give the option buyer the right, but not the obligation, to buy (call) or sell (put) an asset from (or to) the option seller at a fixed price on or before expiration. In other words, options are contingent claims that give the option buyer the right but not the obligation to transact the underlying, and the option seller is obligated to meet the obligation chosen by the buyer. As such, the payoff of an option is positive or zero. However, the profit can be negative since it takes into account the payoff plus (minus) the premium received (paid) by (to) the option buyer (seller). If the option expires out-of-the-money, the seller of the option receives the full amount of the premium.

More on Options

When the option buyer decides to transact the underlying, it is referred to as exercising the option. The pre-agreed price at which the option buyer exercises the underlying is called the exercise price. It is the fixed price at which the underlying asset can be bought or sold at expiry. The option buyer pays the seller an option premium for the right to exercise the option in the future. It is the fair price of an option in a well-functioning market. The option buyer (long) is not obligated to exercise the option beyond the initial payment of the premium. Options can be traded on over-the-counter (OTC) markets or exchanges based on standardized terms. Options can be American options or European options. European-style options can only be exercised at expiry, while American-style options are exercisable before expiry. This reading primarily dwells on European options. There are two types of options: call option and put option. In call options, the buyer has the right but not the obligation to buy the underlying. On the other hand, in put options, the buyer has the right but not the obligation to sell the underlying. Consequently, the option will only be exercised if the payoff is positive; otherwise, the option expires worthless, and the buyer incurs a loss equal to the option premium. More information on payoff profile options is given in the next reading.

Question

Which statement is most accurate when the stock price is above the exercise price (S_T > X) on a put option at expiration? A. The option seller will suffer a loss equivalent to the difference between the stock price and the exercise price. B. The option buyer will suffer a loss equivalent to the difference between the stock price and the exercise price. C. The option seller will show a profit equivalent to the option premium amount, the option buyer will show a loss equivalent to the option premium amount.

Solution

The correct answer is C. If the stock price is above the exercise price at expiration, the put option expires out-the-money and is worthless. The option buyer has lost the premium paid while the option seller has made a gain equivalent to the premium received.