Solving Counting Problems through Labe ...
[vsw id=”hu47ZbsskEw” source=”youtube” width=”611″ height=”344″ autoplay=”no”] Counting problems involve determination of the exact... Read More
[vsw id=”KbEfz3KiJDo” source=”youtube” width=”611″ height=”344″ autoplay=”no”]
A cumulative distribution function, F(x), gives the probability that the random variable X is less than or equal to x:
$$ P(X ≤ x) $$
By analogy, this concept is very similar to the cumulative relative frequency.
A cumulative distribution is the sum of the probabilities of all values qualifying as “less than or equal to” the specified value. Perhaps an example will make this concept clearer.
Imagine flipping a coin three times. You would end up with the following probability distribution of the number of heads obtained:
$$ \begin{array}{c|c|c|c} \text{Heads (outcomes)} & {0} & {1} & {2} & {3} \\ \hline \text{Probability} & {1/8} & {3/8} & {3/8} & {1/8} \\ \end{array} $$
To come up with a cumulative distribution function, we have to calculate the cumulative probabilities.
The cumulative probability that X is less than or equal to zero is 1/8.
To find the cumulative probability that X is less than or equal to 1, we add P(X = 0) and (P = 1):
$$ P(X \le 1) =\cfrac {1}{8} + \cfrac {3}{8} = \cfrac {1}{2} $$
Similarly,
$$ P(X \le 2) = \cfrac {1}{8} + \cfrac {3}{8} + \cfrac {3}{8} = \cfrac {7}{8} $$
Lastly,
$$ P(X \le 3) = \cfrac {1}{8} + \cfrac {3}{8} + \cfrac {3}{8} +\cfrac {1}{8} = 1 $$
$$ \begin{array}{c|c|c|c} \text{Heads (outcomes)} & {0} & {1} & {2} & {3} \\ \hline \text{Probability} & {1/8} & {3/8} & {3/8} & {1/8} \\ \hline \text{Cumulative prob.} & {1/8} & {4/8} & {7/8} & {8/8} \\ \end{array} $$
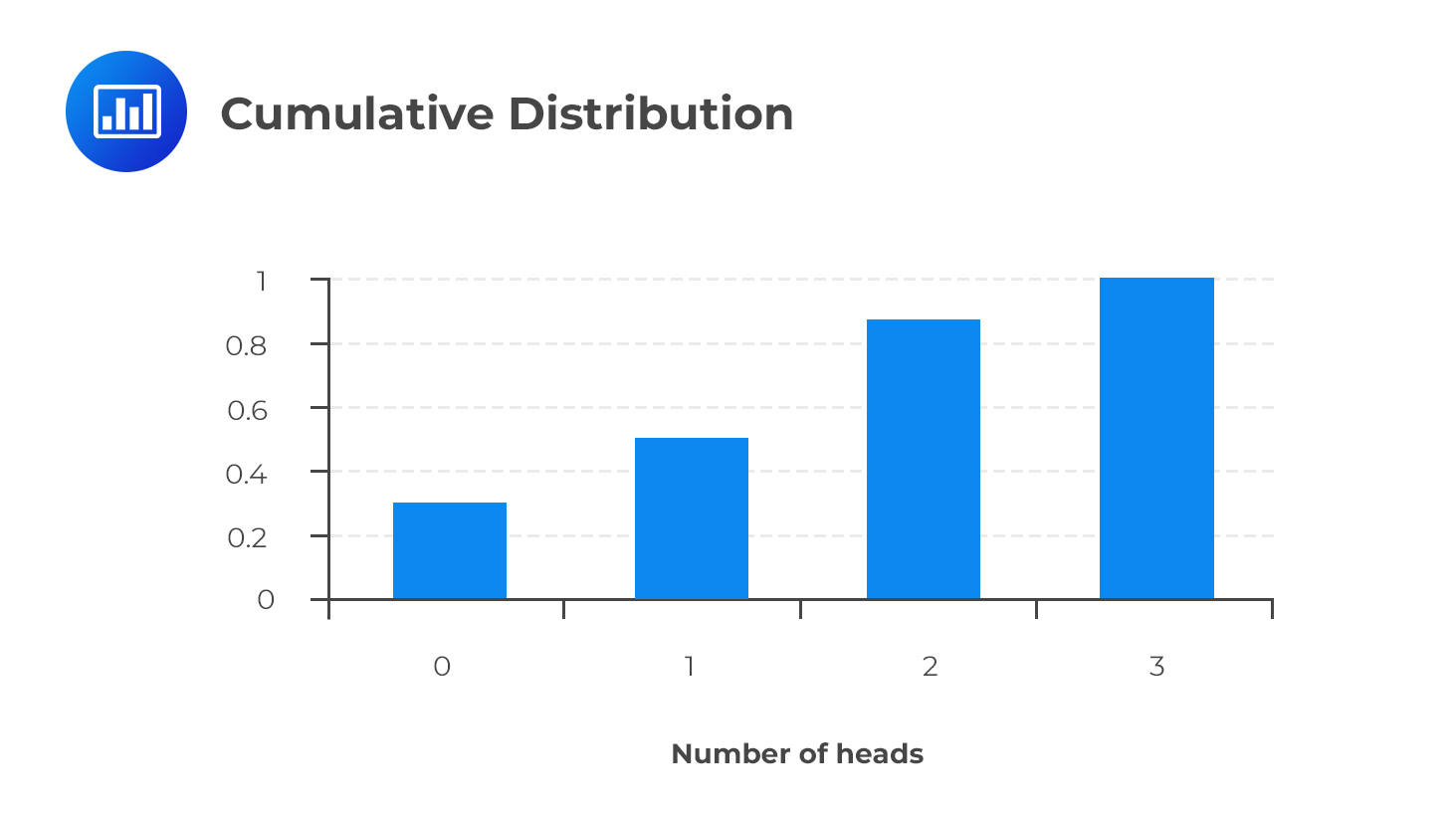
The CDF has two main properties:
A cumulative distribution function can help us to come up with cumulative probabilities pretty easily. For example, we can use it to determine the probability of getting at least two heads, at most two heads, or even more than two heads. For example, the probability of at most two heads from the cumulative distribution above is 0.875.
Question
Variable X can take the values 1, 2, 3, and 4. The probability of each outcome has been given below.
$$ \begin{array}{c|c|c|c|c} \text{Outcome} & {1} & {2} & {3} & {4} \\ \hline \text{Probability} & {0.2} & {0.3} & {0.35} & {0.15} \\ \end{array} $$
Construct a table showing the cumulative distribution and use it to determine P(X ≤ 2).
A. 0.5
B. 0.3
C. 0.85
Solution
The correct answer is A.
You simply sum up the probabilities up to and including a given outcome and come up with a table similar to the one below:
$$ \begin{array}{c|c|c|c|c} \text{Heads (outcomes)} & {1} & {2} & {3} & {4} \\ \hline \text{Probability} & {0.2} & {0.3} & {0.35} & {0.15} \\ \hline \text{Cumulative prob.} & {0.2} & {0.5} & {0.85} & {1} \\ \end{array} $$
From the table, it is clear that \(P(X \le 2) = 0.5\).
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.