Common Chart Patterns
A chart pattern is a distinct trading formation appearing repeatedly and which can... Read More
We calculate the predicted value of the dependent variable, \(Y\), by inserting the estimated value of the independent variable, \(X\), into the regression equation. The predicted value of the dependent variable, \(Y\), is determined using the following formula:
$$\hat{Y}=\hat{b}_0+\hat{b}_1X$$
Where:
\(\hat{Y}\) = Predicted value of the dependent variable.
\(X\) = Estimated value of the independent variable.
Example: Calculating the Predicted Value of a Dependent Variable
Refer to the example of regressed inflation rates against unemployment rates from 2011 to 2020.
$$ \begin{array}{c|c|c|c|c|c|c|c}
\text{Year} & \text{Unemployment} & \text{Inflation} & \text{Predicted} & \text{Variation} & \text{Variation} & \text{Variation} & (X_i \\
& {\text{Rate } \% (X_i)} & {\text{Rate }\%} & \text{Unemployment} & \text{to be} & \text{Unexplained} & \text{Explained} & -\bar{X})^2 \\
& & ({{Y}}_i) & {\text{rate } (\hat Y_i)} & \text{Explained.} & & & \\
& & & & \left(Y_i-\bar{Y}\right)^2 & \left(Y_i- \hat{Y}_i\right)^2 & \left({\hat{Y}}_i-\bar{Y}\right)^2 & \\ \hline
2011 & 6.1 & 1.7 & 1.610 & 0.410 & 0.008 & 0.533 & 0.656 \\ \hline
2012 & 7.4 & 1.2 & 0.437 & 1.300 & 0.582 & 3.621 & 4.452 \\ \hline
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \hline
2019 & 4.0 & 4.7 & 3.504 & 5.570 & 1.430 & 1.355 & 1.664 \\ \hline
2020 & 3.9 & 3.6 & 3.594 & 1.588 & 0.000 & 1.573 & 1.932 \\ \hline
\textbf{Sum} & \bf{52.90} & \bf{23.4} & & \bf{13.704} & \bf{3.136} & \bf{10.568} & \bf{12.989} \\ \hline
\textbf{Arithmetic} & \bf{5.29} & \bf{2.34} & & & & & \\
\textbf{Mean} & & & & & & & \\
\end{array} $$
The estimated regression model is illustrated below.
$$ \hat{Y}=7.112-0.9020X_i+\varepsilon_i $$
Calculate the predicted inflation rate value if the forecasted value of the unemployment rate is 4.5%.
Solution
The predicted value of the inflation rate is determined as follows:
$$ \hat{Y}=7.112-0.9020\times4.5=3.053\% $$
The confidence interval calculation for the predicted value of a dependent variable is the same as that of the confidence interval for regression coefficients. The confidence interval for a predicted value of the dependent variable is given by:
$$\text{Prediction Interval}=\ \hat{Y}\pm t_cs_f$$
Where:
\(t_c\)= Two-tailed critical t-value at the given significance level with \(n – 2\) df.
\(\hat{Y}\) = Predicted value of a dependent variable.
\(s_f^2\)= The estimated variance of the prediction error.
$$ s_f^2=s_e^2\left[1+\frac{1}{n}+\frac{\left(X_f-\bar{X}\right)^2}{\left(n-1\right)s_x^2}\right]=s_e^2\left[1+\frac{1}{n}+\frac{\left(X_f-\bar{X}\right)^2}{\sum_{i\ =\ 1}^{n}\left(X_i-\bar{X}\right)^2}\right] $$
Where:
\(s_e^2\) = The squared standard error of the estimate.
\(n\) = Number of observations.
\(s_X^2\)= Variance of the independent variable.
\(X_f\) = Value of the independent variable.
We can, therefore, calculate the standard error of forecast as shown below:
$$s_f=s_e\sqrt{1+\frac{1}{n}+\frac{\left(X_f-\bar{X}\right)^2}{\sum_{i=1}^{n}\left(X_i-\bar{X}\right)^2}}$$
From the formula above, we can observe that:
Example: Calculating the Confidence Interval of the Predicted Value
Refer to the example of regressed inflation rates against unemployment rates from 2011 to 2020.
$$ \begin{array}{c|c|c|c|c|c|c|c}
\text{Year} & \text{Unemployment} & \text{Inflation} & \text{Predicted} & \text{Variation} & \text{Variation} & \text{Variation} & (X_i \\
& {\text{Rate } \% (X_i)} & {\text{Rate }\%} & \text{Unemployment} & \text{to be} & \text{Unexplained} & \text{Explained} & -\bar{X})^2 \\
& & ({{Y}}_i) & {\text{rate } (\hat Y_i)} & \text{Explained.} & & & \\
& & & & \left(Y_i-\bar{Y}\right)^2 & \left(Y_i- \hat{Y}_i\right)^2 & \left({\hat{Y}}_i-\bar{Y}\right)^2 & \\ \hline
2011 & 6.1 & 1.7 & 1.610 & 0.410 & 0.008 & 0.533 & 0.656 \\ \hline
2012 & 7.4 & 1.2 & 0.437 & 1.300 & 0.582 & 3.621 & 4.452 \\ \hline
\vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \hline
2019 & 4.0 & 4.7 & 3.504 & 5.570 & 1.430 & 1.355 & 1.664 \\ \hline
2020 & 3.9 & 3.6 & 3.594 & 1.588 & 0.000 & 1.573 & 1.932 \\ \hline
\textbf{Sum} & \bf{52.90} & \bf{23.4} & & \bf{13.704} & \bf{3.136} & \bf{10.568} & \bf{12.989} \\ \hline
\textbf{Arithmetic} & \bf{5.29} & \bf{2.34} & & & & & \\
\textbf{Mean} & & & & & & & \\
\end{array} $$
Consider the results of the regression analysis of inflation rates on unemployment rates:
$$ \begin{array}{lcccc}
\bf{\textit{Regression Statistics} } & & & & \\ \hline
\text{R Square} & 0.7711 & & & \\
\text{Standard Error} & 0.6261 & & & \\
\text{Observations} & 10 & & & \\ \hline \\ \hline
\text{ANOVA} & & & & \\ \hline
& \textbf{df} & \textbf{Sum of} & \textbf{Mean} & \textbf{F} \\
& & \textbf{Squares} & \textbf{Square} & \\ \hline
\text{Regression} & 1 & 10.568 & 10.568 & 26.9565 \\
\text{Residual} & 8 & 3.136 & 0.392 & \\
\text{Total} & 9 & 13.704 & & \\ \hline
\\ \hline
& \textbf{Coefficients} & \textbf{Standard} & \textbf{t Stat} & \textbf{p-value} \\
& & \textbf{Error} & & \\ \hline
\text{Intercept} & 7.112 & 0.940 & 7.565 & 0.000 \\
\text{Unemployment} & -0.902 & 0.174 & -5.192 & 0.001 \\
\text{rate (%)} & & & & \\ \hline
\end{array} $$
Given that the forecasted unemployment rate is 4.5%, calculate the 95% confidence interval for the predicted inflation rate value.
Solution
$$\text{Prediction Interval} = \hat{Y} \pm t_{c}s_{f}$$
The estimated variance of the prediction error is:
$$ \begin{align*}
s_f^2 & =s_e^2\left[1+\frac{1}{n}+\frac{\left(X_f-\bar{X}\right)^2}{\left(n-1\right)s_X^2}\right] \\ & =s_e^2\left[1+\frac{1}{n}+\frac{\left(X_f-\bar{X}\right)^2}{\sum_{i=1}^{n}\left(X_i-\bar{X}\right)^2}\right] \\ & ={0.6261}^2\left[1+\frac{1}{10}+\frac{\left(4.5-5.29\right)^2}{12.989}\right]=0.450 \end{align*} $$
As such, the standard error of forecast is:
$$ s_f=\sqrt{0.450}=0.6708 $$
The predicted value of the inflation rate given an unemployment rate of 4.5% is:
$$ \hat{Y}=7.112-0.9020\times4.5=3.05\% $$
The two-tailed critical t-value with 8 \((n-2)\) degrees of freedom at the 5% significance level is 2.306.
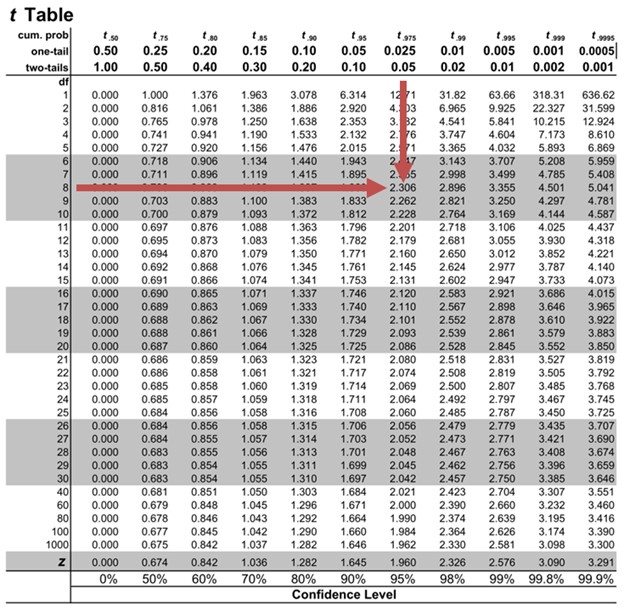
The prediction interval at the 95% confidence level is:
$$\text{Prediction Interval (PI)} = \hat{Y} \pm t_{c}s_{f}$$
$$\text{PI} = 3.05 \pm 2.306\times 0.6708= 1.50\% \text{ to } 4.60\%$$
Interpretation
Given an unemployment rate of 4.5%, we are 95% confident that the inflation rate will lie between 1.50% and 4.60%.
Question 1
The regression equation of the quantity of goods against the price is given by:
$$Y =-159+0.26X$$
Where:
\(Y\) = Quantity supplied.
\(X\) = Price per unit of the product.
The predicted value of the quantity supplied when the price equals 1,200 is closest to:
- 153.
- 155.
- 471.
The correct answer is A.
$$Y = -159 + 0.26\times1,200=153$$
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.