Chi-square and F-Distributions

Chi-square Distribution

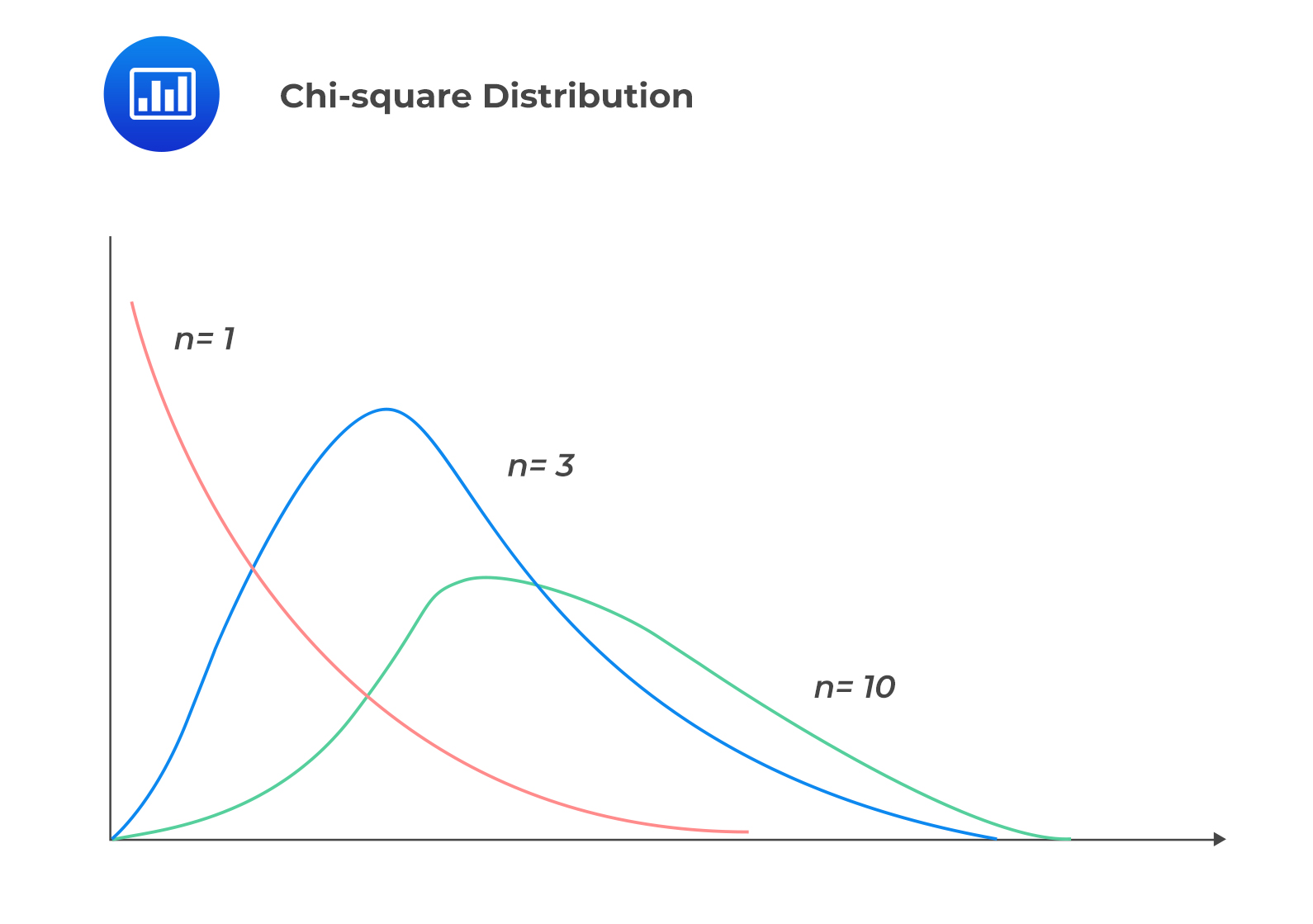
A chi-square distribution is an asymmetrical family of distributions. A chi-square distribution with \(v\) degrees of freedom is the distribution of the sum of the squares of  \(v\) independent standard normally distributed random variables. Intuitively, chi-square distributions take only non-negative random variables.

A chi-square distribution is used to test the variance of a population that is distributed normally.

In a summary, the following are the properties of a chi-square distribution:

• A chi-square distribution is a non-symmetrical distribution (skewed to the right).
• A chi-square distribution is defined by one parameter: Degrees of freedom (df), \(v = n – 1\).
• A chi-square distribution is the sum of the squares of \(k\) independent standard normally distributed random variables. Hence, it is a non-negative distribution.
• For each degree of freedom, there are different chi-square distributions.
• The shape of a chi-square distribution changes with the change in the degrees of freedom. The more the degrees of free increase, the more the distribution assumes the shape of a standard normal distribution.

F-Distribution

An F-distribution is used to test the equality of variances of two normally distributed populations from two independent random samples.

The following are the properties of an F-distribution:

• An F-distribution is an asymmetrical distribution (skewed to the right).
• An F-distribution is defined by two parameters, i.e., degrees of freedom of the numerator ( \(m\)) and degrees of freedom of the denominator ( \(n\)).
• Like a chi-square distribution, an F-distribution can only have positive values.
• As the degrees of freedom for the numerator and the denominator increase, the F-distribution approximates the normal distribution.

Relationship between the Chi-square and F-distributions

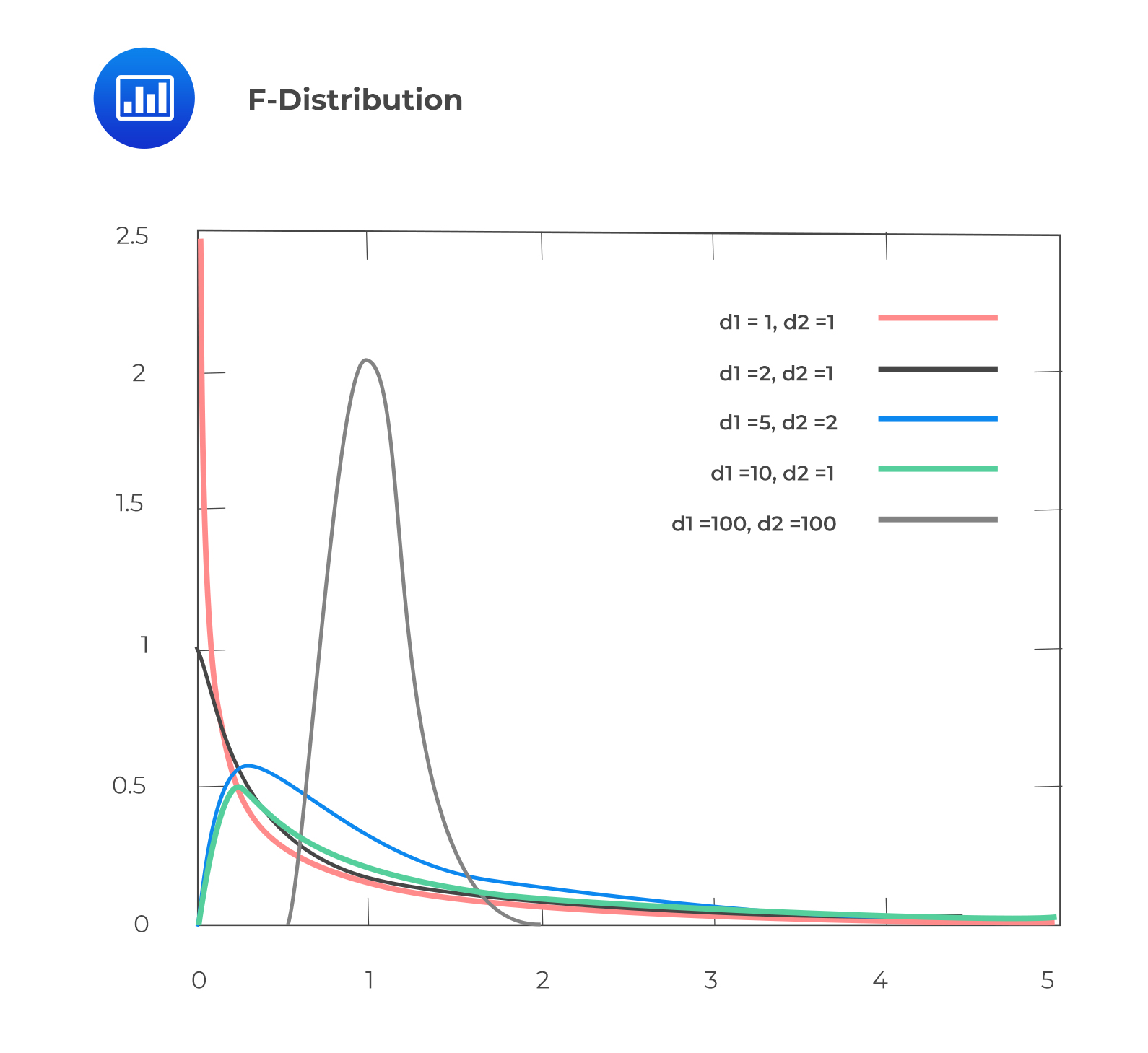
The F-distribution is the ratio of two chi-square distributions with degrees of freedom \(m\) and  \(n\), respectively, where each chi-square has first been divided by its degrees of freedom, i.e.,

$$
F=\frac{\left(\frac{\chi_{1}^{2}}{m}\right)}{\left(\frac{\chi_{2}^{2}}{n}\right)}
$$

Where  \(m\) is the numerator degrees of freedom and  \(n\) is the denominator degrees of freedom.

Question

Which of the following are most likely common characteristics of F-distribution and chi-square distribution?

1. Both can take only positive value.
2. Both are defined by two parameters.
3. Both are negatively skewed distributions.

Solution

The correct answer is A.

Both F-distribution and chi-square distribution can only take non-negative values.

B is incorrect. A chi-square distribution is defined by one parameter (i.e., n-1 degrees of freedom), while an F-distribution is defined by parameters, i.e., degrees of freedom of the numerator (m) and degrees of freedom of the denominator (n).

C is incorrect. Both the F-distribution and the chi-square distribution are positively skewed distributions.