Correlation in CFA Level 1 (With Examples)

Covariance

Covariance is a measure of how two variables move together. The sample covariance of X and Y is calculated as follows:

$$
\mathrm{S}_{\mathrm{XY}}=\frac{\sum_{\mathrm{i}=1}^{\mathrm{N}}\left(\mathrm{X}_{\mathrm{i}}-\overline{\mathrm{X}}\right)\left(\mathrm{Y}_{\mathrm{i}}-\overline{\mathrm{Y}}\right)}{\mathrm{n}-1}
$$

A major drawback of covariance is that it is difficult to interpret since its value can vary from negative infinity to positive infinity.

What is Correlation?

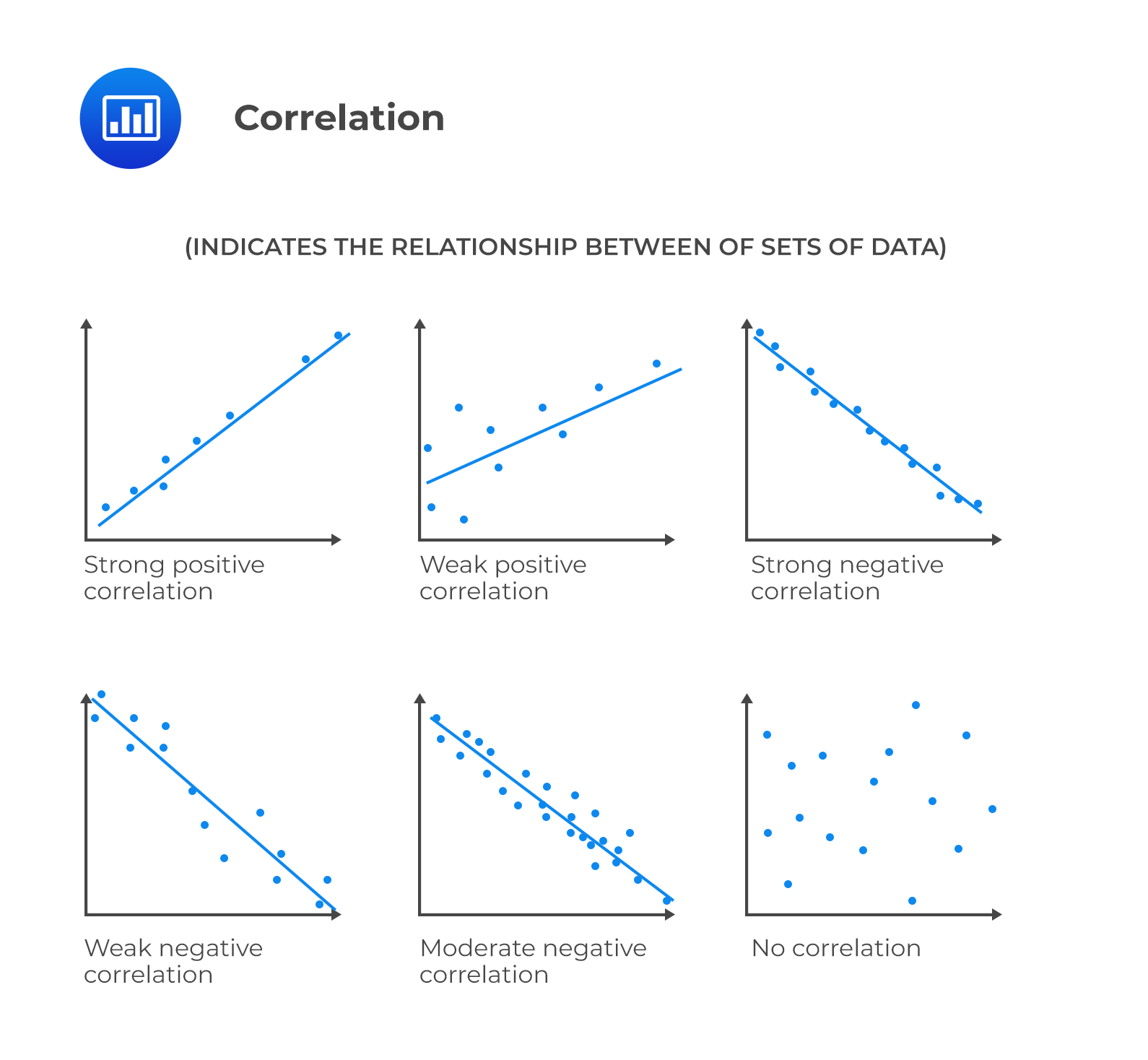
Correlation is a measure of the linear relationship between two variables. It takes the covariance and divides it by the product of the standard deviations of both variables. As a result, its value ranges between -1 and +1 and is easier to interpret.

The sample correlation coefficient is calculated as follows:

$$ r_{X Y}=\frac{s_{X Y}}{s_{x} \times s_{y}} $$

Where:

\(s_{X Y}\) = Covariance between variable X and Y.

\(s_{X}\) = Standard deviation of variable X.

\(s_{Y}\) = Standard deviation of variable Y.

Properties of Correlation

• Correlation ranges between −1 to +1 for two random variables, X and Y.
• A correlation of 0 (uncorrelated variables) indicates no linear (straight line) relationship exists between the variables.
• A positive correlation close to +1 indicates a strong positive linear relationship.
• A correlation of 1 indicates a perfect linear relationship.
• A negative correlation close to −1 indicates a strong negative linear relationship.
• A correlation of −1 indicates a perfect inverse linear relationship.

Limitations of Correlation Analysis

• Two variables can have a very low correlation despite having a strong nonlinear relationship.
• Correlation can be an unreliable measure when outliers are present in the data.
• Correlation does not imply causation. This implies that correlation may be spurious. A spurious correlation refers to:
  • correlation between two variables due to chance relationships in a particular dataset;
  • correlation arising between variables when they are divided by a third variable; or
  • correlation between two variables arising from their relation to a third variable.

Question

The correlation coefficient between X and Y is 0.7 and the covariance is 29. If the variance of Y is 25, the variance of X is closest to:

1. 8.29.
2. 29.
3. 68.65.

Solution

The correct answer is C.

$$\begin{align} r_{X Y} &=\frac{s_{X Y}}{s_{X} \times S_{Y}}\\ \Rightarrow 0.7 &=\frac{29}{X \bullet 5} \\ \therefore X&=8.2857\\ \\ \text{Variance} &=8.2857^2=68.65 \end{align}$$