Discrete Uniform Random Variables, a B ...
Probability distributions have different shapes and characteristics. As such, we describe a... Read More
Kurtosis refers to the measurement of the degree to which a given distribution is more or less ‘peaked’ relative to the normal distribution. The concept of kurtosis is very useful in decision-making. In this regard, we have 3 categories of distributions:
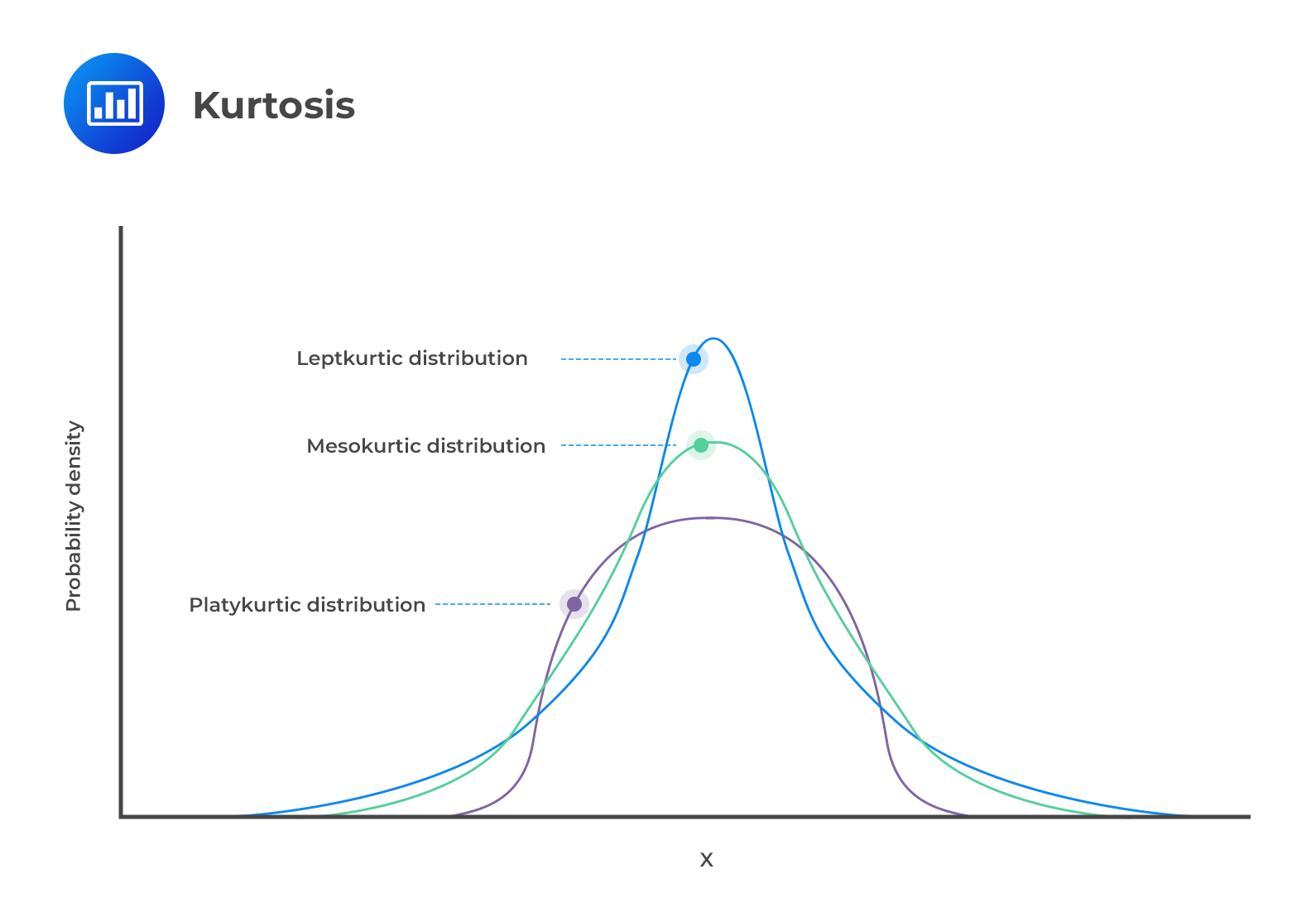
A leptokurtic distribution is more peaked than the normal distribution. The higher peak results from the clustering of data points along the x-axis. The tails are also fatter than those of a normal distribution. The coefficient of kurtosis is usually more than 3.
The term “lepto” means thin or skinny. When analyzing historical returns, a leptokurtic distribution means that small changes are less frequent since historical values are clustered around the mean. However, there are also large fluctuations represented by the fat tails.
A platykurtic distribution has extremely dispersed points along the x-axis, resulting in a lower peak when compared to a normal distribution. “Platy” means broad. Hence, the prefix fits the distribution’s shape, which is wide and flat. The points are less clustered around the mean compared to a leptokurtic distribution. The coefficient of kurtosis is usually less than 3.
Returns that follow this type of distribution have fewer major fluctuations compared to leptokurtic returns. However, you should note that fluctuations represent the riskiness of an asset. More fluctuations represent more risk and vice versa. Therefore, platykurtic returns are less risky than leptokurtic returns.
Lastly, mesokurtic distributions have a curve that is similar to that of a normal distribution. In other words, the distribution is largely normal.
Exam tip: The learning outcome statement reads, “explain measures of sample skewness and kurtosis.” However, the calculations will have you better understand those concepts.
$${ S }_{ k }=\frac { 1 }{ n } \frac { \sum _{ i=1 }^{ n }{ { \left( { X }_{ i }-\bar { X } \right) }^{ 3 } } }{ { S }^{ 3 } } $$
Where:
\(\bar { X }\) = Sample mean;
\(S\) = Sample standard deviation; and
\(n\) = Number of observations.
Note: The formula is very similar to the formula for standard deviation, but raised to the 3rd power.
Interpretation: A positive value indicates positive skewness. A ‘zero’ value indicates that the data is not skewed. Lastly, a negative value indicates negative skewness or rather a negatively skewed distribution.
Sample kurtosis is always measured relative to the kurtosis of a normal distribution, which is 3. Therefore, we are always interested in the “excess“ kurtosis, i.e.,
\(\text{ Excess kurtosis = Sample kurtosis – 3 }\), where:
\({ S }_{ kr }=\frac { 1 }{ n } \frac { \sum _{ i=1 }^{ n }{ { \left( { X }_{ i }-\bar { X } \right) }^{ 4 } } }{ { S }^{ 4 } } \)
Interpretation: Positive excess kurtosis indicates a leptokurtic distribution. A zero value indicates a mesokurtic distribution. Lastly, a negative excess kurtosis represents a platykurtic distribution.
Suppose we have the following observations:
{ 12 13 54 56 25 }
What is the skewness of the data?
Solution
First, we must determine the sample mean and the sample standard deviation:
$$ X =\cfrac {(12 + 13 +…+25)}{5} =\cfrac {160}{5} = 32 $$
$$ S^2= \cfrac{{(12 – 32)^2 + …+ (25 – 32)^2}}{4} = 467.5 $$
Therefore,
$$ S = 467.5^{\frac{1}{2}} = 21.62 $$
Now we can work out the skewness:
$${ S }_{ k }=\frac { 1 }{ n } \frac { \sum _{ i=1 }^{ n }{ { \left( { X }_{ i }-\bar { X } \right) }^{ 3 } } }{ { S }^{ 3 } } =\frac { 1 }{ 5 } \frac { { -20 }^{ 3 }+{ (-19 }^{ 3 })+{ 22 }^{ 3 }+{ 24 }^{ 3 }+{ (-7 }^{ 3 }) }{ { 21.62 }^{ 3 } } =0.1835 $$
Skewness is positive. Hence, the data has a positively skewed distribution.
Using the data from the example above { 12 13 54 56 25 }, determine the type of kurtosis present.
Solution
$$ X =\cfrac {(12 + 13 +…+25)}{5} =\cfrac {160}{5} = 32 $$
$$ S^2=\cfrac {{(12 – 32)^2 + …+ (25 – 32)^2}}{4} = 467.5 $$
Therefore,
$$ S = 467.5^{\frac{1}{2}} = 21.62 $$
\({ S }_{ kr }=\frac { 1 }{ n } \frac { \sum _{ i=1 }^{ n }{ { \left( { X }_{ i }-\bar { X } \right) }^{ 4 } } }{ { S }^{ 4 } } =\frac { 1 }{ 5 } \frac { { -20 }^{ 4 }+{ (-19 }^{ 4 })+{ 22 }^{ 4 }+{ 24 }^{ 4 }+{ (-7 }^{ 4 }) }{ { 21.62 }^{ 4 } } =0.7861\)
Next, we subtract 3 from the sample kurtosis and get the excess kurtosis:
\(\text {Excess kurtosis} = 0.7861 – 3 = -2.2139\)
Since the excess kurtosis is negative, we have a platykurtic distribution.
Question 1
The skewness of the normal distribution is most likely:
- zero.
- positive.
- negative.
Solution
The correct answer is A.
Since the normal curve is symmetric about its mean, its skewness is zero.
B is incorrect because a positively skewed distribution has positive skewness.
C is incorrect because a negatively skewed distribution has negative skewness.
Question 2
A frequency distribution in which there are too few scores at the extremes of the distribution is most likely called:
- platykurtic.
- leptokurtic.
- mesokurtic.
Solution
The correct answer is A.
A platykurtic distribution has “thin” tails and is flatter compared to a normal distribution. It implies that there are fewer scores at the extremes of the distribution, which aligns with the question’s description.
Question 3
When most of the data are concentrated on the left of the distribution, it is most likely called:
- symmetric distribution.
- positively skewed distribution.
- negatively skewed distribution.
Solution
The correct answer is B.
A distribution is said to be skewed to the right, or positively skewed, when most of the data are concentrated on the left of the distribution. A distribution is said to be skewed to the left, or negatively skewed, if most of the data are concentrated on the right of the distribution. The left tail clearly extends farther from the distribution’s center than the right tail.
A is incorrect. A symmetric distribution is one in which the left and right sides mirror each other.
C is incorrect. A distribution is said to be skewed to the left, or negatively skewed, if most of the data are concentrated on the right of the distribution. The left tail extends farther away from the mean than the right tail.
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.