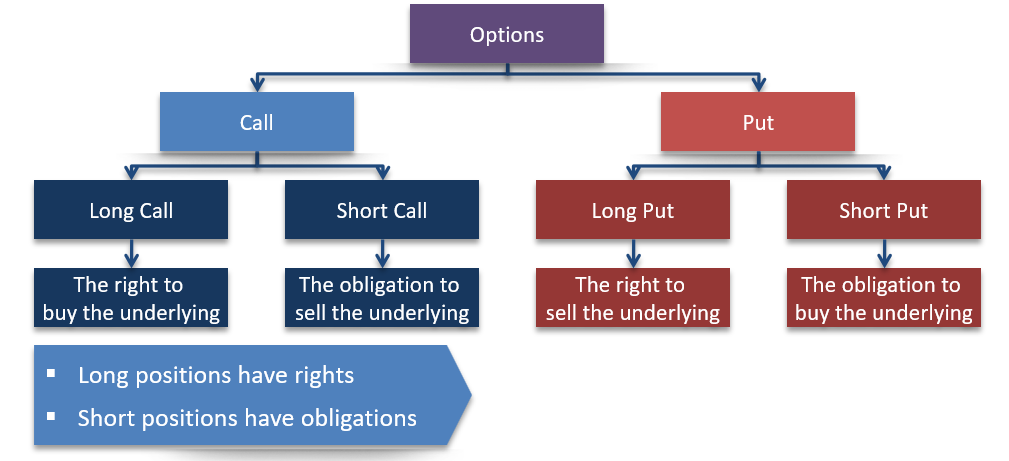
The buyer of an option has the right but not the obligation to exercise the option. The maximum loss to the buyer is equal to the premium paid for the option. The potential gains are theoretically infinite. To the seller (writer), however, the maximum gain is limited to the premium received after writing the option. The potential loss is unlimited.

In an options contract, two parties transact simultaneously. The buyer of a call or a put option is the long position in the contract while the seller of the option, also known as the writer of the option, is the short position.

Call Options

Value at Expiration of a Call Option

The payoff for a call buyer at expiration date T is given by \(max(0,S_T–X)\) while the payoff for a call seller is \(-max(0,S_T–X)\).

Where:

\(S_T\) is the price of the underlying at expiration; and

X is the exercise price.

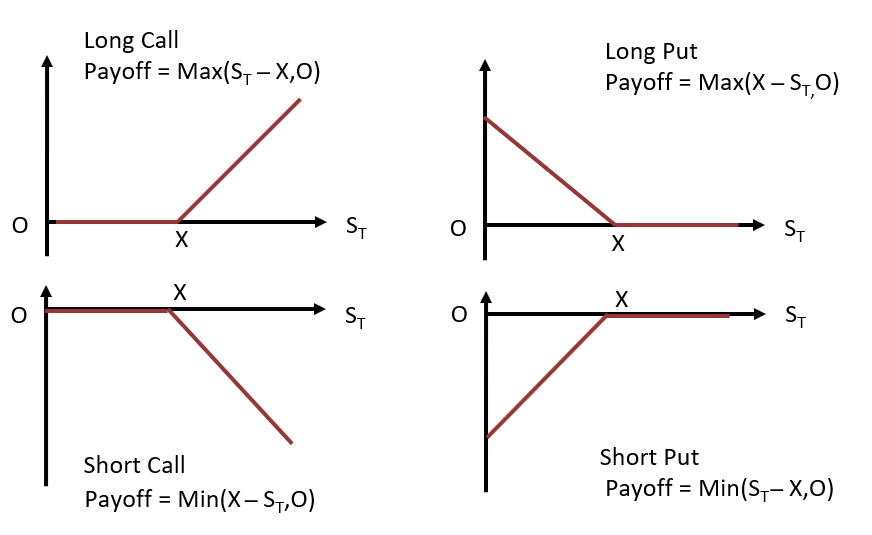
Using the payoff profile and the price paid for the option, the profit equation of a call option can be written as follows:

Call buyer

Payoff for a call buyer \(=max(0, S_T-X)\)

Profit for a call buyer \(=max(0, S_T–X)-c_0\)

Call seller

Payoff for a put seller \(=-max(0,S_T–X)\)

Profit for a call seller \(=-max(0, S_T–X)+c_0\)

where \(c_0\) the call premium.

The buyer of the call option has no upper limit on the potential profit and a fixed downside loss equal to the premium. The seller, on the other hand, has unlimited losses and a gain limited to the premium:

Long Call

The profit from buying one European call option: Option price = $10, Strike price = $200 can be shown as follows:

Short Call

The profit from writing one European call option: Option price = $10, Strike price = $200 is shown below:

Put Options

By now, if you have well understood the basic characteristics of call options, then the payoff and profit for put option buyers and sellers should be quite easy; simply replace \( “S_T-X” \text{ by } “X-S_T” \).

https://analystprep.com/shop/cfa-unlimited-package-for-level-1-2-3/

Value at Expiration of a Put Option

The payoff and profit profiles of a put option are represented as follows:

Put buyer

Payoff for a put buyer \(=max(0,X-S_T)\)

Profit for a put buyer \(=max(0,X-S_T)-p_0\)

Put seller

Payoff for a put seller \(=-max(0,X-S_T)\)

Profit for a put seller \(=-max(0,X-S_T)+p_0\)

Where \(p_0\) is the put premium.

The put buyer has a limited loss and, while not completely unlimited gains, as the price of the underlying cannot fall below zero, the put buyer does gain as the price falls. As such, purchasing a put option is like purchasing insurance. In the same vein as for call options, the put seller has nearly unlimited losses, and his gains are limited to the put premium paid to him by the put buyer.

Long Put

The profit from buying a European put option: Option price = $14, Strike price = $140.

Short Put

The profit from writing a European put option: Option price = $14, Strike price = $140.

Example: Option Payoff

At expiration, the underlying asset price \( S_T\) is $29. If the strike price X is $26, what is the payoff to the put and call buyers?

Solution

The payoff to the call buyer:

\(c_T=\ max(0,S_T\ – X) = max(0,$29 – $26) = $3\)

The payoff to the put buyer: 

\(p_T=\ max(0,X\ – S_T) = max(0,$26 – $29) = 0\)

When the option has a positive payoff, it is said to be in the money. In the example above, the call option is in the money. The put option is out of the money because \(X\ – S_T\) is less than 0. When \(S_T\ =\ X\), the option is said to be at the money.

Example: Option Value

Assume that a put and call on XYZ stock have the same strike price of X = $35. The call initially costs $2, and the put costs $3.

What is the profit on the long call and long put if the price of CBX stock at expiration \(S_T\) is $28?

Solution

Profit to the call buyer \(=max(0,S_T–X)-c_0=max(0,$28 – $35) – $2 = – $2 \)

Profit to the put buyer \(=\ max(0,X\ – S_T) – p_0 = max(0,$35 – $28) – $3 = $4\)

Expiration and Strike Price

Expiration

Exchange-traded stock options can either be American or European style. While European options can only be exercised at expiry, American options can be exercised at any point during the life of the option. The exchange specifies the actual date of expiry.

Strike Prices

Тhe value of the stock directly controls the strike price. At the expiration date, the difference between the stock’s market price and the option’s strike price determines the payoff.

Moneyness

Call Options:

• If the stock price exceeds the exercise price, the option is in-the-money (ITM).
• If the stock price is less than the exercise price, the option is out-of-the-money (OTM).
• If the current market price is equal to the strike price, the option is at-the-money (ATM).

Put Options:

• If the stock price is less than the exercise price, the option is in-the-money (ITM).
• If the stock price exceeds the exercise price, the option is out-of-the-money (OTM).
• If the current market price is equal to the strike price, the option is at-the-money (ATM).

Examples: Moneyness of a call option

A stock has a current price of $100. The exercise price of a call option is $105.

Is the option in-the-money, at the money, or out of the money?

Solution

The call option is out of the money (OTM) since the stock price is less than the exercise price. The option would be in the money anywhere above the exercise price of $105.

Examples: Moneyness of a put option

A stock has a current price of $50. The exercise price of a put option is $45.

Is the option in-the-money, at the money, or out of the money?

Solution

The put option is out of the money (OTM) since the stock price exceeds the exercise price. The option would be in the money anywhere below the exercise price of $45.

Intrinsic Value and Time Value

The intrinsic value of an option is the difference between the prevailing market price of the underlying security and the strike price.

Call option 

The intrinsic value of a call option is the \(max(0,\ S_T-\ X)\).

Put option

The intrinsic value of a put option is the \( max(0,\ X\ -S_T)\).

The time value of an option is the difference between the option premium and the intrinsic value.

\(Option\ premium\ =\ Intrinsic\ value+\ Time\ value\)

Example: Value at expiration

Consider a put option with a premium of $11, and the exercise price is $129. The price of the underlying security is $123. What are the value at expiration and the gain/loss to that put option buyer?

Solution

The exercise price is greater than the underlying price, i.e., $123 > $129.

Therefore the payoff \(p_T=0\) and \(profit=0-11=-11\).

Value at expiration = $0

Loss to the put buyer = $11