GMAT Problem Solving: Technical Mathematics

While there are several ways of solving mathematical problems in the quantitative reasoning section of the GMAT, a time comes when the only reasonable tactic is technical mathematics. If you see a clearly technical math problem where no information is obscured behind opaque words, then technical math may be your only option. However, it is only going to require arithmetic, algebraic and geometric skills. The level of math on this test does not go beyond basic algebra II, which is really low in quadratic. Unfortunately, the GMAT does not necessarily associate technical mathematics with high-difficulty problems. You are not necessarily rewarded for completing some of the arithmetic or geometric technical math that you may consider difficult to do, especially at the beginning of your preparation. 

What are the strategic Implications of technical math in the Exam?

Always try the technical approach first because if you can do it, it’s probably the fastest. However, you must have a tight leash on this approach because as soon as it ceases to be both apparent and simple, you must abandon it quickly to keep up your pace.

• Apparent- If it is apparent, it means you can set up the math. Arithmetic is usually there implicitly. You need to ask yourself, “Can I create the algebra?” Or,” Can I construct the geometry?” If your answer to these questions is “Yes.” Then it is apparent. 
• Simple- This means you can solve the math with ease. Sometimes you may be given a problem, and although it is apparent, it is simple for you.

Note the numbering format in your question and choices to inform efficient calculations. For instance, do your calculations in fractions if your answer choices are in fractions and in decimals if your answer choices are in decimals. Make sure that you are math ambidextrous so that you don’t force yourself into a situation where you have to use a single specific number format for non-integer valuation all the time.

Technical Mathematics Problem Solving Process

Word Problem Example

If Abby travels 4miles in minutes, and Barry travels 2miles in b minutes, which of the following represents the number of minutes it would take Callum to travel 10 miles at the average of Abby’s and Barry’s rates in terms of a and b?

1. \(\frac{2a+b}{10ab}\)
2. \(\frac{2b+a}{10ab}\)
3. \(2b+a\)
4. \(\frac{10ab}{2a+b}\)
5. \(\frac{10ab}{2b+a}\)

Problem Solving process

1. You will need to set up your scratch pad by listing the choices A through E. 
2. Skip to the end of the problem and identify what is sought, then label your choices as such. # no. Of minutes for c to travel 10 miles=?
3. Read from the beginning, taking notes and setting up equations as you go. From the answer choices, you can tell that your answer should be an algebraic expression.

We can start with the formula: \(\text{rate}=\frac{\text{distance}}{\text{Time}}/ \text{time}=\frac{\text{distance}}{\text{rate}}\)

• Average rate: =\(\frac{4/a+2/b}{2}\)
• Process fraction: =\(\frac{4a+2b}{2ab}\)
• Simplify fraction: =\(\frac{2a+b}{ab}\)
• Solve for times as t: = \(\frac{10}{\frac{2a+b}{ab}}\)
• Multiply by reciprocal, \(t=\frac{10ab}{2a+b}\)

This matches choice E.

Remember that this needs to be both apparent and simple to you at the moment. If ever you get stuck while working through a word problem,  there may be an alternative approach that you can explore, but as you can see, it’s probably the fastest if you follow this technical approach.

Arithmetic Example

Square root of \(((27)(10) – (9)(15))\)

1. \(3\sqrt{5}\)
2. 5
3. 10
4. \(10\sqrt{3}\)
5. 15

Process

You will need to set up your scratch pad by listing the choices A through E. Include simple numbers. 

Note the format of choices to facilitate efficient manipulation. You cannot do an approximation in this case, you have to solve technically until you get the final answer. From the choice, you can see that we can have the answer in square root form. This will inform our approach, we have to remove common factors to simplify these roots.  

• Ignoring the root sign \(27\times10-9\times5\)
• 9 is a common factor \(9(3\times10-1\times5)\)
• Process parentheses \(9(30-5)=9\times25\)
• Put the radical back \(\sqrt(9\times25)=3\times5=15\)
• Distribute radical \(3\times5=15\)

There is no alternative approach to solving this problem. You have to use technical math, if you can’t find a way forward in this kind of arithmetic problem,  your best alternative is to make a guess and move on quickly.

Geometric Example

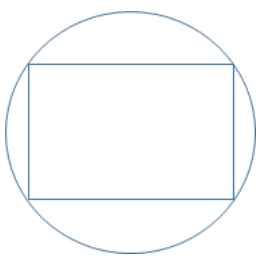
If the diameter of the circle above is 10, what is the area of the rectangle inscribed in the circle?

1. 20
2. 40
3. 48
4. 50
5. 60

Process

You will need to set up your scratch pad by listing the choices A through E, including simple numbers. There is no need to draw the figure on your scratchpad.

Skip to the end of the problem and identify the value (s) sought.

Write down formulas and avoid drawing as much as possible

Area of rectangle = lw

 Diameter = diagonal = 10

By Pythagoras theorem, diagonal² = l² + w²

                    Area of rectangle = lw

                     Diameter = diagonal = 10

                     By Pythagoras theorem, diagonal² = l² + w²

                     Pythagorean integers = 6 : 8 : 10

                        l = 6, w = 8, d = 10

                       Area of rectangle = 6 × 8 = 48

Therefore, for technical mathematics,  our problem-solving process will be: 

Step 1

Set up a scratch pad listing your choices vertically A through E

• Note specific algebraic expressions or numbers in the choices 
• Note format of choices to inform tactics and calculations 

Step 2

Skip to the end of the problem and label choices as sought value(s)

• Note if you are seeking specific or non-specific value
• Don’t auto-solve for individual values if you are seeking combined values.

Step 3

Read from the beginning, take notes, and do the necessary calculations to maximize your efficiency. 

• If you can, take the technical math approach to solve the problem. 
• Abandon it quickly if, at any moment, it ceases to be both apparent and simple.

Sample Problem Solving question

If xy ≠ 0 and 3x² are 60 percent of 20 percent of y³, the value of y³ is how many times the value of x²? 

1. 3
2. 5
3. 10
4. 12
5. 25

Solution

Set up your scratch pad by listing the choices A through E. Skip to the end of the problem and identify what is sought, then label your choices as such(y³ is how many times the value of x²)

If \(\text{xy}≠0\)

$$(3x^{2}=0.6\times0.2\times{y}^{3})100$$

$$300x^2=6\times2\times{y}^3$$

$$(300x^2=12y^3)/12$$

$$25x^2=y^3$$

The correct answer is 25, choice E.

In this problem, the technical approach is relatively direct and expedient. You could plug in or take other alternative approaches here. But if you follow common constructs of algebra and simplification, you can reach the answer under the two-minute average per question allocated for the quantitative section.

Many GMAT test takers may shy away from technical math, however, as demonstrated above, sometimes it is the most efficient way to solve mathematical problems on the GMAT. At times, it is the only way. During your preparation for the exam, do some practice on technical math. keep it simple, and it may just save you some crucial seconds during your exam.

Best of luck as you prepare and, eventually, as you take your GMAT exam. Remember to take advantage of the GMAT study resources available on our website to prepare adequately for your exams. Practice makes perfect.