Financial Models

A “financial model” can be a lot of things. The phrase is usually used to describe a representation of a real financial situation. Financial models typically use a set of assumptions and inputs to generate an output or set of outputs that informs the user. Models can range from simple math calculations in Microsoft Excel to complex programs built using C++, Python, MATLAB, or other applications. Despite the limited capabilities and speed of Excel, it is a very common tool used in financial modeling due to its flexibility and accessibility. In this post, I will give a brief introduction to just a few types of models used in the finance industry.  Since firms and analysts have specific preferences and data sets, there is no simple instruction manual to building any type of financial model. Additionally, this is by no means an exhaustive list of all the various types of financial models being used in the world today but is simply meant to give readers a glimpse into how financial data can be used to help inform decision makers.

Valuation Models

This category encompasses a wide variety of models that ultimately use data to determine the present value and/or the expected return of an asset based on the amount and timing of estimated cash flows. Valuation models include discounted cash flow models, discounted dividend models, sum-of-the-parts models, comparable company models, and many others (major categories of equity valuation models). A key assumption in these models is usually the discount rate, which is used to roll back future cash flows into a present valuation. Some basic models may simply use an average ratio (P/E, P/B, P/CF, etc.) based on similar companies to calculate a current valuation. Valuation models may project a certain date at which the asset is expected to be sold or may calculate terminal values assuming a constant growth rate and discount rate.

Private equity fund managers generally build relatively short-term models because all portfolio company investments will be sold within a limited timeframe. Since buyout managers usually attempt to make significant changes to acquired companies, extensive adjustments to historical financial data are often required. Data-intensive models are sometimes of limited use to venture capital fund managers because potential investments usually have a very limited track record and may operate in a very young industry. Private real estate fund managers usually build projections assuming an even shorter holding period for potential property investments than private equity funds do with prospective company investments. Property valuations are often based on current capitalization rates (“cap rates”), expected occupancy rates, the cost of improvements and ongoing maintenance, the cost of debt, and projected cap rates at exit among many other factors.

Valuation models may include various sets of assumptions that can easily be compared. Analysts commonly build at least three sets of assumptions: a downside case, an upside case, and a base case to account for various uncertainties. Getting an idea of the range of possibilities of a prospective investment may help analysts overcome biases related to focusing on only the positive or negative aspects.

Monte Carlo Simulations

Monte Carlo simulations broadly describe computational algorithms that are based on running many random samples as inputs and recording the outputs. While analysts may come up with a handful of “cases” in valuation models, Monte Carlo simulations may be based on millions or even billions of random samples. These simulations can help people get an idea for the worst case, best case, average or most common scenarios. The random sampling may also help reveal certain threats or opportunities.

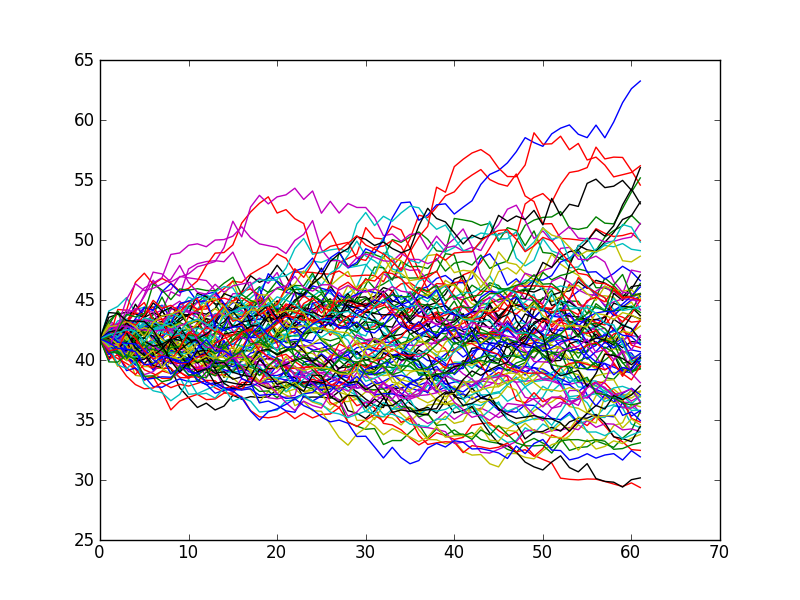
Monte Carlo simulations are used in a wide range of disciplines and are extensively used in the financial field. They are frequently used to project the performance of a portfolio of assets, whether for a pension fund, mutual fund, or individual investor’s portfolio. The well-known “Trinity Study” utilized Monte Carlo simulations using historical market data to estimate the 4% safe withdrawal rate, or the rate at which retirees could draw from their portfolio each year and be very unlikely to deplete their savings. Monte Carlo simulations may also be used to evaluate the performance of a business unit, price options, or analyze default risk.

Optimization

While Monte Carlo simulations can be extremely useful for finding a “good enough” answer to highly complex and uncertain problems, optimization aims to provide the “best” answer. The “Efficient Frontier”, developed by Harry Markowitz, tracks the point at which return is maximized for a given level of risk. Given a set of assumptions, including asset return, asset risk (standard deviation), and correlation among assets, an investor can find the optimal asset allocation to maximize his or her returns at a targeted risk level. Of course, the expected optimal asset allocation won’t be the actual optimal asset allocation as the assumptions won’t match up perfectly with reality (and are oftentimes significantly off the mark).

Optimization models are commonly used by businesses to determine the best set of decisions given a targeted goal and set of constraints. Businesses are not only limited by their budgets, but also by the employee hours, physical space, energy usage, and many other factors. The best answer in these instances is not usually obvious, but instead a combination of decisions that allocate the available resources most effectively. Excel’s data solver tool can be very helpful in solving optimization problems of limited complexity.

Pacing Models

Pacing models generally refer to models that project the future cash flows and value of a private markets portfolio in relation to a broader portfolio of assets. These models are not very well-known outside the institutional investment world. While most public market investments are valued daily and traded frequently, private market investments are much more difficult to value and trade. This poses a problem to pension funds, endowments, sovereign wealth funds, insurance companies, and other large investment entities that want to benefit from the higher expected return of private markets assets, but also wish to keep their exposure to those assets within a certain range (e.g. 10-15% of overall portfolio). Rebalancing to target asset allocations is easy and cheap to do with a portfolio of highly liquid securities so the average investor has no need to “pace” their own investments.

In the case of closed-end private markets investments, sales of partnership shares often take place at a significant discount and it can be costly to find a buyer. Due to these difficulties, it is often not ideal for investors to reduce exposure through secondary market sales and so they are typically locked into the commitments they make. Another problem is that the investor doesn’t control the timing or amount of cash flows, but instead invests money when the partnership “calls” capital and receives its money back through distributions with very limited notice. Therefore, it is useful for these large investors to project future cash flows and values so that they aren’t stuck with an allocation above or below their target.

Pacing models generally use different assumptions for the different private markets asset classes, including buyouts, venture capital, private debt, natural resources, and infrastructure. Different assumptions may also be used for the various fund strategies within each asset class. These assumptions usually include an initial contribution rate (as a % of total commitments), an ongoing contribution rate, a distribution bow (determining how the fund’s value is distributed over the course of its life), an expected return, and the expected lifespan of a fund.

Garbage In, Garbage Out (GIGO)

“GIGO” is commonly used to describe situations in which faulty inputs lead to incorrect outputs. The value of a financial model is only as good as the quality of its inputs/assumptions. While many financial analysts will use financial models on a frequent basis, it’s important to be aware of its many shortcomings. There are some instances in which projections can be reasonably assumed to line up well with what happens in reality, but this is usually not the case. Many criticize the overreliance on quantitative models in finance, along with the use of standard deviation as a risk measure (which serves as the basis of many risk models). While models can be extremely useful in visualizing what the future may hold, it usually works best to use modeling as just one of many tools and not as your entire toolkit.

As John Maynard Keynes said: “it is better to be roughly right than precisely wrong.”

All 3 Levels of the CFA Exam – Complete Course offered by AnalystPrep