Test for Differences Between Means: Paired Data

When testing for the difference between two population means, independent samples may introduce some caveats. The real difference can be masked by variability within each sample caused by factors other than those of interest to the researcher. Random variation within a sample can be so large that it blurs the real difference – that which has been caused by a phenomenon or factor in which an analyst is interested. For this reason, a paired data test may be preferred.

As a way of controlling the external variability, data analysts often collect a pair of responses from each subject. They then compute and work with the differences within pairs.

Example 1: Paired Data Test

A group of financial analysts wishes to determine whether the payment of dividends has a significant effect on the share price. Sample data on share prices can be collected from a set of companies prior to the payment of dividends, say, 7 days before dividend announcements. To ensure the samples are independent, the companies should be in the same line of business. This would ensure that all of them are susceptible to similar specific risks and other business-related conditions. Seven days after all the companies have paid the dividends, the analysts can recollect data from each company. The analysts would end up with paired data from each company. Such data can then be used to establish if any significant differences exist between pre-dividend and post-dividend share prices.

The overriding assumption during paired data tests is that the observed differences constitute a sample from a normal distribution.

Basic Situation

H₀: μ_D (= μ₁ – μ₂) = σ

The test statistic is

$$ \frac { \bar { D } -\sigma }{ \frac { { S }_{ D } }{ \sqrt { n } } } \sim { t }_{ n-1 } \text{ under } { H }_{ 0 } $$

In case n is large, the normal distribution assumption is not necessary.

Example 2: Paired Data Test

Doctors in a certain general hospital wish to determine if a special diet can reduce body weight. To do this, they select ten overweight patients with an average body weight of 77 kg (B’). After being subjected to the special diet, the average weight reduces to 75 kg (A’).

Test whether the special diet reduces body weight.

Additional information: \( \sum (B_i – A_i)^2 = 70 \quad \quad i = 1, 2, 3, …, 9, 10.\)

Solution

As always, begin by stating the hypothesis:

H₀: μ_A = μ_B

H₁: μ_A < μ_B

Where A stands for “after” and B is “before.”

The test statistic is:

$$ \frac { \bar { D } -\sigma }{ \frac { { S }_{ D } }{ \sqrt { n } } } \sim { t }_{ n-1 }\quad under\quad { H }_{ 0 } $$

Where D_i is the difference within each pair (A_i – B_i).

$$ \begin{align*} D’ & = A’ – B’ = 75 – 77 = -2 \\ S_D^2 & =\cfrac {1}{(n – 1)} \left( \sum D_i – D’ \right)^2 =\cfrac {1}{(n – 1)} \left\{ \sum D_i^2 – {nD’}^2 \right\} \\ & =\cfrac {1}{9} \left\{ 70 – 10(-2^2) \right\} = 3.333 = 1.826^2 \end{align*} $$

Therefore,

$$ \text{Test statistic} =\cfrac {(75 – 77)}{\left( \frac {1.826}{\sqrt{10}} \right)} = -3.591 $$

The test statistic (-3.591) is lower than the lower 5% point of the t-distribution at 9 degrees of freedom (-1.833).

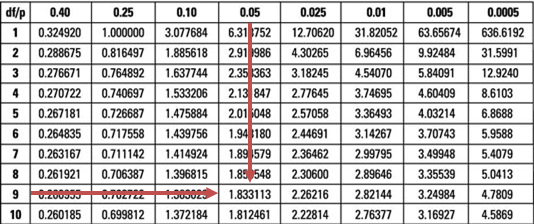
This gives us sufficient evidence to reject the H₀ at 5% significance. Therefore, it would be very reasonable to conclude that the special diet reduces body weight.

Question

Repeat the example above using a significance level of just 0.05% and state the decision rule.

A. Reject the H₀ and conclude that the special diet reduces body weight.

B. Do not reject the H₀ and conclude that the special diet has an insignificant effect on body weight.

C. Reject the H₀ and conclude that the special diet has an insignificant effect on body weight.

Solution

The correct answer is B.

The observed test statistic still remains -3.591. The lower 0.05% point of the t₉ distribution is -4.781.

It is clear that the test statistic is way above the t₉ distribution, i.e., it lies outside the critical or rejection region. Therefore, we would not reject the H₀.

Note to candidates: Reducing the significance level basically reduces the probability of rejecting a true null hypothesis (type I error).