Key Rate Duration

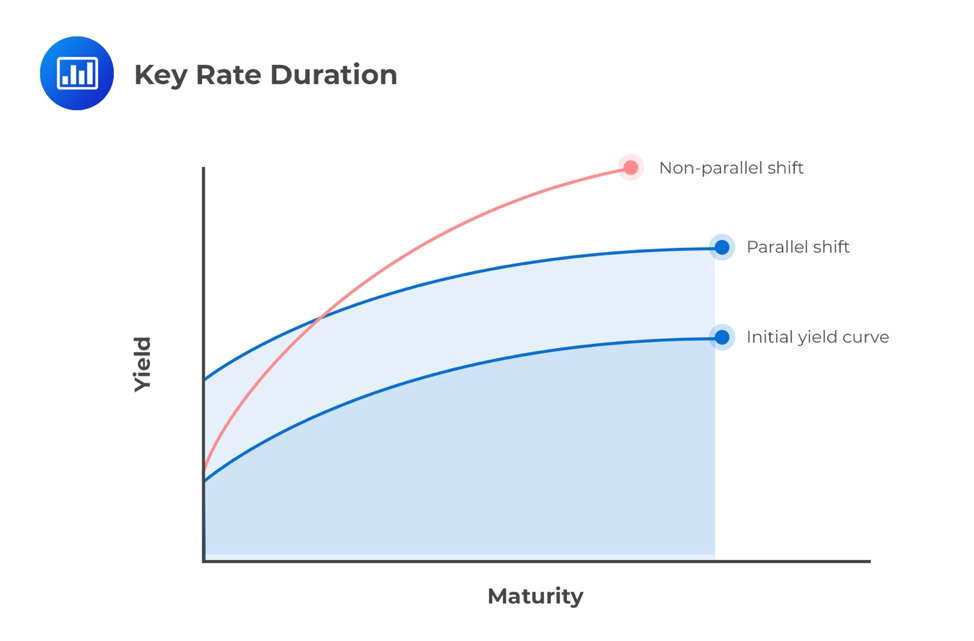
The effective duration calculates expected changes in price for a bond or portfolio of bonds given a basis point change in yield. This, however, is only valid for parallel shifts in the yield curve. The key rate duration presents an improvement to the effective duration because it gives the expected changes in price when the yield curve shifts in a manner that is not perfectly parallel. In other words, it measures a security’s sensitivity to shifts at “key” points along the yield curve.

The key rate formula is similar to the effective duration formula, except that it uses 0.01 in the denominator to reflect a 1% (100 basis points) change in the yield at a specific point on the yield curve:

$$ \text{Key rate duration} =\frac { { PV }_{ – }-{ { PV }_{ + } } }{ 2\times 0.01 \times { PV }_{ 0 } } $$

Where:

\({ PV }_{ – }\) = the bond price after a 1% decrease in yield

\({ PV }_{ + }\) = the bond price after a 1% increase in yield

\({ PV }_{ 0 }\) = the original bond price

Example: Key Rate Duration

A bond is originally priced at $1,000. With a 1% increase in yield for a certain maturity on the yield curve, the bond’s price would decrease to $980. A 1% decrease in the same yield, would occasion a rise of the price to $1,030. Based on the formula above, the key rate duration of the bond would be:

$$ KRD =\frac { { 1,030 }-{ 980 }}{ 2\times 0.01 \times { 1,000 } } =2.5$$

Why Use Key Rate Duration?

A financial analyst may want to know how the price of the callable bond is expected to change if benchmark rates at short maturities shift by a specific number of basis points, but longer maturity benchmark rates remain constant. This case would represent a flattening of the yield curve, given that the yield curve is upward sloping. For parallel shifts in the benchmark yield curve, key rate durations could indicate the same interest rate sensitivity as effective duration. 

Interpretation of Key Rate Duration

Interpreting each key rate duration in isolation can be quite difficult. That is because, in practice, it’s highly unlikely that a single point on the yield curve will exhibit an upwards or downwards shift while all other points remain constant. For this reason, analysts tend to compare key rate durations across the curve.

Question

The key rate duration formula is similar to which of the following formulas?

1. Effective duration.
2. Modified duration.
3. Macaulay duration.

Solution

The correct answer is A.

The key rate formula is similar to the effective duration formula, except that it uses 0.01 in the denominator to reflect a 1% change in the yield at a specific point on the yield curve: