Types and Measures of Unemployment
[vsw id=”IP3HiHY1YA0″ source=”youtube” width=”611″ height=”344″ autoplay=”no”] Unemployment happens when individuals who are capable... Read More
A supply function is a mathematical expression that represents the relationship between the units of quantity of a product or service demanded, its price, and other deterministic factors such as input costs, prices of substitutes, etc. The dependent variable is the quantity supplied, while the associated factors are independent.
In a free market, the cost curves find the optimal production point. This is the point where costs are minimized, and profits maximized. Individual firms’ supply curves are positively sloped. Thus, an increase in price causes an increase in supply. In this case, the supplied quantity is dependent on the market prices, while the price is dependent on the quantity available in the market.
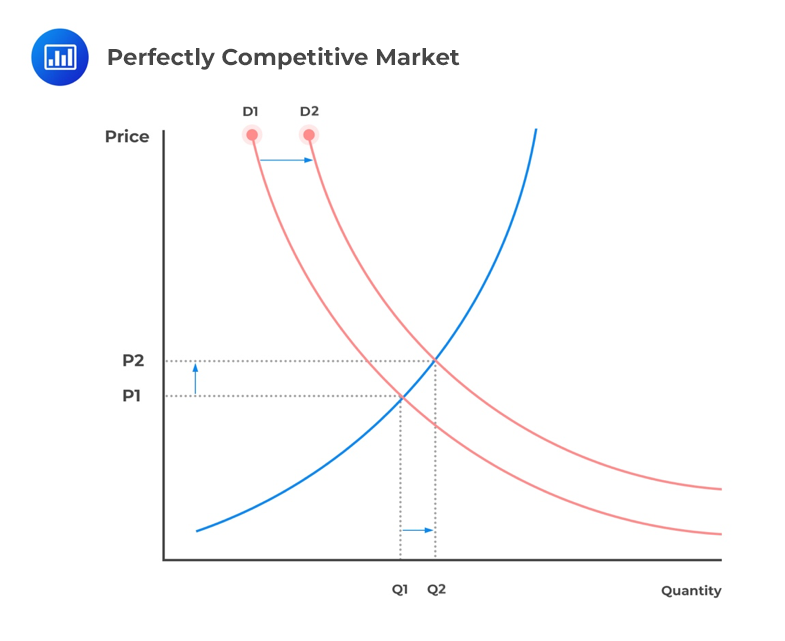
As demand rises from D1 to D2, the quantity supplied rises from Q1 to Q2, and the price also rises from P1 to P2.
Assume that the supply function of a product is given by:
\(Q_s=20+10P\)
Where \(Q_s\)= quantity supplied, and \(P\)=Price
Calculate the quantity supplied if the price of the product is currently $10.
Using the function \(Q_s=20+10P\), substitute \(P=10\) so that the quantity supplied is:
\(Q_s=20+10\times 10=120 \) units
The supply function of a monopoly is purely based on the cost structure of the firm. However, it is important to note that a monopoly does not have a purely defined supply function.
Thus, the optimal output level and price are not determined by any supply curve. Here, the optimal output is based on the output levels that maximize profits. In a monopoly market, profit is maximized when marginal revenue equals marginal cost, i.e., MR=MC.
The supply function of oligopolies is also not well-defined. Therefore, the optimal points of an oligopoly cannot be determined without including demand conditions. The strategies of competitors need to be considered.
However, the cost function is useful in determining the optimal supply level. In this case, it still holds that at the optimal points, MR = MC. If a dominant firm exists, it becomes the price maker while the remaining firms are all price takers.
Let:
\(M\) = price maker
\(T\) = price taker
The price maker first identifies its profit-maximizing output \(MR_M = MC_M\) with an output \(Q_M\). Its price will depend on its portion of the total demand \(D_M\). When the price is \(P_M\), the price maker will supply \(Q_M\) of the total demand \(Q_T\). The price takers will, therefore, supply \(Q_T-Q_M = Q_F\).
From the above example, we can conclude that no single function can determine the quantity supplied.
In this market structure, the supply function is also not well-defined. The appropriate output level is determined by the point where the Marginal Cost and Marginal Revenue curves intersect (MC=MR).
However, it is important to note that the price will be charged in accordance with the demand schedule of the market. The supply curve of a firm should measure the quantity that the firm is willing and able to supply at different price levels. Unfortunately, the marginal revenue and marginal cost do not include this information.
Question
Which forms of market structures have a purely defined supply function?
A. Perfect competition
B. Perfect competition and monopolistic competition
C. Perfect competition, monopolistic competition, and oligopoly
Solution
The correct answer is A.
Only perfect competition has a defined supply function.
Option B is incorrect. The supply curve of a firm under monopolistic competition should be able to measure the quantity that the firm is willing and able to supply at different price levels. Unfortunately, the marginal revenue and marginal cost do not include this information.
Option C is incorrect. The supply function of oligopolies is also not well-defined. Therefore, the optimal points of an oligopoly cannot be determined without including demand conditions. The strategies of competitors need to be considered.
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.