Financial Instruments
According to the IFRS, a financial instrument is a contract that gives rise... Read More
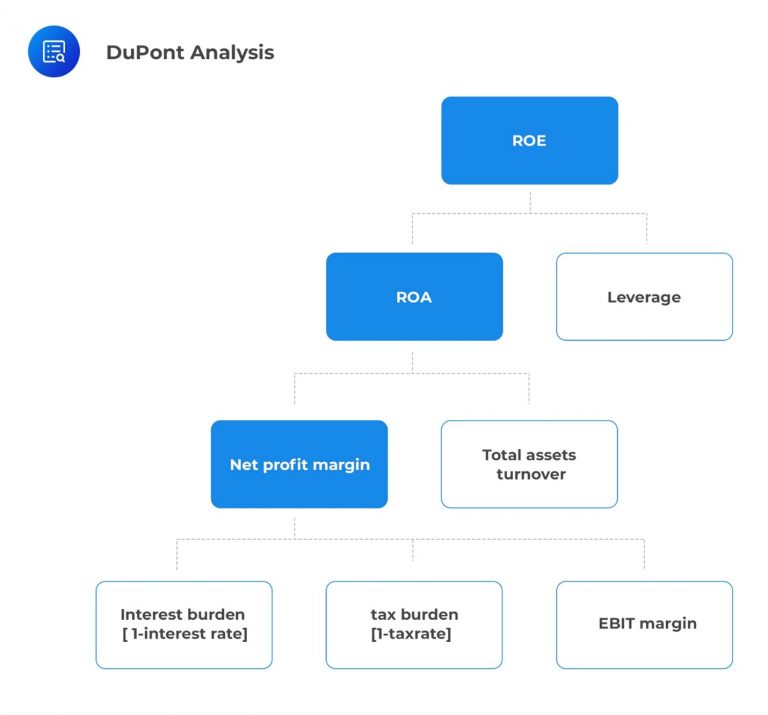
Recall that, return on equity (ROE) measures the return a company generates on its equity capital. To understand the factors driving a company’s ROE, it is helpful to decompose ROE into its component parts, a technique often referred to as DuPont analysis, originally developed by DuPont.
DuPont anlysis involves expressing the basic ratio of net income divided by average shareholders’ equity as the product of several component ratios. Each of these component ratios reflects a distinct aspect of the company’s performance that influences ROE.
So what is the significance of DuPont analysis? Decomposing ROE helps evaluate how different aspects of performance, such as efficiency, operating profitability, taxes, and financial leverage, impact the company’s profitability. Moreover, DuPont analysis is valuable for understanding changes in ROE over time for a particular company and for comparing ROE between different companies during a specific period.
Lastly, management can use the analysis to identify areas for improvement to enhance ROE since DuPont analysis highlights the interconnectedness of various financial ratios and their collective influence on the return generated for the company’s equity investors.
Analysts have devised various methods for decomposing ROE (Return on Equity). One of the most commonly used methods involves decompositing ROE into two components. Recall that:
$$ ROE=\frac {\text{Net income}}{\text{Average shareholders’ equity}} $$
We can decompose ROE as follows:
$$ \begin{align}\text{ROE}&=\frac {\text{Net income}}{\text{Average shareholders’ equity}}\\&=\left(\frac {\text{Net income}}{\text{Average total assets}} \right) \times \left(\frac {\text{Average total assets}}{\text{Average shareholders’ equity}}\right) \\ \Rightarrow \textbf{ROE}&=\textbf{Return on Assets (ROA)}\times \textbf{Leverage}\end{align} $$
This implies that ROE is determined by a company’s ROA and its financial leverage.As such, a company can boost its ROE by either enhancing its ROA or by increasing its leverage.
Recall that leverage is calculated as average total assets divided by average shareholders’ equity. If a company had no leverage (no liabilities), its leverage ratio would be 1.0, making ROE equal to ROA. As a company assumes more liabilities, its leverage increases.
As long as a company can borrow at a rate lower than the return it earns on the borrowed funds, it is effectively using leverage, which increases ROE. Conversely, if the borrowing cost exceeds the return on investment, increased leverage will decrease ROE because borrowing would reduce ROA.
Just as ROE can be decomposed, its individual components, like ROA, can also be broken down. By further decomposing ROA, we can express ROE as a product of three component ratios:
$$\begin{align}
\text{ROE} &= \frac {\text{Net income}}{\text{Average shareholders’ equity}}\\
&= \left( \frac {\text{Net income}}{\text{Revenue}} \right) \times \left( \frac {\text{Revenue}}{\text{Average total assets}} \right) \\
&\times \left( \frac {\text{Average total assets}}{\text{Average shareholders’ equity}} \right) \\
\Rightarrow \textbf{ROE} &= \textbf{Net profit margin} \times \textbf{Total asset turnover} \times \textbf{Leverage}
\end{align}$$
This decomposition illustrates that a company’s ROE is influenced by its net profit margin, efficiency, and leverage.
The net profit margin indicates profitability by showing how much income a company earns per monetary unit (e.g., euro or US dollar) of sales. The asset turnover ratio reflects efficiency by measuring how much revenue a company generates per monetary unit of assets.
Essentially, ROA is decomposed into net profit margin and total asset turnover. A company’s ROA is thus a function of its profitability (net profit margin) and efficiency (total asset turnover).
The third term on the right-hand side of the equation is the equity multiplier, which measures financial leverage by indicating the total amount of a company’s assets relative to its equity capital.
To further separate the effects of taxes and interest, the net profit margin can further be decomposed, leading to:
$$ \begin{align}\text{ROE}&=\frac {\text{Net income}}{\text{Average shareholders’ equity}}\\ &=\left( \frac {\text{Net income}}{EBT} \right)\times \left(\frac {EBT}{\text{EBIT}} \right) \times \left( \frac {\text{EBIT}}{\text{Revenue}} \right) \\ & \times \left( \frac {\text{Revenue}}{\text{Average total assets}} \right) \\ & \times \left(\frac {\text{Average total assets}}{\text{Average shareholders’ equity}} \right) \\ \Rightarrow \textbf{ROE} & =\textbf{Tax burden} \times \textbf{Interest Burden} \times \textbf{EBIT margin} \\ & \times \textbf{Total asset turnover} \times \textbf{Leverage} \end{align} $$
This 5-way decomposition is the Dupont Analysis method found in financial databases such as Bloomberg.
The tax burden measures the impact of taxes on ROE, representing one minus the average tax rate, or the portion of a company’s pretax profits that it retains. In other words, tax burden can be expressed in decimal or percentage form. For example, a 35 percent tax rate would yield a factor of 0.65 or 65%. Consequently, a higher value for the tax burden indicates that the company retains a larger portion of its pretax profits, reflecting a lower tax rate. Conversely, a decrease in the tax burden ratio indicates a higher tax rate, leaving the company with a smaller portion of its pretax profits.
The interest burden reflects the impact of interest on ROE, with higher borrowing costs leading to a reduction in ROE. Some analysts prefer using operating income instead of EBIT for this term and the following one. Either operating income or EBIT is acceptable if used consistently. In such cases, the second term would measure both the impact of interest expense and non-operating income on ROE.
EBIT margin measures the effect of operating margin if operating income is used or EBIT margin if EBIT is used on ROE. This term primarily assesses the impact of operating profitability on ROE.
The total asset turnover ratio indicates the overall efficiency of the company in generating revenue per unit of total assets.
The financial leverage ratio measures the total amount of a company’s assets relative to its equity capital.
The figure below illustrates the idea behind DuPont’s analysis.
Question 1
A company has the following financial data:
$$
\begin{array}{l|r}
\text{Net profit margin} & 17.54\% \\ \hline
\text{Revenue} & 285,000 \\ \hline
\text{Average total assets} & 1,000,000 \\ \hline
\text{Average shareholders’ equity} & 600,000 \\ \hline
\end{array}
$$Using the three-step DuPont method, the company’s ROE is <em>closest to</em>:
- 5.29%
- 8.33%
- 1.14%
Solution
The correct answer is B.
$$ ROE = \left( \frac{\text{Net income}}{\text{Revenue}} \right) \times \left( \frac{\text{Revenue}}{\text{Average total assets}} \right) \times \left( \frac{\text{Average total assets}}{\text{Average shareholders’ equity}} \right)$$
Where:
$$\begin{align}\text{Net Profit Margin}&=\frac{\text{Net income}}{\text{Revenue}} = 17.54\% = 0.1754\\\text{Total Asset Turnover}&=\frac{\text{Revenue}}{\text{Average total assets}}= \frac{285,000}{1,000,000} = 0.285\\\text{Leverage (Equity Multiplier)}&=\frac{\text{Average total assets}}{\text{Average shareholders’ equity}}= \frac{1,000,000}{600,000} = 1.667\end{align}$$
As such,
$$\text{ROE} = 0.1754 \times 0.285 \times 1.667 = 8.33\%$$
Get Ahead on Your Study Prep This Cyber Monday! Save 35% on all CFA® and FRM® Unlimited Packages. Use code CYBERMONDAY at checkout. Offer ends Dec 1st.