GMAT® Data Sufficiency Questions
Get Access to 1,000 Exam-Style Questions
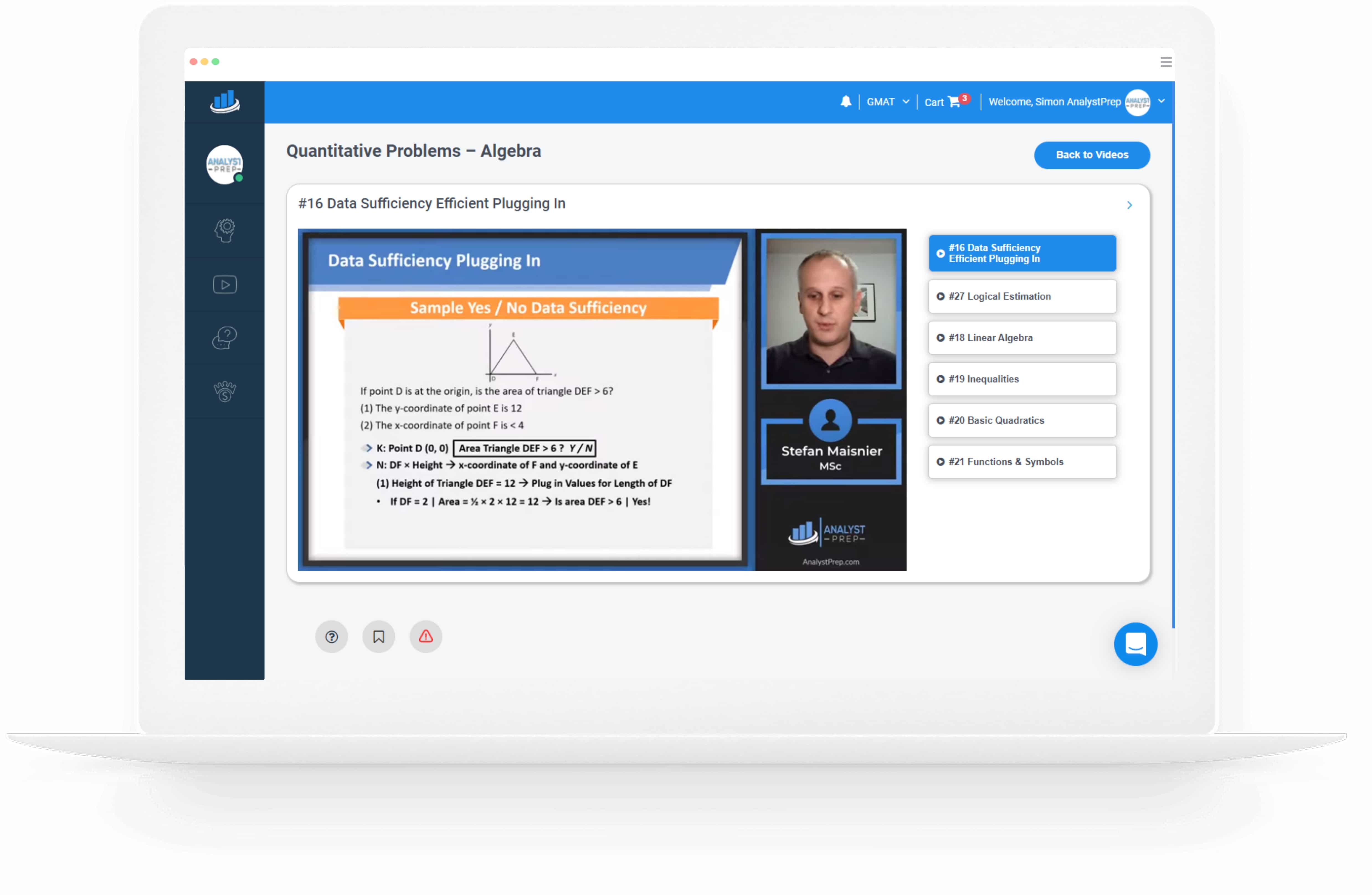
What is the Structure of GMAT Data Sufficiency Questions?
Data Sufficiency questions is one of the sections in Quantitative reasoning questions (the other one is Problem-solving questions). Data Sufficiency questions are designed to measure your ability to analyze a quantitative problem, ascertain which data is relevant, and decide the extent to which there is enough data to solve the problem.
A data sufficiency question consists of a question and two statements. To answer the question, one should first identify the statement that provides information relevant to the question and then eliminate all the other possible answers by using math knowledge and other everyday facts. There will be 14 to 15 questions on data sufficiency in each quantitative section.
Tips for Data Sufficiency Questions?
- The quantitative takes 62 minutes to complete and includes 31 questions. Therefore, you do have on average 2 minutes to answer each question.
- There are 14 to 15 data sufficiency questions in every quantitative section.
- Determine whether the problem allows only a single value or a range of values. Note that the primary objective is to determine whether there is enough data to solve the problem.
- Avoid unnecessary assumptions about geometrical figures, as they are not necessarily drawn to scale.
Questions Answered by our Users
Satisfied Customers
Preparation Platform By Review Websites
Some Free Exam-style GMAT Practice Questions offered by AnalystPrep
GMAT Quantitative Problems
Question 1
Division & Factoring
When integer y is divided by 2, is the remainder 1?
(1) \((-1)^{(y + 2)} = -1\)
(2) \(y\) is prime.
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
The correct answer is: A)
(1) That \((–1)^{(y + 2)} = -1\), dictates that y + 2 must be odd and therefore y is odd since only an odd exponent can produce a value < 0. Furthermore, if an odd number is divided by 2, the remainder must be 1; SUFFICIENT.
(2) That y is prime does not definitively identify y as definitively even or odd, so the remainder could be either 0 or 1; NOT SUFFICIENT.
The correct answer is A; statement 1 alone is sufficient.
Question 2
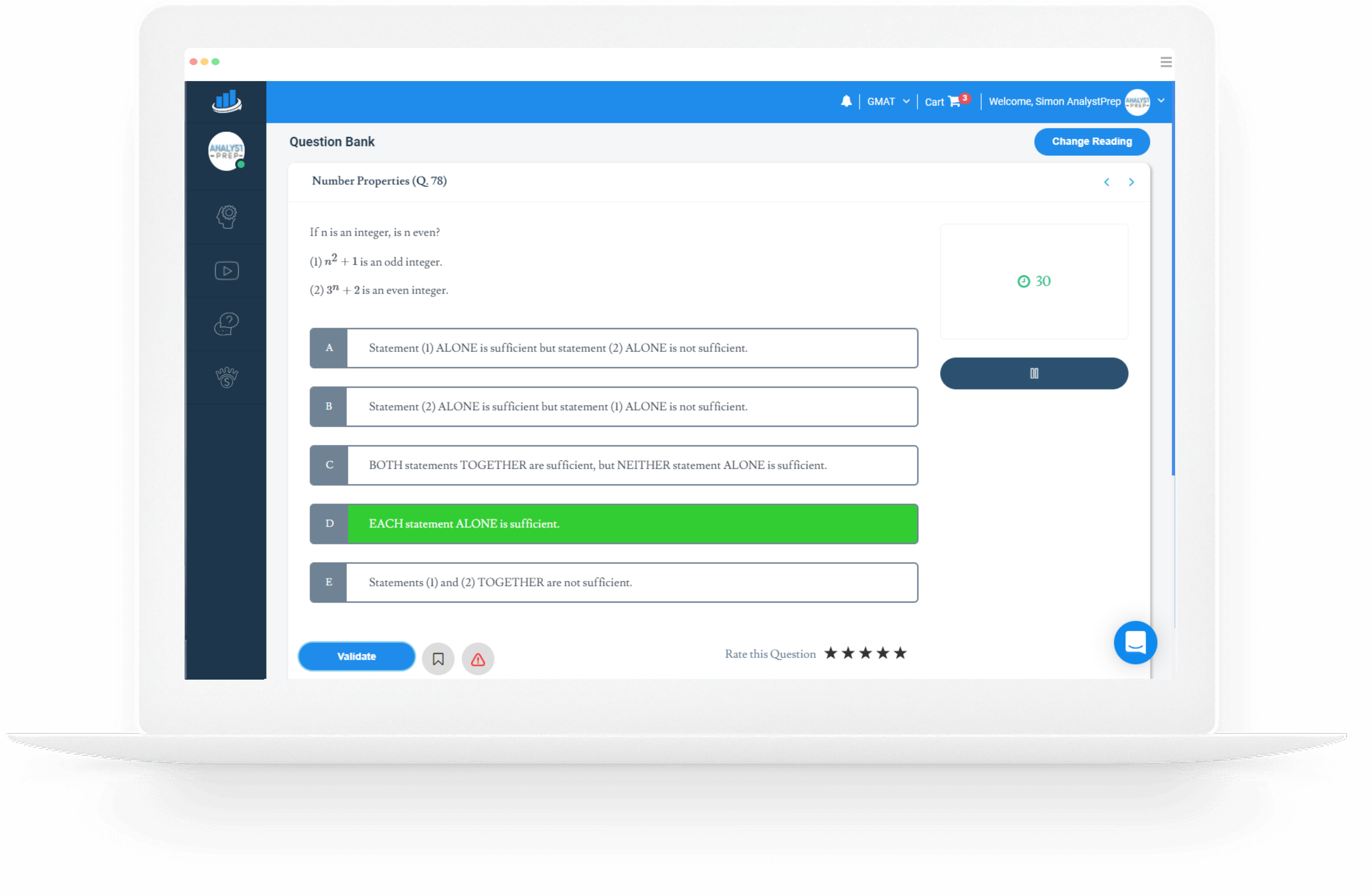
Number Properties
Chiku received a $3.50 per hour raise this week. If last week she worked 40 hours per week at her old pay rate, how many fewer hours can she work this week and still guarantee that she makes more this week than she did last week?
(1) She made $620 last week.
(2) Her raise was 20 percent greater than that of any of her coworkers.
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
The correct answer is: A).
(1) If Chiku made $620 last week, it is possible to solve for her old pay rate, then her new pay rate, and then the number of hours she’d need to work to guarantee she makes more this week than she did last week; SUFFICIENT.
(2) That her raise was greater than that of any of her coworkers introduces a new unknown variable; NOT sufficient.
The correct answer is A; statement 1 alone is sufficient.
Question 3
Percentages (Data Sufficiency)
If 60 percent of the freshman class at Westown High is male, does the freshman class have more than 100 male students?
(1) The freshman class has more than 150 students.
(2) The freshman class has 63 more male students than female students.
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
(1) Defining the total number of students in the freshman class as greater
than 150 does not determine the number of male nor female students
definitively, and so the question cannot be answered; NOT sufficient.
(2) Given:
- 60 percent of the freshman class is male.
- The freshman class has 63 more male students than female students.
Let’s use s to denote the total number of students in the
freshman class, m to represent the number of male students, and
f to represent the number of female students.
From the information given in statement (2):
$$\begin{align*}m&=f+63\\m&=0.60s\\f&=0.40s\end{align*}$$
We can set up the following equation using m and f:
$$0.60s=0.40s+63$$
Solving for s:
$$\begin{align*}0.20s&=63\\s&=\frac{63}{0.20}\\s&=315\end{align*}$$
Now, calculating the number of male students (m):
$$\begin{align*}m&=0.60s\\m&=0.60\times315\\m&=189\end{align*}$$
Therefore, the number of male students is 189, which is indeed more than
100.
Thus, statement (2) alone is sufficient to determine that there are more than
100 male students.
The correct answer is B: Statement (2) ALONE is sufficient but
statement (1) ALONE is not sufficient.
Question 4
Exponents & Radicals (Data Sufficiency)
The amount of bacteria in a culture after some \(t\) hours is given by the function \(f(t)=pe^{kt}\) where \(p\) is a constant. What is the number of bacteria after 8 hours?
(1) There were approximately 275 bacteria after 2 hours
(2) \(k=0.16\)
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
The correct answer is: C)
(1) From the function, \(f(t)=pe^{kt}\), when \(t=2, f(t)=275\). The equation becomes \(pe^{2k}=275\). This is one equation in two unknowns, hence, we cannot solve it. More information is required; NOT SUFFICIENT.
(2) When \(k=0.16\), we have \(f(t)=pe^{0.16t}\). In this case, \(p\) is unknown, hence more information is required; NOT SUFFICIENT.
Considering the two cases, we have \(pe^{2k}=275\) and \(f(t)=pe^{0.16t}\) which reduced to \(pe^{2(0.16)}=275\). We solve the equation
$$\begin{align*} pe^{2(0.16)} &=275\\
pe^{3.2} &=275\\
\ln \left(pe^{3.2}\right) &=\ln 275\\
\ln p + 3.2 &=\ln 275\\
\ln p &=\ln 275 – 3.2 = 2.41677\\
p& =e^{2.41677}=11.21\end{align*}$$.
We now solve the equation
When \(t=8\), we have
$$f(8)=11.21e^{0.16(8)} =11.21e^{1.28}=40.32$$
The correct answer is C; BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
Question 5
3D Geometry (Data Sufficiency)
A cylindrical layer cake has two vanilla layers surrounding a marzipan layer, represented by the shaded region, as shown below. Is the cake split into three layers of equal volume?
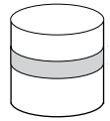
(1) The height of marzipan layer is equal to the radius of the whole cake.
(2) The volume of the entire cake is 81π cubic inches.
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
The correct answer is: E)
Note that the volume for a cylinder can be found from the formula \(πr^2 × height\) where r = radius and the height is perpendicular to the radius.
(1) That the height for the marzipan layer is equal to the radius of the cake means that the volume of the marzipan layer can be found from the simplified formula \(πr^3\), but the total cake volume remains dependent on the actual height of the cake; NOT sufficient.
(2) Represent the information algebraically as \(πr^2 × height = 81\), but no information is provided about the height in relation to the radius; NOT sufficient.
(Together) The information together still does not relate the height to the radius.
For instance the radius could be 3 and the ratio of the marzipan layer to the others could be equal as each would have a volume of 27π.
Alternatively, the radius could = 1 and the marzipan layer would be significantly smaller than the other two layers.
The correct answer is E; both statements together are still not sufficient.
Question 6
Inequalities
At Rounders Grocer, orange slices cost $2 a pound, pineapple chunks cost $3 a pound, and cut watermelon cost $5 a pound. If Sally buys enough of these three fruits from Rounders to make five pounds of fruit salad, and at least one pound of each, which fruit did she buy the most of by weight?
(1) Sally spent less than $5 on orange slices.
(2) Sally spent more than $18 on her fruit salad.
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
The correct answer is: B)
First note that Sally must buy at least one pound of each of the fruits, which would result in a sum fixed cost of $10.
(1) If Sally spent less than $5 on orange slices, then she spent must have spent more on one of the other two fruits, but it is unclear which; NOT sufficient
(2) If Sally spent more than $18 then she must spend more than $8 on the two-variable pounds of fruit, which could only be accomplished by buying two more pounds of cut watermelon; Sufficient
The correct answer is B; statement 2 alone is sufficient.
Question 7
Plane Geometry
The Embeyay Expressway and Emefay Expressway intersect at a perpendicular junction coming from Ulster City and Finster Town, respectively, while a direct road connecting the two municipalities is entirely straight. How much further would a motorist traveling the expressways between Ulster City to Finster Town have to drive in comparison to another motorist who used the direct road?
(1) The distance from Ulster City to the Embeyay Expressway and Emefay Expressway junction is 12 kilometers.
(2) The distance from Ulster City to Finster Town on the direct road is 15 kilometers.
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
The correct answer is: C)
Recognize that a right triangle can be formed with the junction creating the 90° angle and the two municipalities at the other two vertices.
Therefore, only two of the distances between the locations will be necessary to find the third by way of the Pythagorean Theorem.
(1) This provides the distance for one of the two legs of the right triangle only; NOT sufficient.
(2) This provides the distance for the hypotenuse of the right triangle only; NOT sufficient.
(Together) Complete the theorem as \(12^2+b^2 =15^2\) to find that the shorter leg distance is 9. From there, 12 + 9 = 21 is 6 kilometers further than 15 kilometers; SUFFICIENT.
Question 8
Descriptive Statistics
A supermarket display of canned corn is shaped like a pyramid with one can on top and two more cans in each row below. If the display is only one can deep for the entire pyramid, what is the median number of cans in a row in the pyramid?
(1) There are 100 cans in the pyramid.
(2) The range of cans per row is 18.
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
The correct answer is: D).
Remember that if there is a constant difference in terms that the average for the sequence = median of the sequence.
The formula for average is sum divided by the number of terms, so in this case the total number of cans = median × number of rows.
And the total number of cans = x + (x + 2) + (x + 4) … up to the total number of rows.
Therefore, two equations are already theoretically known, and only one additional equation is needed to solve for all of the values involved.
(1) If 100 is the total number of cans, then it would be possible to count from 1 + 3 + 5 + 7… to determine the total number of rows, and thereby the median, without completing the process; SUFFICIENT.
(1)If the range in cans per row is 18, then it would be possible to determine that the number of cans in the last row is 19 and from there the median, without completing the process; SUFFICIENT
The correct answer is D; each statement alone is sufficient.
Question 9
Coordinate Geometry
If line \(d\) in the coordinate plane has the equation \(y = mx + b\), where \(m\) and \(b\) are constants, what is the slope of line \(d\)?
(1) Line \(d\) intersects the line with equation \(y = 6x + 2\) at the point (1, 8).
(2) Line \(d\) is parallel to the line with equation \(y = (2 – m)x + b – 4\).
A) Statement (1) ALONE is sufficient but statement (2) ALONE is not sufficient.
B) Statement (2) ALONE is sufficient but statement (1) ALONE is not sufficient.
C) BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
D) EACH statement ALONE is sufficient.
E) Statements (1) and (2) TOGETHER are not sufficient.
The correct answer is: B)
Note that the slope of a line with equation \(y = mx + b\) is\( m\).
(1) A line passing through the point (1, 8) can have any value for its slope, so it is impossible to determine the slope of line \(d\).
For example, the line \(y = x + 7\) intersects \(y = 6x + 2\) at (1, 8) with a slope of 1, while the line \(y = 2x + 6\) intersects \(y = 6x + 2\) at (1, 8) with a slope of 2; NOT sufficient.
(2) Parallel lines have the same slope, and it is possible to solve for the slope as \(m = 2 – m\), \(2m = 2\), and \(m = 1\); SUFFICIENT.
GMAT® Prep Packages
You can combine both tools with the Learn + Practice Package for $229.
GMAT Practice Package
$
139
/ 12-month access
- Quantitative Practice Problems
- Verbal Practice Problems
- Integrated Reasoning Practice Problems
- Customizable Quizzes
- Performance Tracking Tools
GMAT Learn + Practice Package
$
229
/ 12-month access
- Conceptual Video Lessons
- Quantitative Practice Problems
- Verbal Practice Problems
- Integrated Reasoning Practice Problems
- Customizable Quizzes
- Performance Tracking Tools
GMAT Learn Package
$
139
/ 12-month access
- Conceptual Video Lessons