Comprehensive CFA® Level 2 Study Notes to Ace Your Exam
Every Learning Outcome Statement (LOS) Summarized with Question Examples
Tackling the CFA® Level 2 curriculum can feel like trying to climb a mountain. With over 5,000 pages of material in the CFA Institute’s official books, covering 10 topic areas, it’s easy to feel overwhelmed by the sheer amount of information you need to memorize and understand. But don’t worry, we’ve got you covered.
We’ve simplified the journey by creating comprehensive study notes that break down every Learning Outcome Statement (LOS) into easy-to-read summaries, complete with practice questions that mimic real exam scenarios. Our notes help you grasp complex concepts faster and more efficiently, so you can focus on what really matters: mastering the material.
“Did you know that the CFA Institute recommends spending at least 300 hours preparing for each level? “
That’s about six months of dedicated study time just for Level 2! And with pass rates hovering around 40% over the last decade, it’s clear that you’ll need to go above and beyond the average candidate to succeed. In fact, a 2015 survey by the CFA Institute found that over 60% of candidates used third-party study materials in addition to the official curriculum. That’s why we designed our CFA Level 2 Study Materials to give you an edge, streamline your study process, and help you feel confident going into exam day.
Questions Answered by our Users
Satisfied Customers
Cfa Preparation Platform By Review Websites
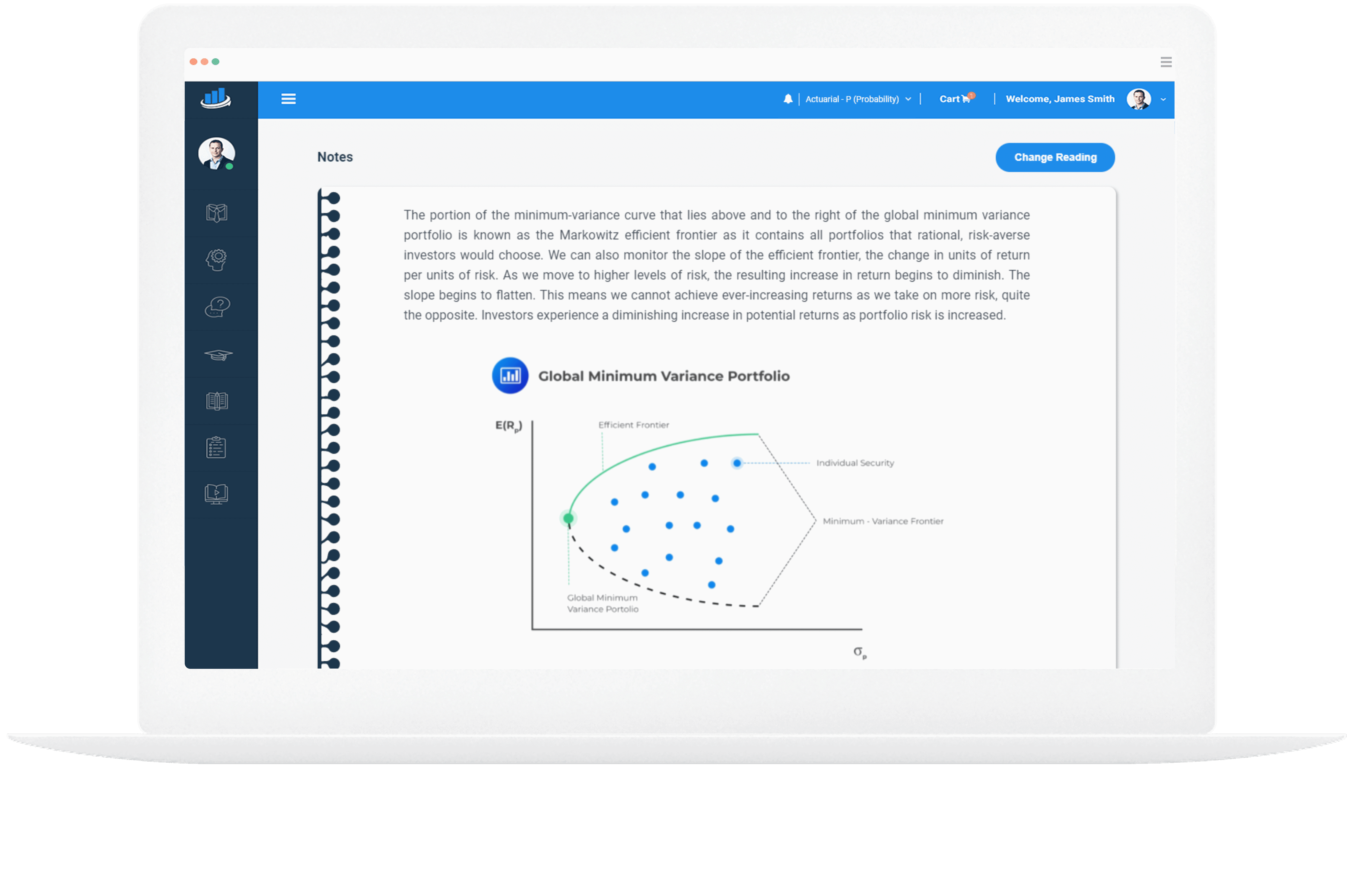
Why Over 2000 Candidates Love AnalystPrep's CFA® Level 2
Study Notes
Our CFA Level 2 Study Notes, designed by CFA charterholders, have one goal: making your study process as efficient and stress-free as possible.
We know how overwhelming the CFA Level 2 curriculum can be, so we’ve summarized each chapter into clear, digestible pieces that focus on the most important concepts you need to know to ace the exam.
Here’s what’s included:
- Chapter Summaries: Each chapter is broken down into clear, digestible pieces, making it easier to understand and absorb the most important concepts.
- End-of-LOS Practice Questions: You’ll find questions after each Learning Outcome Statement to test your understanding and mimic real exam scenarios.
- Tips and Tricks: Gain expert insights and strategies for tackling challenging topics like Financial Reporting and Portfolio Management, helping you navigate the most complex parts of the curriculum.
Whether you’re working through quantitative methods or trying to master derivatives, our study notes make it easy to stay on track.
And whenever you hit a roadblock, our team of expert instructors is here to help.
CFA® Level II Study Packages by AnalystPrep
Add video lessons and study notes for only $150 extra.
Combine all three levels, with lifetime access and unlimited ask-a-tutor questions for only $799.
Practice Package
$
349
/ 12-month access
- Question Bank
- CBT Mock Exams
- Performance Tracking Tools
Learn + Practice Package
$
499
/ 12-month access
- Question Bank
- CBT Mock Exams
- Performance Tracking Tools
- Video Lessons
- Study Notes
Unlimited Package (All 3 Levels)
$
799
/ lifetime access
- Question Banks for all three Levels of the CFA Exam
- Mock Exams for all three Levels of the CFA Exam
- Performance Tracking Tools
- Video Lessons for all three Levels of the CFA Exam
- Study Notes for all three Levels of the CFA Exam
This isn't a Sprint, It's a Marathon
Stay on Course with our Study Plans
Staying organized is key to success. That’s why we offer customized study plans to fit your schedule, whether you prefer a one-month sprint or a two-month steady pace. We’ll guide you through the most important chapters and show you how to prioritize based on the CFA Level 2 topic weights, because not all topics carry the same importance in the exam.
Here’s a breakdown of the CFA Level 2 topics and their weightings to help you focus on the areas that matter most:
| Topic | Weight (%) |
| Ethical and Professional Standards | 10 – 15% |
| Quantitative Methods | 5 – 10% |
| Economics | 5 – 10% |
| Financial Reporting and Analysis | 10 – 15% |
| Corporate Issuers | 5 – 10% |
| Equity Investments | 10 – 15% |
| Fixed Income | 10 – 15% |
| Derivatives | 5 – 10% |
| Alternative Investments | 5 – 10% |
| Portfolio Management | 10 – 15% |
By knowing how much each topic is weighted, you can better prioritize your study time and make sure you’re prepared for the most heavily weighted sections.
Get Support Whenever You Need It
With AnalystPrep, you’re never studying alone. Our premium members have access to a supportive community and expert help whenever they need it. Got a question about the CFA Level 2 curriculum or need help with a tricky topic? Our team of experts will get back to you within 24 hours. Plus, our in-app forum connects you with other candidates, CFA charterholders, and even the founders of AnalystPrep, keeping you motivated and on track throughout your journey.
Example LOS from our Study Notes
Might you also be looking to test your knowledge with mock exams or practice questions?
Our CFA Level 2 mock exams are designed to simulate the actual exam format, with vignette-supported multiple-choice questions. They’ll help you get familiar with the structure, practice under timed conditions, and pinpoint areas needing improvement. Each mock exam comes with detailed explanations, so you can learn from your mistakes and prepare confidently.
If you’re looking to sharpen specific areas of your understanding, our CFA Level 2 practice questions offer targeted testing on each topic.
Try Our Practice Questions Here
Testimonials
“Thanks to your program I passed the first level of the CFA exam, as I got my results today. You guys are the best. I actually finished the exam with 45 minutes left in [the morning session] and 15 minutes left in [the afternoon session]… I couldn’t even finish with more than 10 minutes left in the AnalystPrep mock exams so your exams had the requisite difficulty level for the actual CFA exam.”
James B.
“I loved the up-to-date study materials and Question bank. If you wish to increase your chances of CFA exam success on your first attempt, I strongly recommend AnalystPrep.”
Jose Gary
“Before I came across this website, I thought I could not manage to take the CFA exam alongside my busy schedule at work. But with the up-to-date study material, there is little to worry about. The Premium package is cheaper and the questions are well answered and explained. The question bank has a wide range of examinable questions extracted from across the whole syllabus. Thank you so much for helping me pass my first CFA exam.”
Brian Masibo
“Good Day!
I cleared FRM Part I (May-2018) with 1.1.1.1. Thanks a lot to AnalystPrep and your support.
Regards,”
Aadhya Patel
“@AnalystPrep provided me with the necessary volume of questions to insure I went into test day having in-depth knowledge of every topic I would see on the exams.”
Justin T.
“Great study materials and exam-standard questions. In addition, their customer service is excellent. I couldn’t have found a better CFA exam study partner.”
Joshua Brown
“I bought their FRM Part 1 package and passed the exam. Their customer support answered all of my questions when I had problems with what was written in the curriculum. I’m planning to use them also for the FRM Part 2 exam and Level I of the CFA exam.”
Zubair Jatoi
“I bought the FRM exam premium subscription about 2 weeks ago. Very good learning tool. I contacted support a few times for technical questions and Michael was very helpful.”
Jordan Davis
FAQs
Is CFA Level 2 very hard?
Is 3 months enough for CFA Level 2?
Can I bring notes to the CFA exam?
What is the fail rate for CFA Level 2?
What are CFA Level 2 summary notes?
Where can I find CFA Level 2 study materials?
How many hours should I study for CFA Level 2?
What are the most important topics in CFA Level 2?
Are AnalystPrep CFA Level 2 notes reliable?
What is included in AnalystPrep’s CFA Level 2 notes?
