Exotic Options
After completing this reading, you should be able to: Define and contrast exotic... Read More
After completing this reading, you should be able to:
Options can be arranged in different ways to form different payoff patterns.
Strategies that involve a single option are referred to as spreads, while those involving both call and put options are referred to as combinations.
In the previous chapter, we looked at the put-call parity relationship, which is given by:
$$c + PV(K)= p + S_0………….(i)$$
Where:
\(c =\) Value of call option
\(K =\) Strike price
\(p =\) Value of put option
\(S_0=\) Initial stock price
\(r =\) Risk-free rate
\(T =\)Time to maturity
\(PV(K) =\) Present value of the strike price
The above result can also be expressed as:
\(S_0-c=PV(K)-p\)……………(ii)
\(-p -S_0=-c-PV(K)\)………(iii)
\(c -S_0=p-PV(K)\)…………(iv)
The right-hand side of equation (i) shows a combination of a put and an asset.
When you buy a put while holding the underlying asset, it is referred to as a protective put strategy.
The left-hand side of equation (ii) shows an asset plus a short call. This strategy is referred to as a covered call.
Equation iii shows the reverse of a protected put, while equation iv illustrates the reverse of a covered call.
A covered call describes a trading strategy where the seller (writer) of a call option also owns the underlying stock. The writer sells call options for the same amount (or less) of stock. If the option is not exercised, the writer gets to keep the premium. If the option is exercised, the writer simply hands the option buyer their shares. In a covered call, the important thing to note is that the investor receives a premium in exchange for giving up any potential profits from high upward movements of the asset price.
A covered call is the opposite of a naked call. In the latter, the writer of the call option does not own the underlying stock. However, in the event that the option is exercised, the writer is obligated to buy the shares at the market price and deliver them to the option buyer. A naked call, therefore, has an unlimited risk because the market price can rise unpredictably.
The holder of a covered call can only profit on the stock up to the strike price of the options contract. The maximum profit is capped at:
$$ \text{(Strike Price – Stock Entry Price) + Option Premium Received} $$
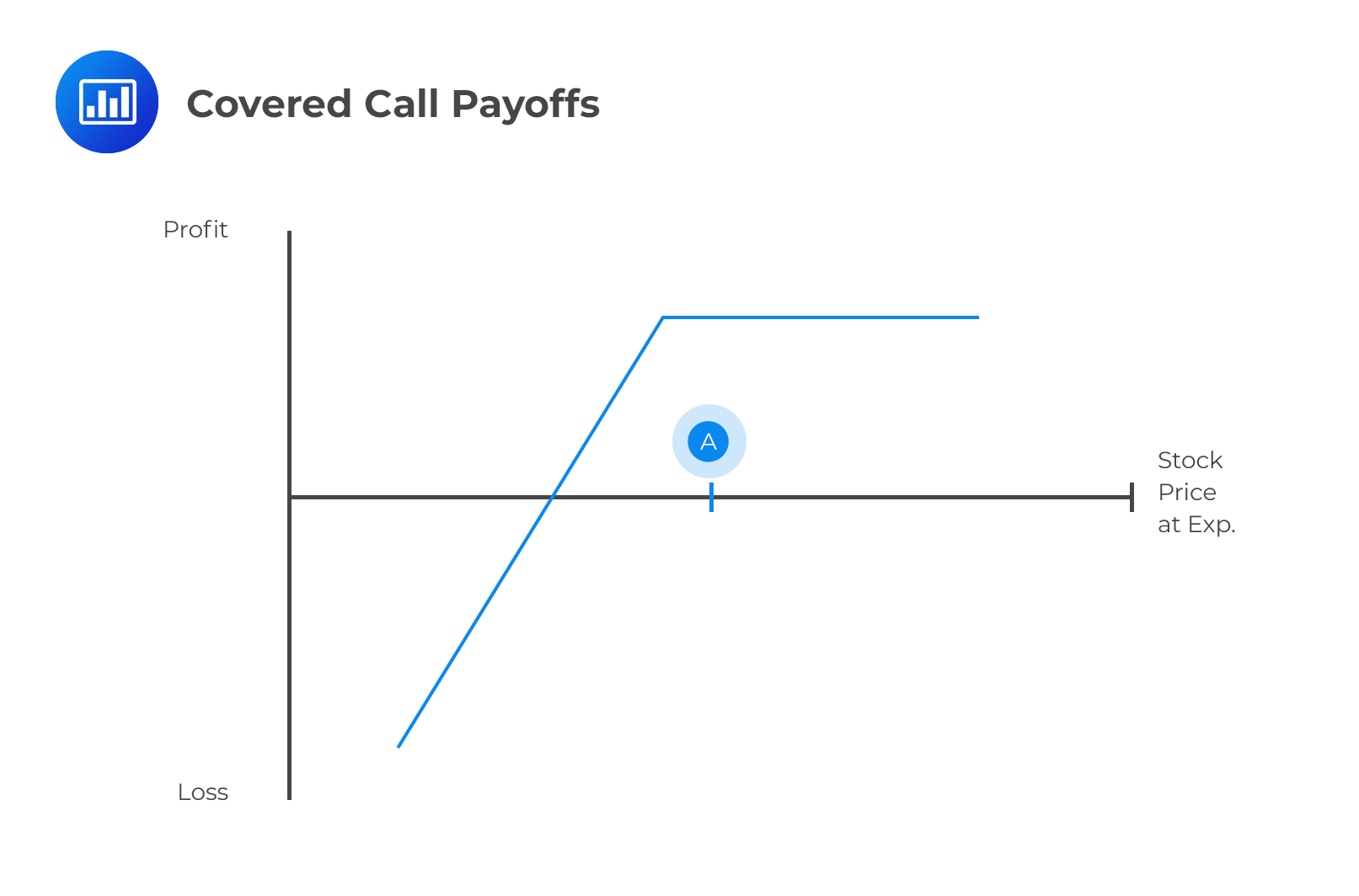 For example, let’s say you’ve bought a stock at $10, received a $0.50 option premium from selling a $12 strike price call. You’d maintain your stock position as long as the stock price stays below $12 at expiration. If the stock rises to \($13\), you will only profit up to $12, so your total profit will be \($2.5\left( =$12-$10+$0.50 \right) \). You’d be forced to give up the extra $0.50.
For example, let’s say you’ve bought a stock at $10, received a $0.50 option premium from selling a $12 strike price call. You’d maintain your stock position as long as the stock price stays below $12 at expiration. If the stock rises to \($13\), you will only profit up to $12, so your total profit will be \($2.5\left( =$12-$10+$0.50 \right) \). You’d be forced to give up the extra $0.50.
The maximum loss a covered call holder can incur is equal to:
$$ \text{Stock Entry Price}-$0+\text{Option Premium Received} $$
That could happen when the stock drops to $0.
For these reasons, a covered position is taken up to generate cash on a stock that is not expected to increase above the exercise price over the life of the option.
A protective put, also called a put hedge, is a hedging strategy where the holder of a security buys a put to protect themselves against a drop in the stock price of that security.
A protective put has unlimited profit potential. A profit is achieved when the underlying stock price exceeds its purchase price plus the premium paid for the option. On the other hand, the maximum loss is limited by the purchased put option and is equal to the premium paid for buying the put option.
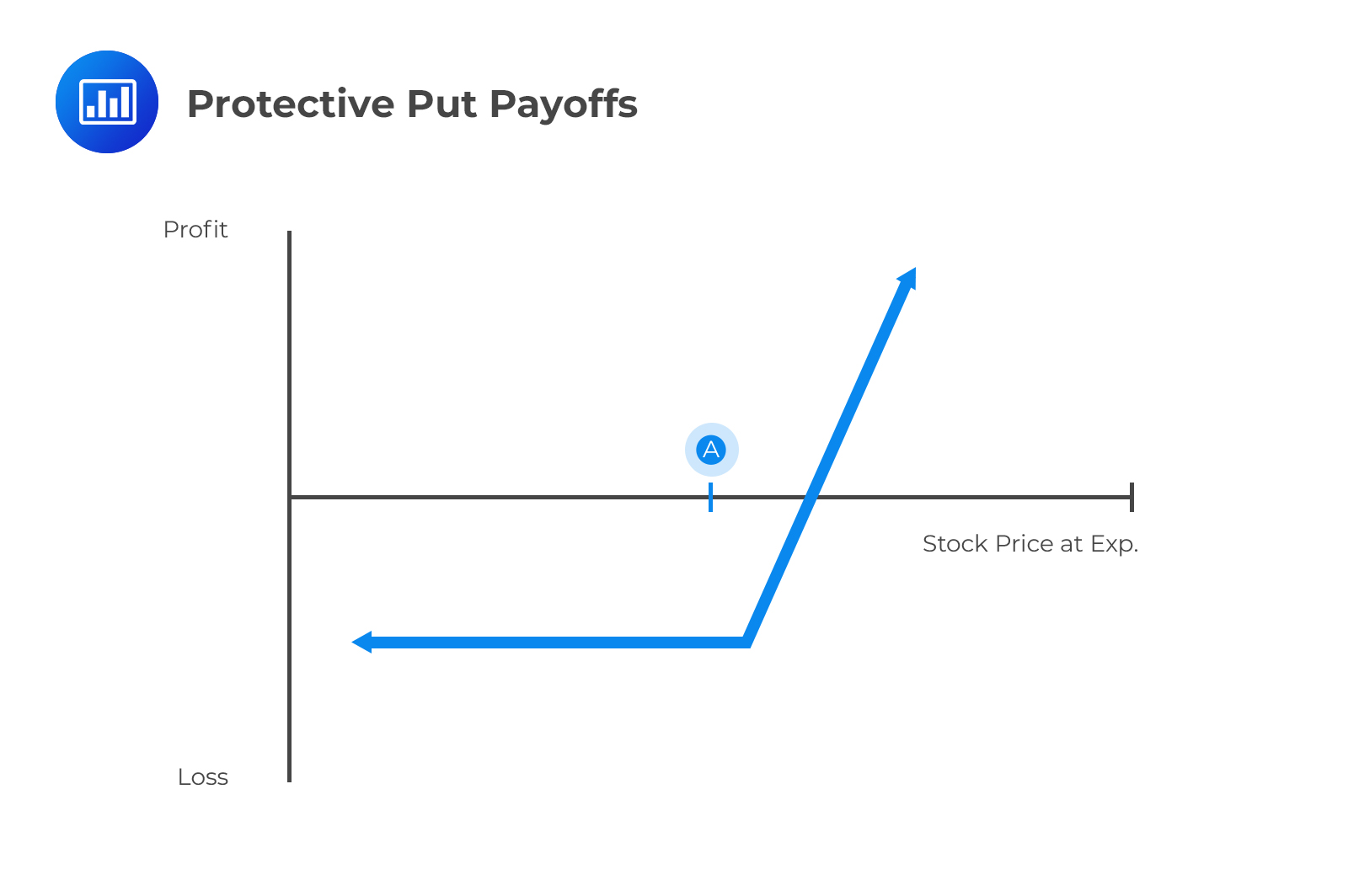 A protective put is taken by bullish investors worried about near-term uncertainties on a stock.
A protective put is taken by bullish investors worried about near-term uncertainties on a stock.
A Principal Protected Note (PPN) is a security created from a single option in such a way that the investor makes riskless profits from any gains in the value of the underlying portfolio.
Traders use Principal Protected Notes (PPNs) to hedge against losses while still providing room for potential gains. PPNs are used only in portfolios that provide income to the investor and are more attractive to risk-averse investors.
Assume that portfolio X comprises (i) a five-year bond with a face value of USD 1000 and (ii) a five-year call option on portfolio Y. Portfolio Y currently has a value of USD 1000, with a strike price of USD 1000. Assume also that the five-year interest rate is 10% and is compounded annually.
To benefit from PPNs, the holder of portfolio X should buy the bond now at \($1000(1+10\%)^{-5}=$620.92\).
After five years, using the $1000 face value of the bond, the holder of portfolio X can now purchase portfolio Y at a strike price of $1000.
By using PPNs, the holder of portfolio X hedges against any losses associated with a decline in the value of portfolio Y and still benefits from any increase in the value of portfolio Y.
The investor is able to use PPNs by: (i) giving up the interests that would have been earned on the bonds and (ii) not receiving any income from portfolio Y for five years.
Spread strategies involve either call options solely or put options solely. (Later on, we will see combination strategies, which involve both call and put options.)
Spread strategies include:
A bull spread is a bullish options strategy designed to take advantage of a moderate rise in the price of the underlying in the near term. In a bull call spread, a bullish trader buys a call with a lower strike price and simultaneously sells a call with a higher strike price. The premium received from the sale of the higher strike call subsidizes the premium paid for the purchase of the lower strike call.
Being bullish, the buyer of a bull call spread expects the underlying stock price to rise but remains below the short call’s strike.
Example of a bull call spread:
$$
\begin{array}{l|c}
\text{Buy 1 ABC 100 call at} & $5.50 \\ \hline
\text{Sell 1 ABC 105 call at} & $2.0 \\ \hline
\text{Net cost} & $3.50 \\
\end{array}
$$
The premium paid for the lower strike is higher than the premium received for, the higher strike because the lower strike has higher chances of being attained in the near term.
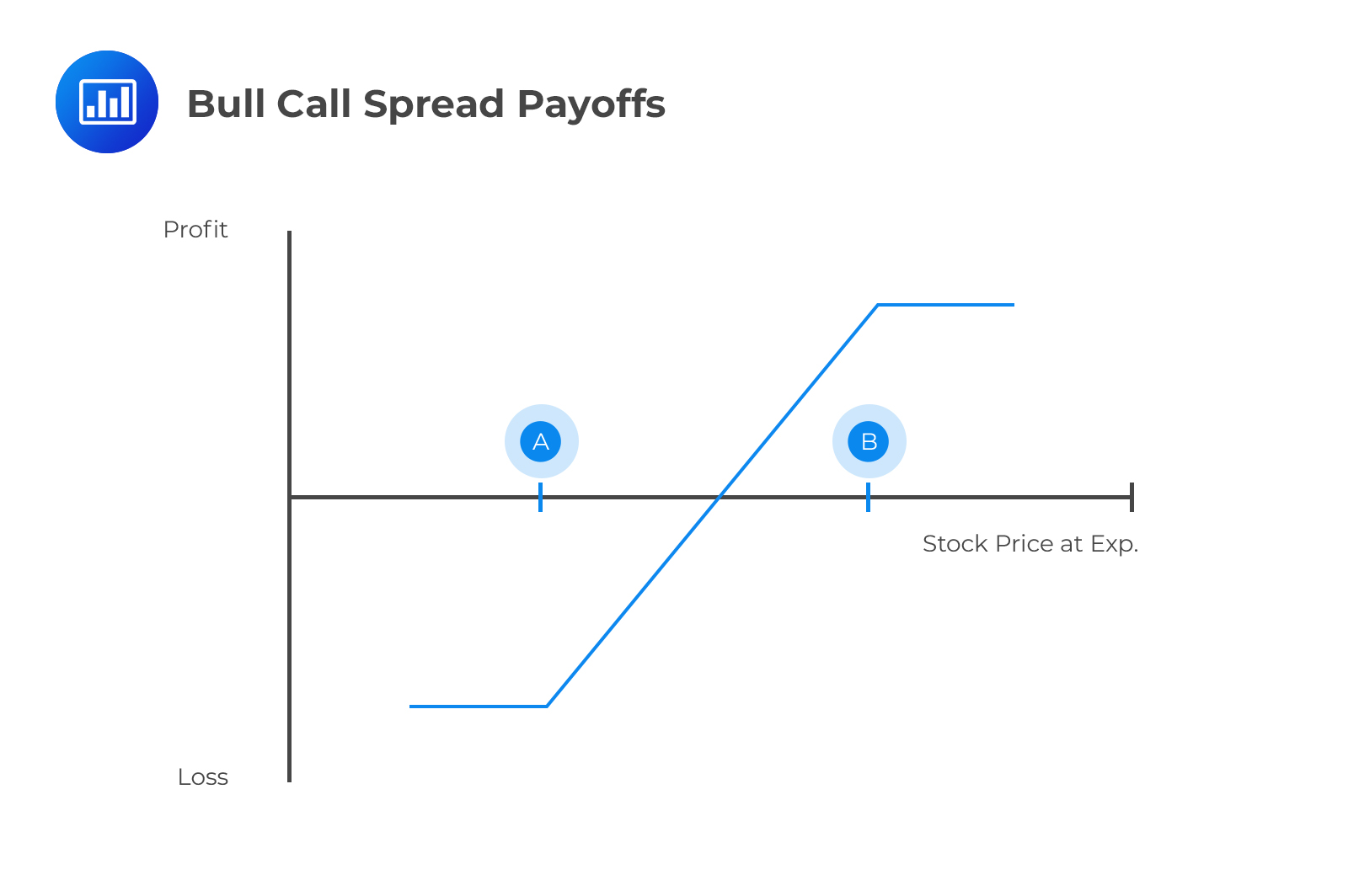 In a bull put spread, the bullish trader buys a put with a lower strike and simultaneously sells a put with a higher strike. The premium received from the sale of the higher strike put is higher than the premium paid for, the lower strike put. As such, the two positions generate a positive net income.
In a bull put spread, the bullish trader buys a put with a lower strike and simultaneously sells a put with a higher strike. The premium received from the sale of the higher strike put is higher than the premium paid for, the lower strike put. As such, the two positions generate a positive net income.
Example of a bull put spread:
$$\begin{array}{l|c}
\text{Sell 1 ABC 100 call at} & $3.50 \\ \hline
\text{Buy 1 ABC 95 call at} & \$1.8 \\ \hline
\text{Net benefit} & $1.7 \\
\end{array}$$
The maximum gain, maximum loss, and break-even point for a bull put spread strategy are as follows:<br>
Max profit = Net premium received
Max loss = Strike price of short put – strike price of long put – net premium received
Break-even point = Strike price of short put – net premium received
Note: In both call and put spreads, the expiration date, as well as the underlying asset, must be the same for both positions.
A bear spread is a bearish options strategy designed to take advantage of a moderate decline in the price of the underlying in the near term. A bear call spread consists of one long call with a higher strike price and one short call with a lower strike price. On the other hand, a bear put spread consists of one long put with a higher strike price and one short put with a lower strike price.
Note that bull spreads involve buying at a lower strike price and selling at a higher strike price. Bear spreads, on the other hand, involve buying at a higher strike price and selling at a lower strike price.
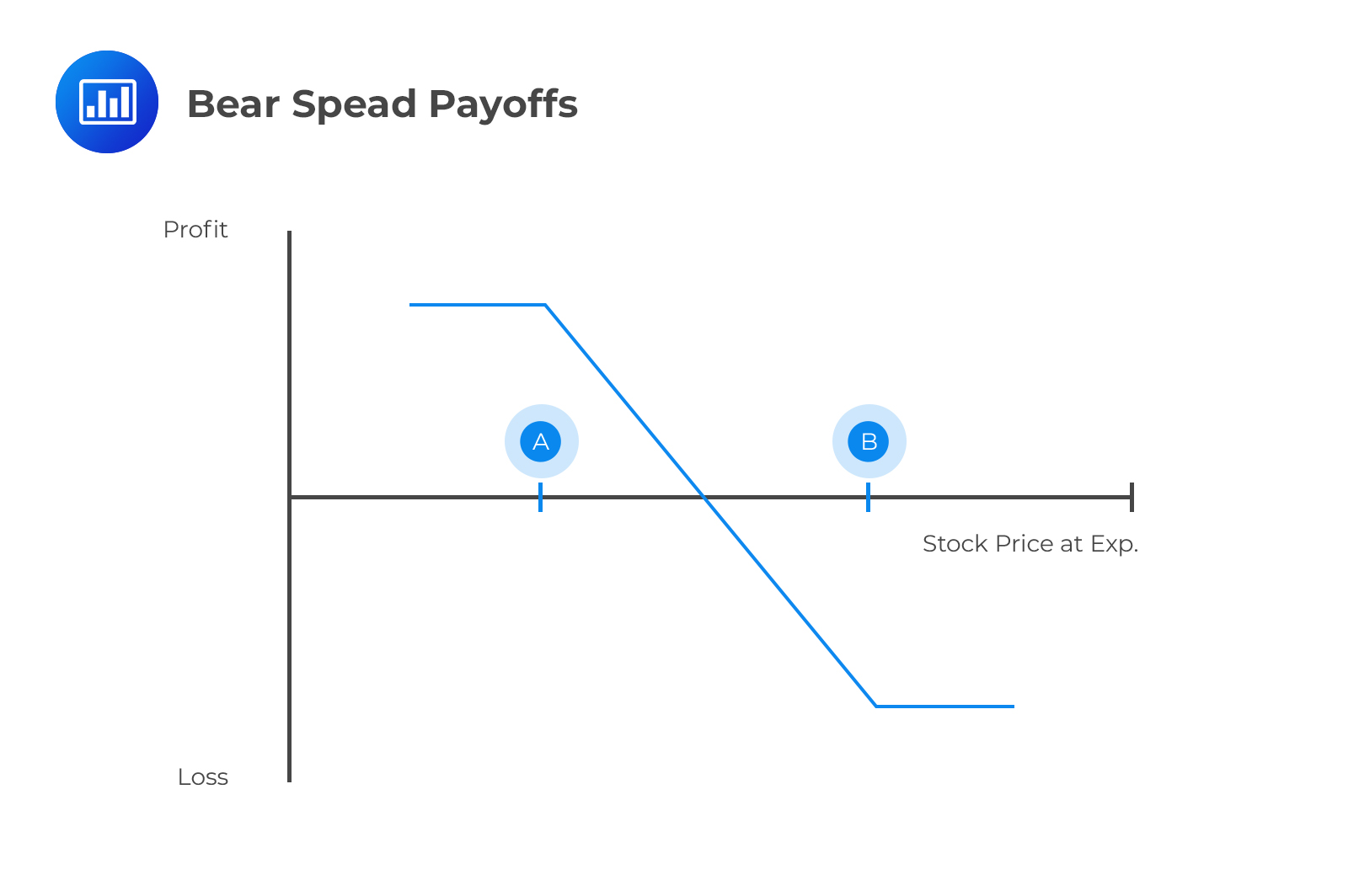
A box spread is a strategy created from a bull using call options and a bear spread using put options. The strike price and time to maturity of both bull and bear spreads should be the same.
A butterfly spread is a neutral, limited-risk strategy involving various bull spreads and bear spreads. The holder combines four options contracts that have the same expiry date at three strike price points, \(X_1\), \(X_3\), \(X_2=\frac{X_1+X_3}{2}\). Two option contracts are bought – one at a higher strike price and the other, at a lower strike price. Besides, two option contracts are sold at a strike price in between. A butterfly trader has reason to believe the underlying asset will not move too far away from the current price.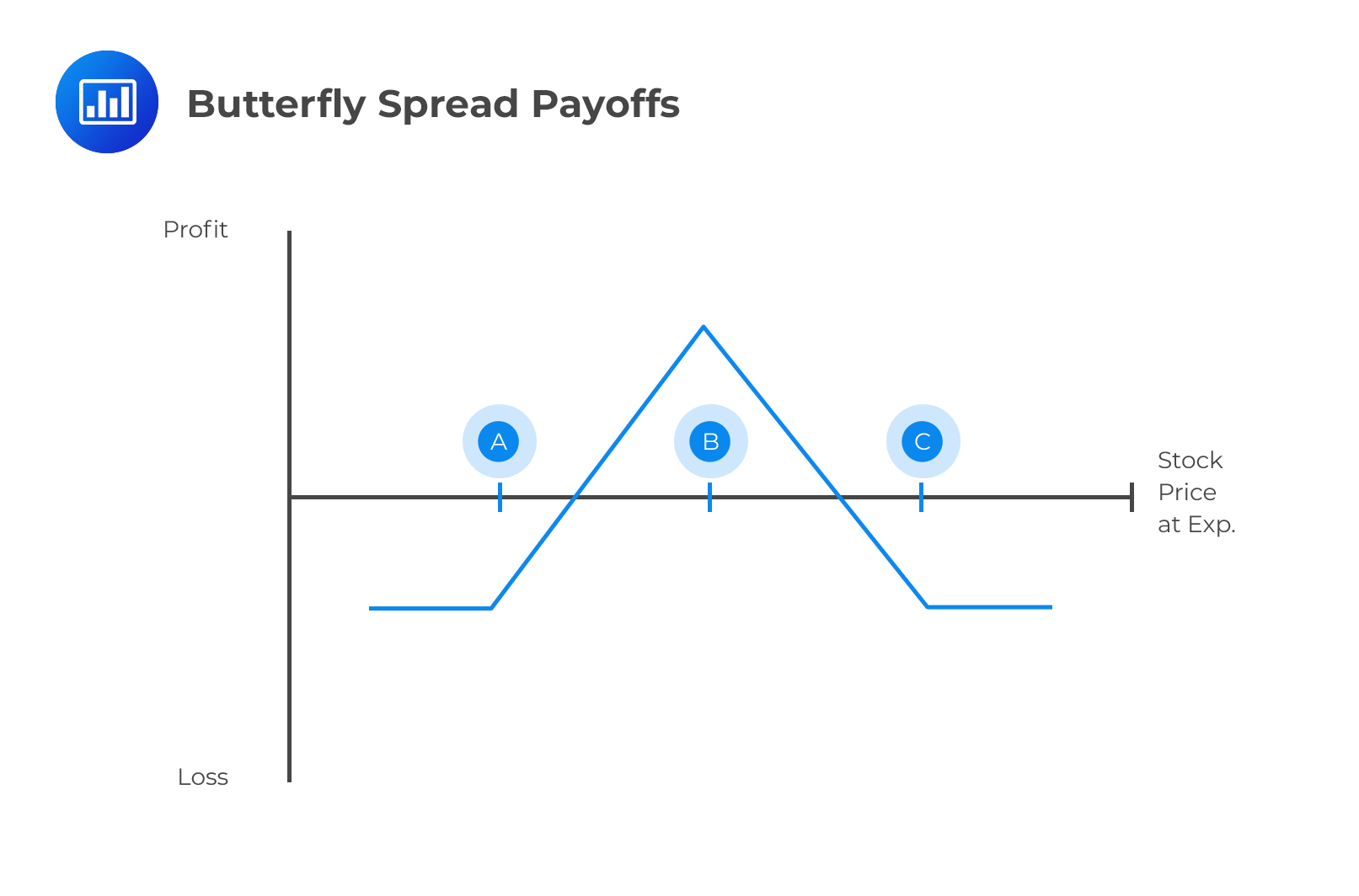
The table below shows the payoff from a butterfly spread created from calls, where \(S_T\) is the price of the asset.
$$\small{\begin{array}{l|c|c|c|l} {\textbf{Range}\\{\textbf{of} \quad\textbf{S}_\textbf{T}}}& {\textbf{Payoff from}\\ \textbf{Long Call}\\ \textbf{with Strike}\\{\textbf{Price}\quad\textbf{X}_\textbf{1}}} & {\textbf{Payoff from}\\ \textbf{Two Short Calls}\\ \textbf{with Strike}\\{\textbf{Price}\quad\textbf{X}_\textbf{2}}} &{ \textbf{Payoff from} \\ \textbf{Long Call}\\ \textbf{with Strike}\\ {\textbf{Price}\quad\textbf{X}_\textbf{3}} }& {\textbf{Total}\\ \textbf{Payoff}}\\ \hline {S_T≤X_1}& 0 & 0& 0 & 0 \\ {\text{X}_\text{1}<S_T≤X_2} & {S_T-X_1} & 0 & 0 &{S_T-X_1} \\
{X_2<S_T≤X_3} &{S_T-X_1} & {-2(S_T-X_2)}& 0 &{2X_2-X_1-S_T=X_3-S_T} \\
{S_T>X_3} &{S_T-X_1}&{-(S_T-X_2)}&{S_T-X_3}&{2X_2-X_1-X_3=0} \end{array}}$$
Similarly, the payoff from a butterfly spread created from put options can be shown in a table such as the one below:
$$\small{\begin{array}{l|c|c|c|l} {\textbf{Range of}\\{\textbf{S}_\textbf{T}}}& {\textbf{Payoff from}\\ \textbf{Long Put}\\ \textbf{with Strike}\\{\textbf{Price}\quad\textbf{X}_\textbf{1}} }& {\textbf{Payoff from}\\ \textbf{Two Short Puts}\\ \textbf{with Strike}\\{\textbf{price}\quad\textbf{X}_\textbf{2}}}& {\textbf{Payoff from}\\ \textbf{Long Put}\\ \textbf{with Strike}\\ {\textbf{Price}\quad\textbf{X}_\textbf{3}}} & {\textbf{Total}\\ \textbf{Payoff}}\\ \hline {S_T≤X_1}& {X_1-S_T}&-2(X_2-S_T) &X_3-S_T& 2X_2-X_1-X_3=0 \\{X_1<S_T≤X_2} & 0 & -2(X_2-S_T) &X_3-S_T &S_T+X_3-2X_2=S_T-X_1\\
{X_2<S_T≤X_3} &0 &0&X_3-S_T & X_3-S_T \\
{S_T>X_3} &0&0&{0} &{0} \end{array}}$$
A calendar spread is a trading strategy set up by simultaneously entering a long and short position on the same underlying asset and at the same strike price, but with different months to expiration. It’s a low-risk strategy that’s directionally neutral—the holder benefits from the passage of time or increase in the underlying’s implied volatility. As in a butterfly spread, the holder also believes the stock will have a narrow range of price changes. We have several categories of calendar spreads;
A diagonal spread works much like a calendar spread, but with a little difference; the options in a diagonal spread can have different strike prices in addition to different expirations.
Combination strategies involve both call and put options.
A straddle involves two transactions on the same security, with positions that offset one another. A long straddle is created by purchasing a call and a put with the same strike price and expiration. A short straddle is created by selling a call and a put with the same strike price and expiration. Straddles work much like butterfly and calendar spreads. Note, however, that the losses can be unlimited for short straddles. Long straddles can be appropriate when an investor expects significant movement in the stock price.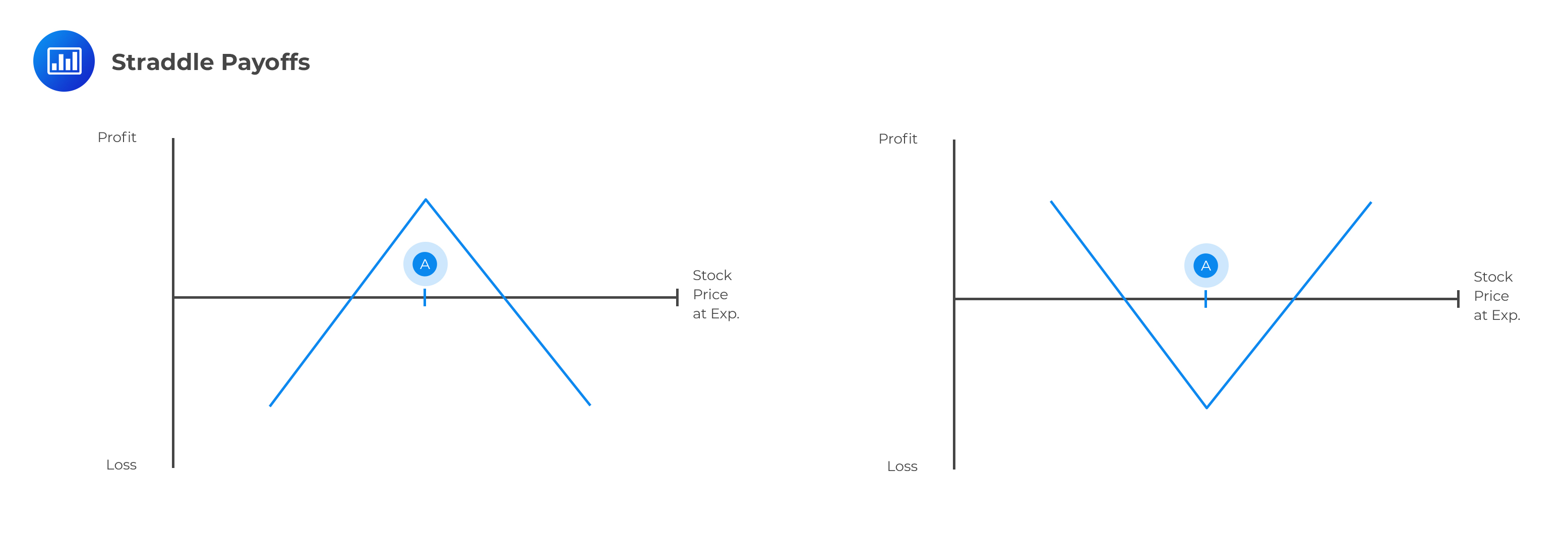 Example: Profits for a Long Straddle
Example: Profits for a Long Straddle
Assume that the price of a six-month European call option is $4.20, and that of a six-month European put option is $3.12. For there to be a profit using a long straddle strategy, the underlying asset price should move by at least $7.32 ($4.20+$3.12).
This implies that, for a strike price of $60, the trader will incur losses if the price of the asset at maturity is between $52.68 and $67.32.
The converse is also true. For a short straddle to be profitable, the stock price at expiration would need to be between $52.68 and $67.32.
Similar to the straddle, a long strangle consists of a long call and a long put option on the same underlying asset and with the same expiration date. In a strangle, however, the two options have different exercise prices. For there to be a profit in a strangle, the asset prices should move further as compared to a straddle. However, a strangle is less costly as compared to a straddle. 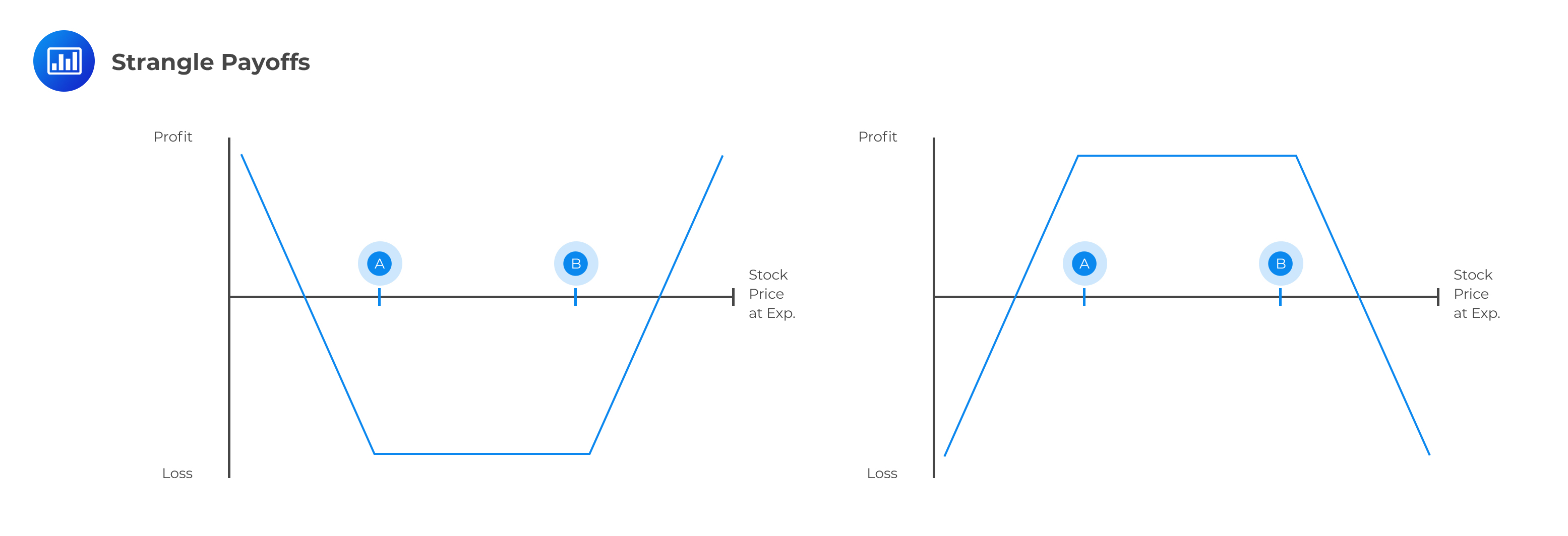
Assume that the strike price used for the put option is $60 and that used for the call option is $70. The cost of setting up the strangle might be buying a put for $4.20 (strike price of $60) and buying a call for $3.12 (strike price of $70), for a total of $7.32. Profits will be realized if the asset price at maturity is either greater than $77.32 (70+7.32) or less than $52.68 (60-7.32).
A strip is literally a long straddle, but the only difference is that a strip involves the purchase of two puts and one call(instead of one each as in straddle) with the same strike price and expiration. An investor enters a long-strip position when he expects a large move in a stock and the likelihood of a decrease in the stock price is higher than an increase.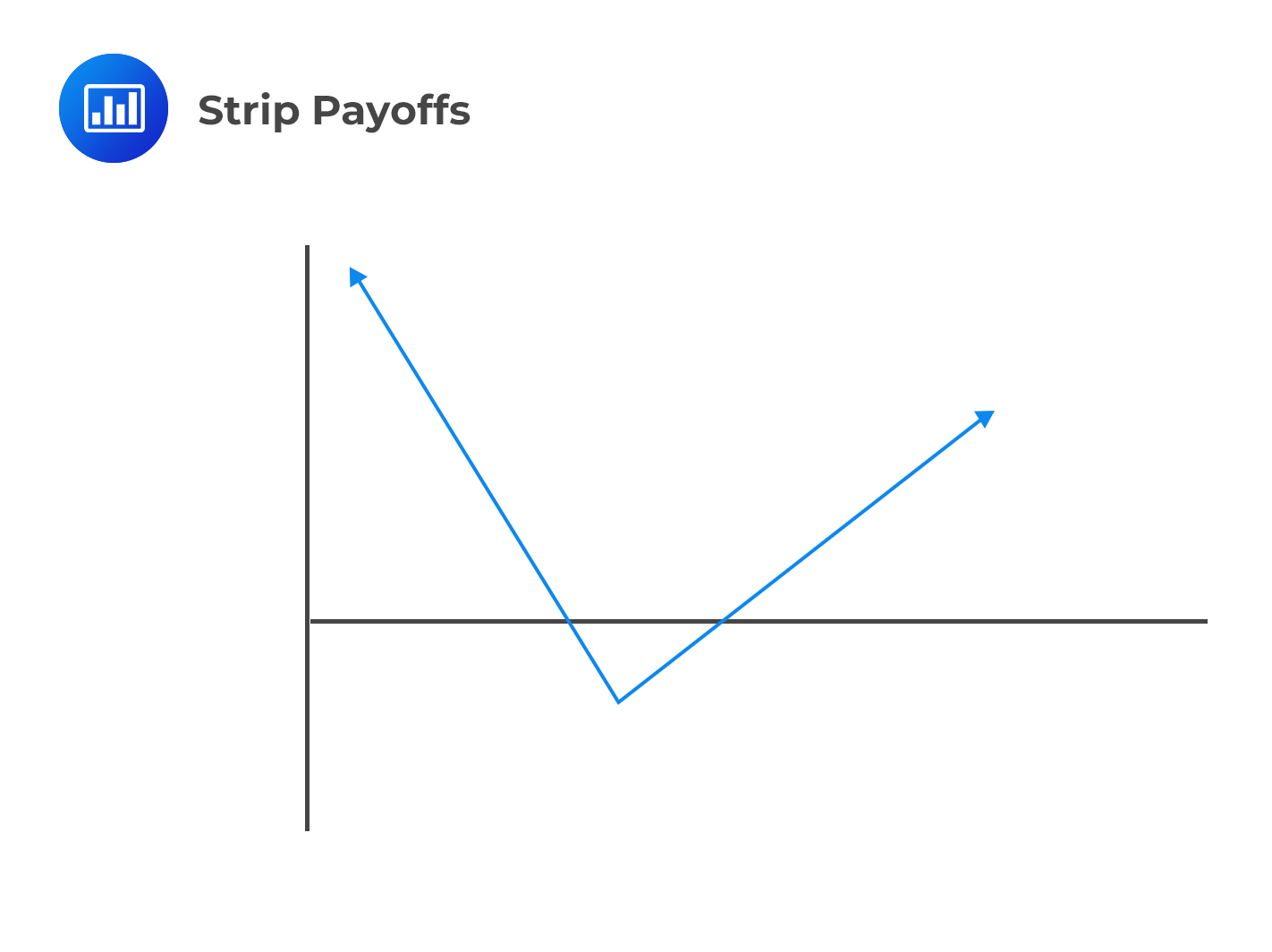
A long strap is a mirror image of a strip strategy. It consists of a long position in two calls and one put with the same exercise price and expiration date. An investor enters a long strap position when he expects large moves in a stock but considers an increase in the stock price more likely than a decrease.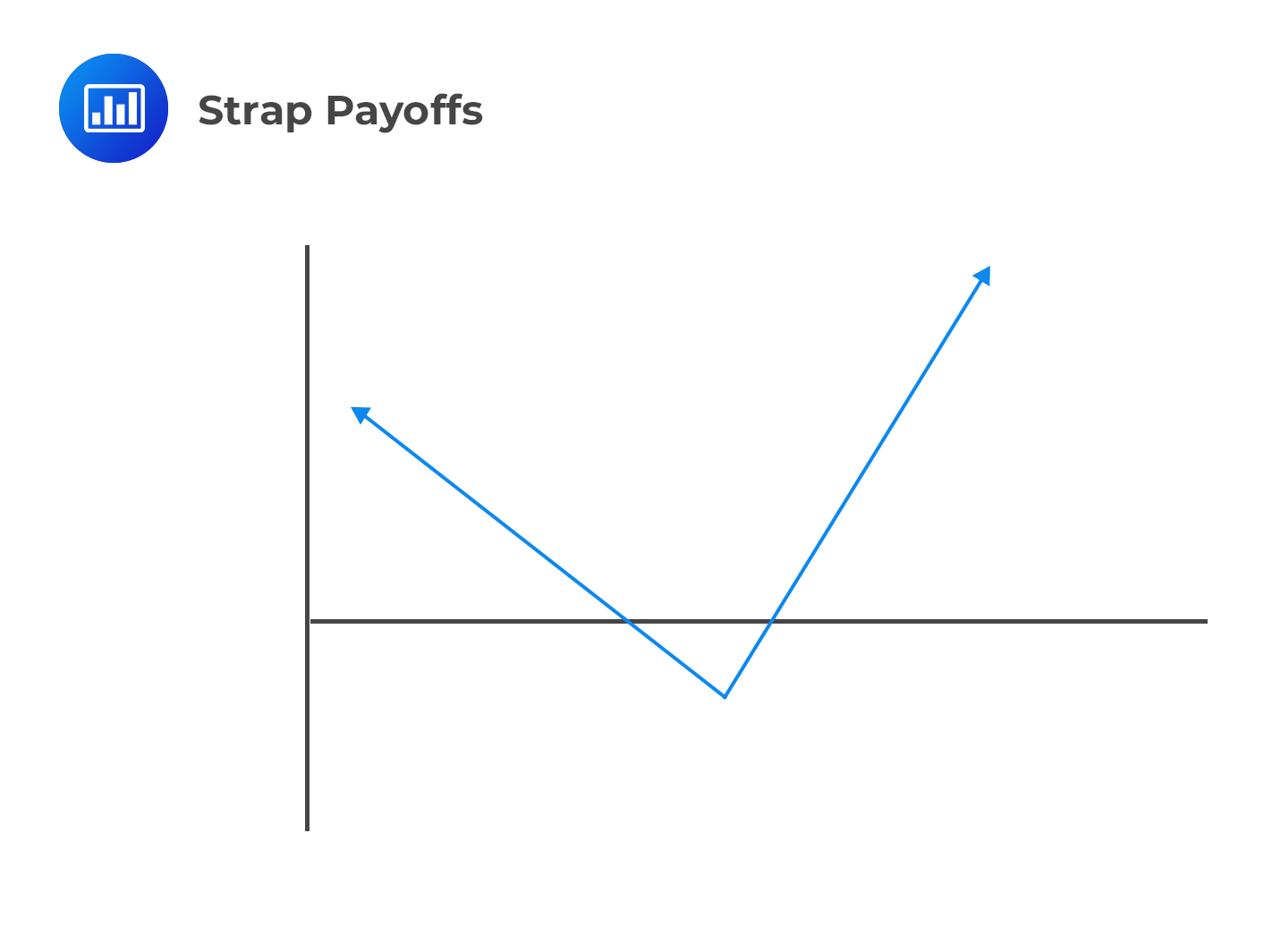
An interest rate cap is a type of interest rate derivative in which a buyer receives payments at the end of each period in which the interest rate exceeds the agreed strike price. The strike rate is also called the cap rate. For example, the buyer could receive payments when the rate exceeds LIBOR + 200bps.
On the other hand, an interest rate floor is a derivative contract in which a buyer receives payments at the end of periods in which the interest rate is below the agreed strike price. For example, the buyer could be entitled to a payment whenever the rate is below LIBOR + 50 bps.
Interest rate caps and floors provide protection against fluctuating interest rates.
Practice Questions
Question 1
Which of the following options trading strategies does not expose the party to unlimited losses?
A. Naked call
B. Covered call
C. Short strangle
D. Short straddle
The correct answer is B.
Options strategies that expose the party to unlimited losses include:
- Covered call
- Short straddle
- Short strangle.
Question 2
A trader wants to create a long strangle trading strategy with a strike prices of $50 for the call option and $40 for the put option. The prices of four-month European call and put options are $3.12 and $2.87, respectively. At maturity, the stock price has to be greater than which of the following to realize profits?
A. $50.
B. $34.01.
C. $53.12.
D. $55.99.
The correct answer is D.
The question is testing on the use of the long strangle trading strategy, a trading strategy that involves buying a call option with the higher strike price, and buying a put option with the lower strike price.
The strike price for the call (shown as B on the graph) = $50
The strike price for the put (shown as A on the graph) = $40
Cost of setting up the long strangle = $3.12 + $2.87 = $5.99
Upper price bound of the asset price at maturity = $50 + $5.99 = $55.99
Lower price bound of the asset price at maturity = $40 – $5.99 = $34.01